Funciones en Varias Variables

Hemos estudiado funciones que de forma explícita, dependen de sólo una variable y aunque también hemos estudiado funciones que definidas de forma implícita relacionan dos variables, no hemos estudiado formalmente funciones que dependan de dos o más variables.

También pudiera interesarte

El Espacio Cartesiano

Para ir más allá, recurrimos a una nueva variable $z$ que dependerá enteramente de las variables $x$ y $y$ . Notando que al definir una tercera variable, podemos hacer la representación gráfica de este tipo de funciones tomando en cuenta que hasta ahora hemos construido nuestros espacios intersectando ejes coordenados de forma perpendicular.

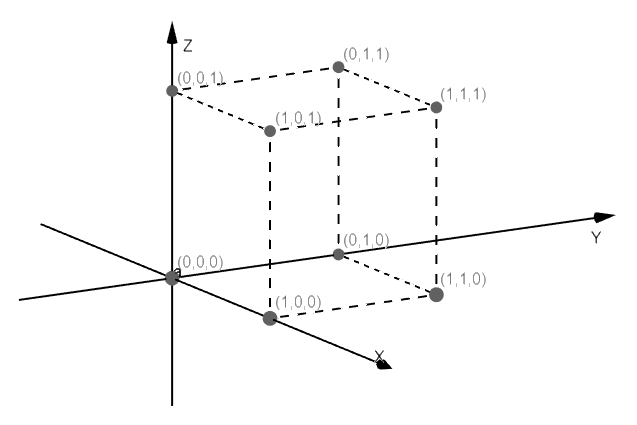
Esta vez no será diferente, así que considerando el plano cartesiano, intersectaremos a este en el origen con un eje perpendicular a los Ejes $Y$ y $X$ generando así el espacio cartesiano que consta de tres ejes coordenados $X$ , $Y$ y $Z$ :

Los planos en el espacio

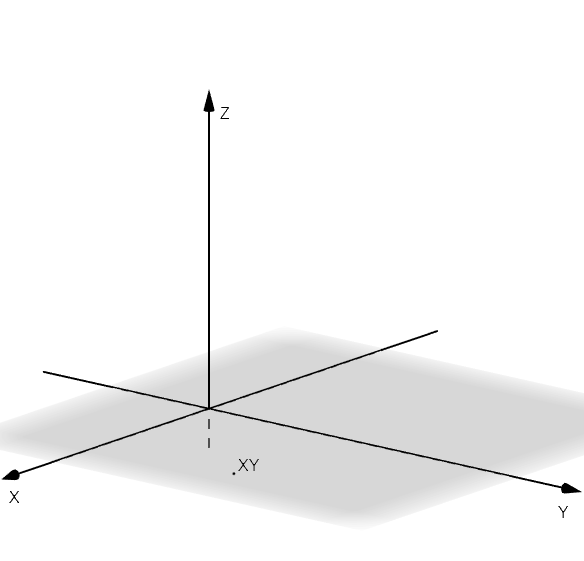
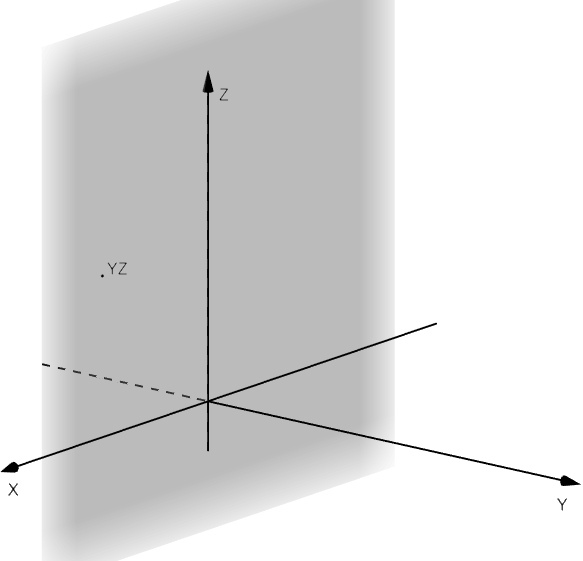
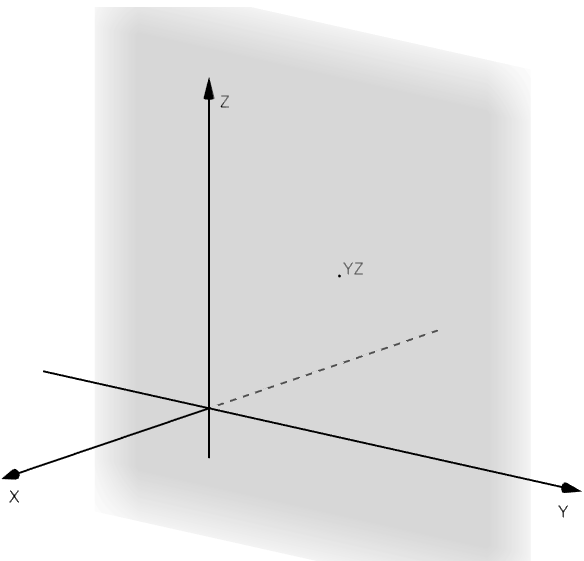
En este espacio podemos identificar tres planos principales, que se definen de la siguiente manera: El plano $XY$ que contiene todos los puntos de la forma $(x,y,0)$ , el plano $XZ$ que contiene todos los puntos de la forma $(x,0,z)$ y el plano $YZ$ que contiene todos los puntos de la forma $(0,y,z)$ .

Funciones en el espacio

De esta forma, podemos generalizar la definición de función que hasta ahora conocemos. Formalmente, si $R$ una región en el plano $XY$ , entonces definimos una función $f : R \to \mathbb{R}$ como una regla de correspondencia que corresponde a cada par ordenado de la región $R$ con un único número real $z = f(x,y)$ .

A este tipo de funciones las llamaremos funciones de dos variables. Evaluamos este tipo de funciones sustituyendo los valores de $x$ y $y$ por sus valores correspondientes, y así, calculamos sus imágenes. Veamos algunos ejemplos para entender como calcular imágenes.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ejemplos

Ejemplo 1

Evalúe la función $f(x,y) = x^2 + y^2$ en el punto $(3,-1)$ . Entonces sustituimos $x$ por $3$ y $y$ por $-1$ de la siguiente forma:

$f(3,-1) = (3)^2 + (-1)^2= 9 + 1= 10$

Ejemplo 2

Evalúe la función $f(x,y) = \sqrt{x+20} + \textit{\Large e}^{2x-8} + 20$ en el punto $(-13,4)$ . Entonces sustituimos $x$ por $-13$ y $y$ por $4$ de la siguiente forma:

$f(-13,4) = \sqrt{-13+20} + \textit{\Large e}^{2(4)-8} + 20 = \sqrt{9} + \textit{\Large e}^{0} + 20 = 3 + 1 + 20 = 24$

Ejemplo 3

Evalúe la función $f(x,y) = \frac{7}{x+y}$ en el punto $(18,10)$ . Entonces sustituimos $x$ por $18$ y $y$ por $10$ de la siguiente forma:

$f(18,10) = \frac{7}{18+10} = \frac{7}{28} = \frac{1}{4}$

Gráfica de funciones en el espacio

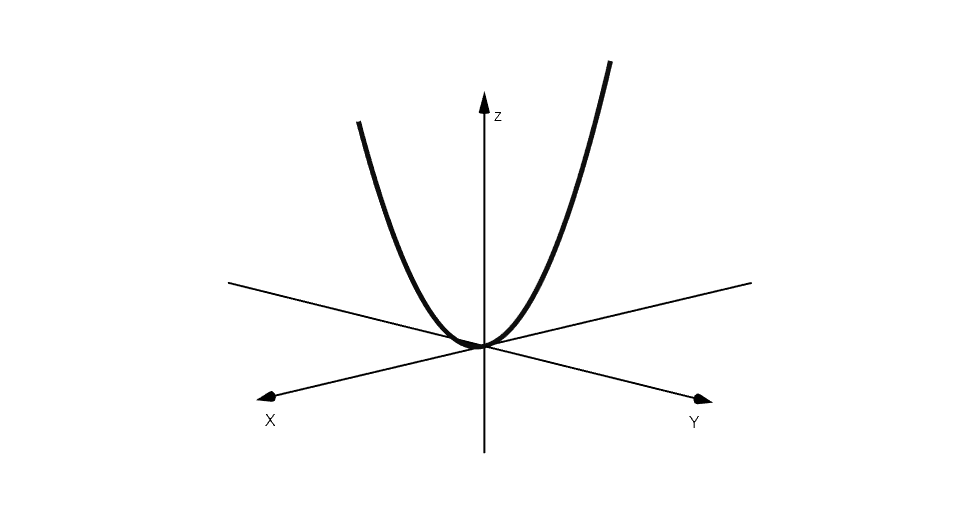
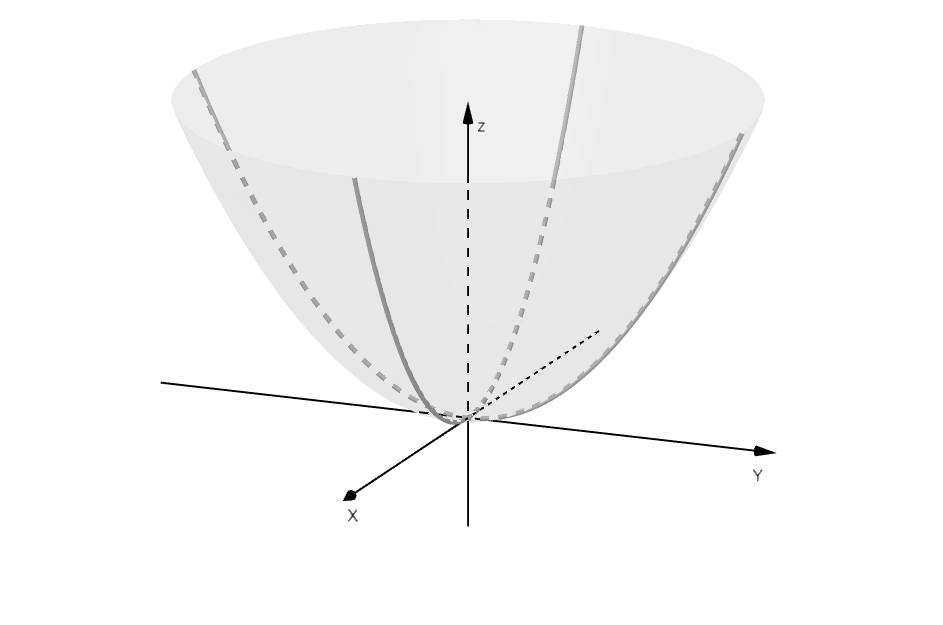
Existen diversas técnicas para graficar este tipo de funciones definidas en varias variables, una de ellas es proyectar las curvas que esta define en cada plano.

Por ejemplo, si consideramos nuevamente la función $f(x,y)=x^2+y^2$ , podemos ver su proyección en el plano $XZ$ considerando $y=0$ , de esta forma la función se puede escribir de la siguiente forma: