A medida que los desarrollos matemáticos se hacen más complejos es necesario introducir herramientas que nos permitan reescribirlos de forma sencilla y entendible. La herramienta que introducimos a continuación permite encapsular varios elementos en una sola estructura y al definir operaciones sobre estas estructuras, podemos establecer relaciones con otro tipo de estructuras matemáticas.
También pudiera interesarte
Filas, Columnas y Tamaño de una Matriz
Definimos una matriz como un arreglo rectangular de números reales, que encerramos entre paréntesis , dispuestos en filas y columnas de la siguiente manera:


Los números que componen la matriz serán llamados elementos o entradas de la matriz, diremos que las filas son los arreglos horizontales y los contaremos de arriba hacia abajo, por otra parte, diremos que las columnas son los arreglos verticales y los contaremos de izquierda a derecha. En este caso, la matriz tiene tres filas y cuatro columnas, es por esto que diremos que es una matriz de tamaño .
Veamos algunos ejemplos de matrices de distintos tamaños para entender la idea sobre como contar las filas y las columnas de una matriz.
Ejemplos
Ejemplo 1

es una matriz de tamaño .
Ejemplo 2

es una matriz de tamaño .
Ejemplo 3

es una matriz de tamaño .
Ejemplo 4

es una matriz de tamaño .
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Elementos de una Matriz
Una vez que hemos identificado cada fila y cada columna, podemos identificar cada uno de los elementos de una matriz considerando la fila y la columna en que se encuentren, por ejemplo,
Ejemplos
Ejemplo 5
está en la fila
y columna
.

Ejemplo 6
está en la fila
y columna
.

Ejemplo 7
está en la fila
y columna
.

Ejemplo 8
está en la fila
y columna
.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Diagonal de una Matriz
Usualmente denotaremos las matrices con letras mayúsculas () y a cada elemento de la matriz lo denotamos con letras mayúsculas (
). Así, de forma general, diremos que una matriz
de tamaño
se denota de la siguiente manera:

Donde denota el elemento que se encuentra en la fila
y la columna
de la matriz A (este elemento también se puede denotar con
). Todos los elementos de la forma
son los elementos de la diagonal de
, veamos algunos ejemplos para identificar estos elementos con mayor facilidad.
Ejemplos
Ejemplo 9
En este caso y
son los elementos de la diagonal.
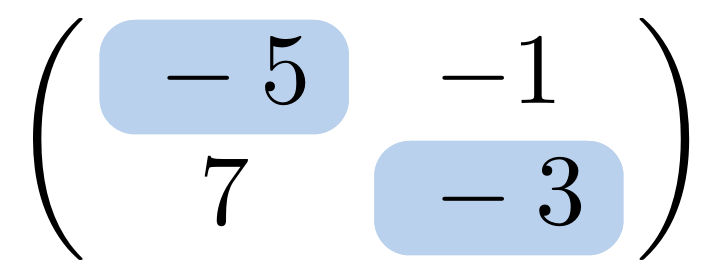
Ejemplo 10
En este caso ,
y
son los elementos de la diagonal.

Ejemplo 11
En este caso es el único elemento de la diagonal.
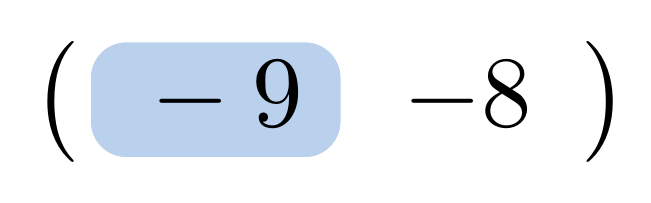
Ejemplo 12
En este caso y
son los elementos de la diagonal.


[…] Definición de Matriz. […]
Me gustaMe gusta