Al trabajar con matrices, nos toparemos de forma recurrente con algunas matrices que tienen ciertas características muy particulares, a este tipo de matrices se les conocen como matrices especiales y a continuación las listaremos junto con algunas de sus propiedades respecto a las operaciones con otras matrices y su determinante.
También pudiera interesarte
Matriz Cero
La Matriz Cero es una matriz cuadrada tal que cada uno de sus elementos es igual a cero, se denota con un cero en negrita para diferenciarla del escalar cero.Formalmente decimos que
para todo
y la expresamos de la siguiente manera:
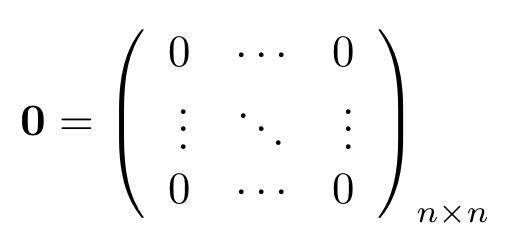
- Si
es una matriz, entonces
.
- Si
es una matriz, entonces
.
- Su determinante es igual a cero, es decir,
.
Las siguientes matrices son matrices cero del tamaño correspondiente:
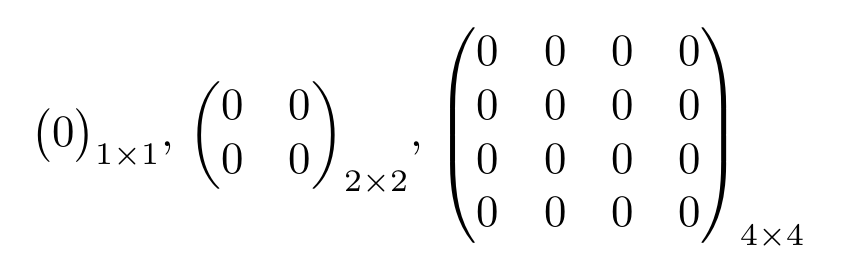
Matriz Identidad
La Matriz Identidad es una matriz cuadrada tal que cada uno de sus elementos es igual a cero, salvo los elementos de su diagonal que son todos iguales a uno, se denota con . Formalmente decimos que
para todo
y
para todo
, y la expresamos de la siguiente manera:
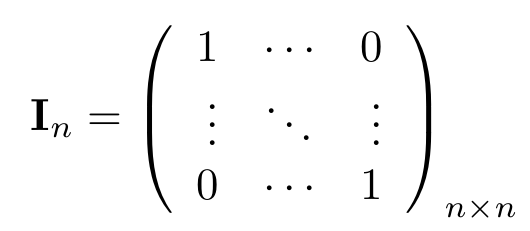
- Si
es una matriz, entonces
.
- Su determinante es igual a uno, es decir,
.
Las siguientes matrices son matrices identidad del tamaño correspondiente:
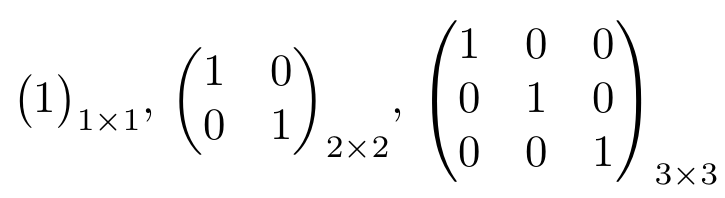
Matriz Diagonal
Una matriz cuadrada es Matriz Diagonal si cada uno de sus elementos fuera de la diagonal es igual a cero, en ocasiones se denotan con . Formalmente decimos que
para todo
y la expresamos de la siguiente manera:
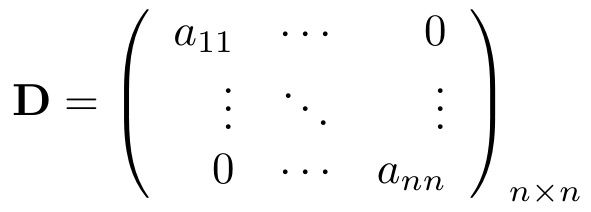
- Su determinante es el producto de todos los elementos de su diagonal, es decir,
.
Las siguientes matrices son matrices diagonales del tamaño correspondiente:
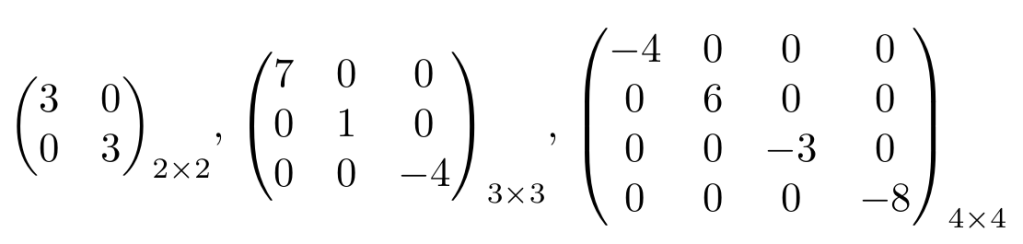
También podemos definir matrices diagonales que no sean cuadradas pero en esos casos, no podemos calcular su determinante.
Matriz Triangular Superior
Una matriz cuadrada es una Matriz Triangular Superior si todos los elementos que están por debajo de la diagonal, son iguales a cero, en ocasiones se denotan con . Formalmente decimos que
si
y la expresamos de la siguiente manera:
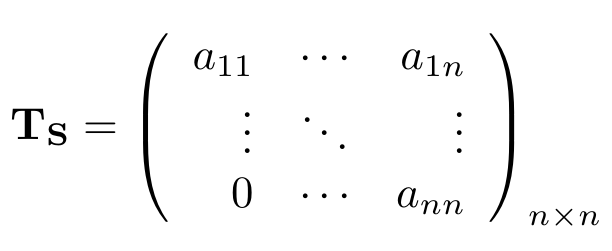
Su determinante es el producto de todos los elementos de su diagonal, es decir, .
Las siguientes matrices son matrices diagonales del tamaño correspondiente:
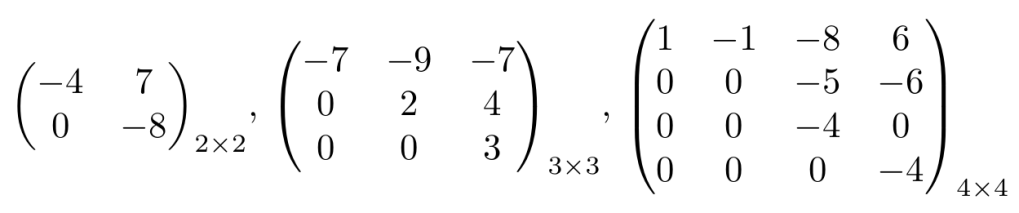
También podemos definir matrices triangulares superiores que no sean cuadradas pero en esos casos, no podemos calcular su determinante.
Matriz Triangular Inferior
Una matriz cuadrada es una Matriz Triangular Inferior si todos los elementos que están por encima de la diagonal, son iguales a cero, en ocasiones se denotan con . Formalmente decimos que
si
y la expresamos de la siguiente manera:
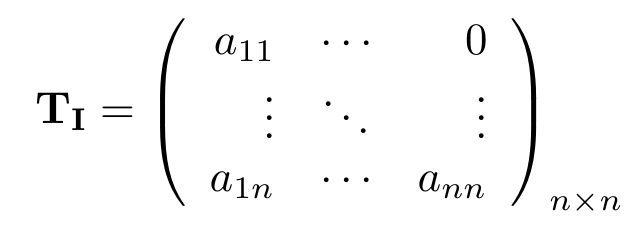
- Su determinante es el producto de todos los elementos de su diagonal, es decir,
Las siguientes matrices son matrices diagonales del tamaño correspondiente:
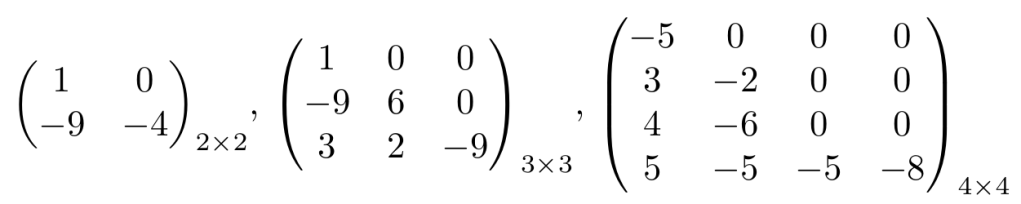
También podemos definir matrices triangulares inferiores que no sean cuadradas pero en esos casos, no podemos calcular su determinante.


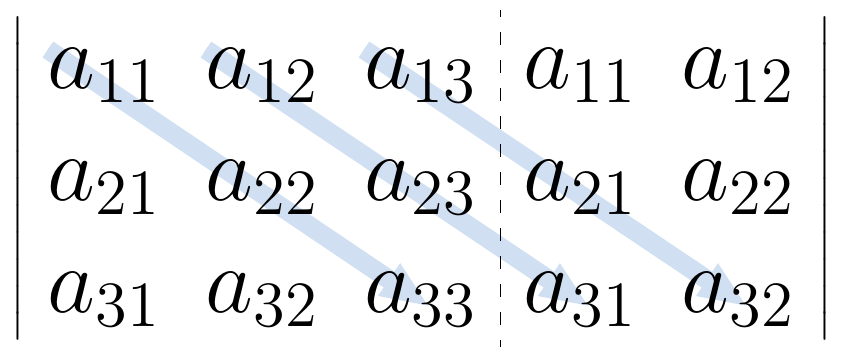
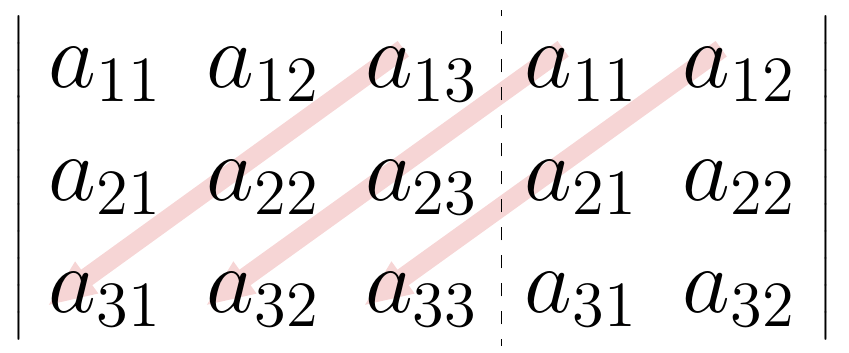
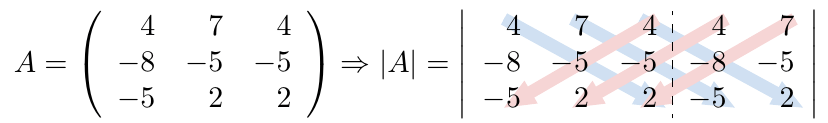
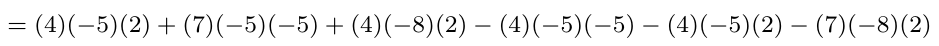
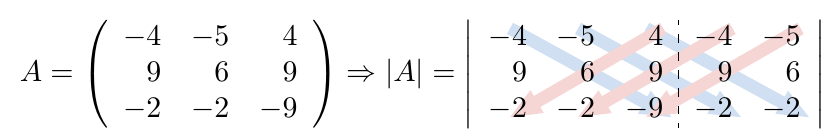
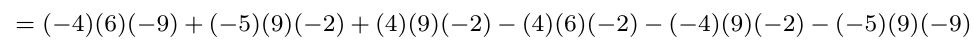
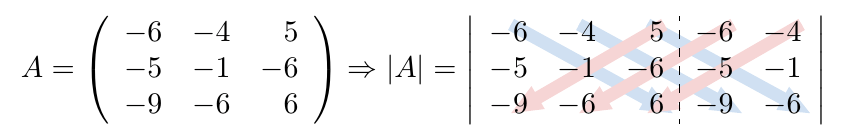
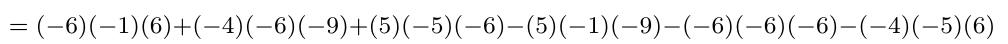
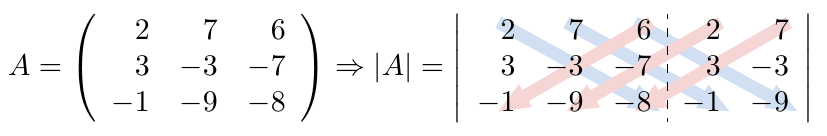
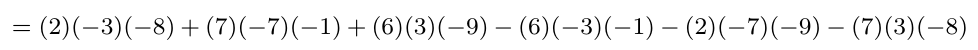
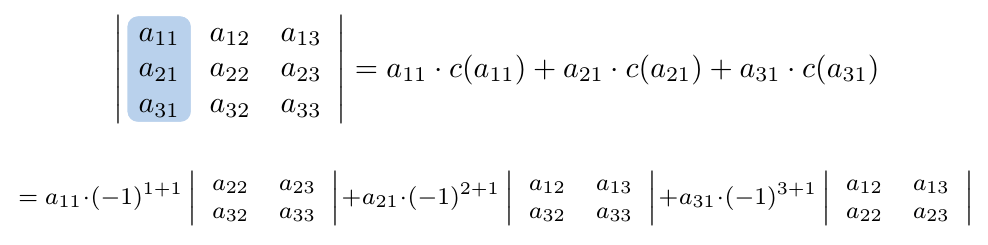
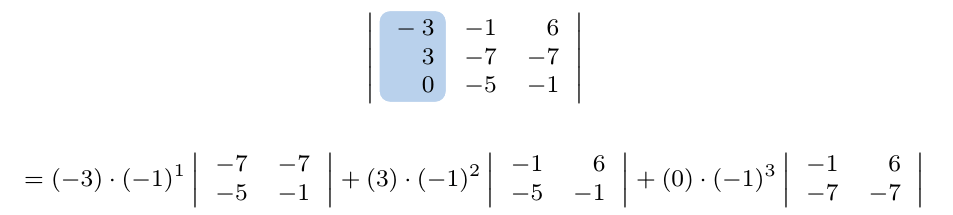

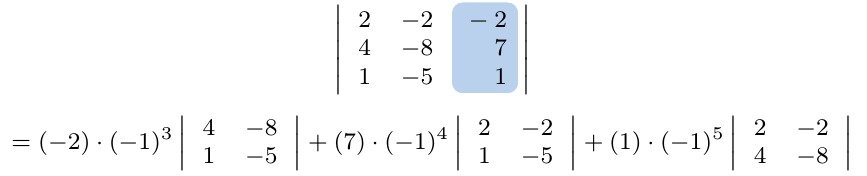
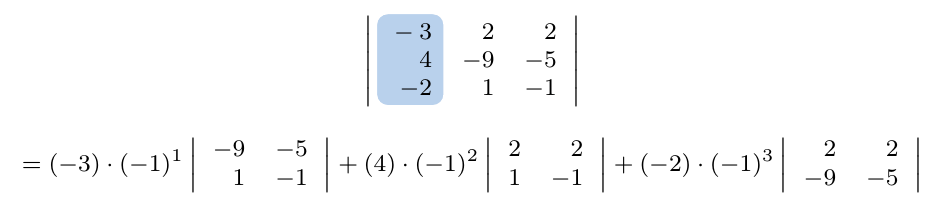
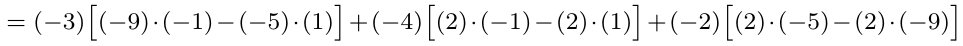

















Debe estar conectado para enviar un comentario.