- Intercambio de filas de una matriz
- Suma de filas de una matriz
- Multiplicar una fila de una matriz por un escalar
- Sumar una fila de una matriz multiplicada por un escalar
- Matrices equivalentes por filas
- Intercambio de columnas de una matriz
- Suma de columnas de una matriz
- Multiplicar una columna de una matriz por un escalar
- Sumar una columna de una matriz multiplicada por un escalar
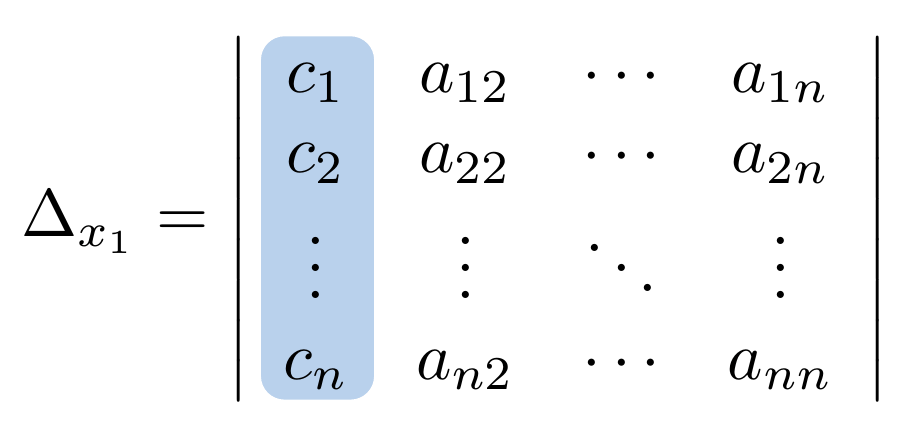
Si bien hemos podido definir operaciones entre matrices, es posible definir operaciones entre y sobre las filas de una matriz y de igual manera, es posible definir operaciones entre y sobre las columnas de una matriz. Veremos además, que al aplicar estas operaciones, podemos deducir el determinante de la nueva matriz a partir de la matriz original.
También pudiera interesarte
Operaciones elementales por fila
Veamos a continuación cuales son las operaciones que podemos definir sobre y entre las filas de una matriz.
Intercambio de filas de una matriz
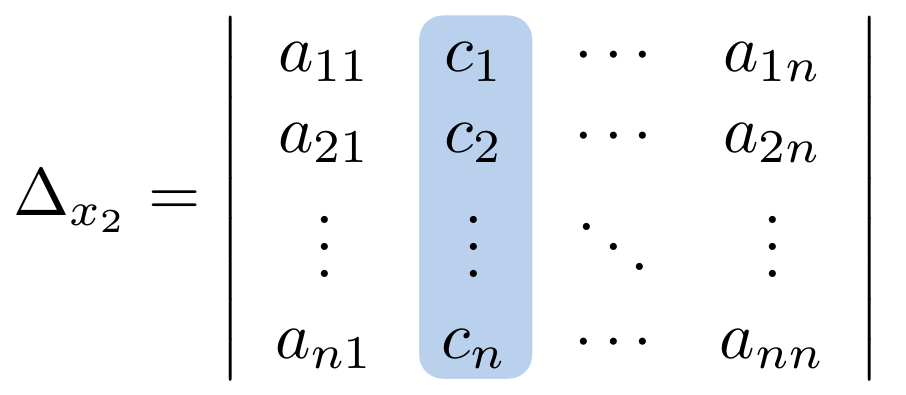
Si y
son dos filas de una matriz
de tamaño
, tales que
, denotamos el intercambio de estas dos filas usando la notación
y la expresamos de la siguiente manera:

Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 1
Consideremos una matriz de tamaño e intercambiemos la fila
por la fila
, entonces,
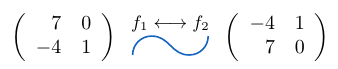
Ejemplo 2
Consideremos una matriz de tamaño e intercambiemos la fila
por la fila
, entonces,

Ejemplo 3
Consideremos una matriz de tamaño e intercambiemos la fila
por la fila
, entonces,

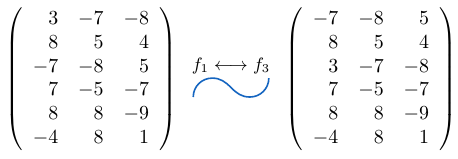
Ejemplo 4
Consideremos una matriz de tamaño e intercambiemos la fila
por la fila
, entonces,
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Suma de filas de una matriz
Si y
son dos filas de una matriz
de tamaño
, tales que
. Podemos considerar la fila
y sumarle la fila
, es decir, sumar los términos correspondientes, para esto usamos la notación
y la expresamos de la siguiente manera:

Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 5
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
, entonces,
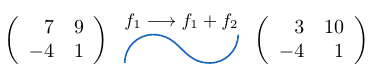
Ejemplo 6
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
, entonces,
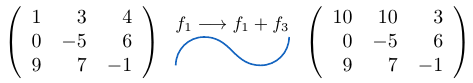
Ejemplo 7
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
, entonces,
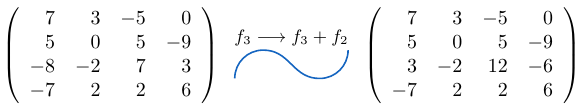
Fe de erratas: El elemento resultante es igual a
.
Ejemplo 8
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
, entonces,
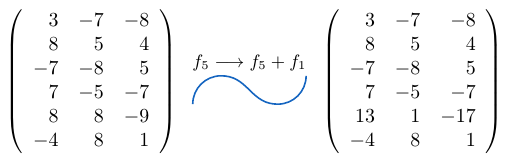
Fe de erratas: El elemento resultante es igual a
.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Multiplicar una fila de una matriz por un escalar
Si es una fila de una matriz
de tamaño
. Podemos considerar la fila
y multiplicarla por un escalar
, para esto usamos la notación
y la expresamos de la siguiente manera:
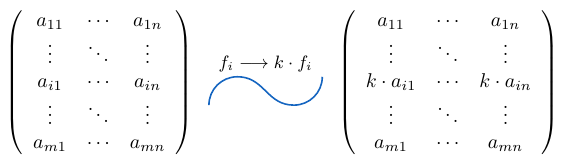
Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 9
Consideremos una matriz de tamaño y multipliquemos la fila
por el escalar
, entonces,
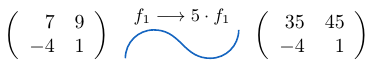
Ejemplo 10
Consideremos una matriz de tamaño y multipliquemos la fila
por el escalar
, entonces,
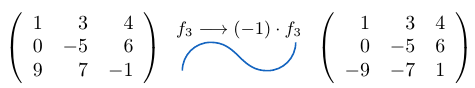
Ejemplo 11
Consideremos una matriz de tamaño y multipliquemos la fila
por el escalar
, entonces,

Ejemplo 12
Consideremos una matriz de tamaño y multipliquemos la fila
por el escalar
, entonces,
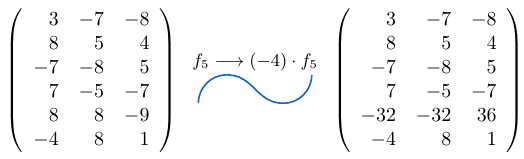
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
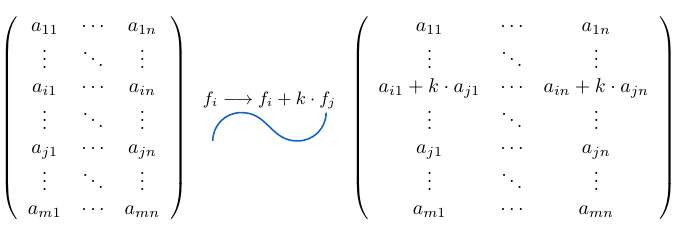
Sumar una fila de una matriz multiplicada por un escalar
Finalmente, veremos una operación elemental que de cierta forma mezcla efectúa varias operaciones al mismo tiempo. Si y
son dos filas de una matriz
de tamaño
, tales que
. Podemos considerar la fila
y sumarle la fila
multiplicada por un escalar
, para esto usamos la notación
y la expresamos de la siguiente manera:
Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 13
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
multiplicada por
, entonces,
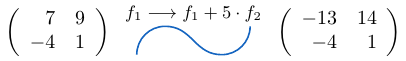
Ejemplo 14
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
multiplicada por
, entonces,
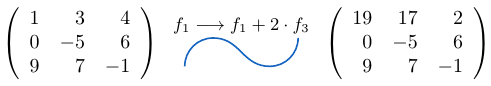
Ejemplo 15
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
multiplicada por
, entonces,
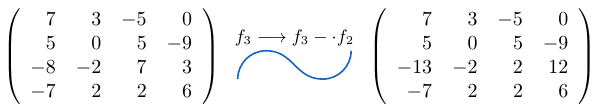
Notemos que en este caso estamos definiendo la resta de filas de una matriz.
Ejemplo 16
Consideremos una matriz de tamaño y a la fila
le sumamos la fila
multiplicada por
, entonces,
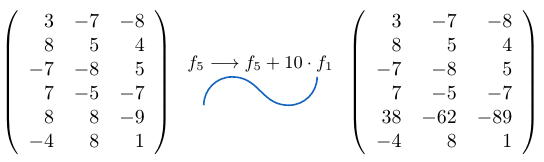
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Matrices equivalentes por filas
Una vez que se ha hecho una operación elemental por fila a una matriz, se pueden seguir haciendo operaciones elementales por fila a las matrices resultantes de forma sucesiva. Diremos que si una matriz se obtiene a partir de una matriz
a través de una sucesión finita de operaciones elementales por filas, entonces diremos que las matrices
y
son matrices equivalentes por filas y esta relación la denotaremos por
Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplo
Consideremos una matriz de tamaño , haciendo operaciones elementales por fila de forma sucesiva, veamos que esta es equivalente a la matriz identidad
.
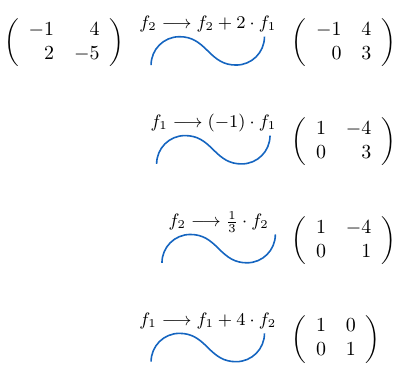
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Operaciones elementales por columna
Veamos a continuación cuales son las operaciones que podemos definir sobre y entre las filas de una matriz.
Intercambio de columnas de una matriz
Si y
son dos columnas de una matriz
de tamaño
, tales que
, denotamos el intercambio de estas dos columnas usando la notación
y la expresamos de la siguiente manera:
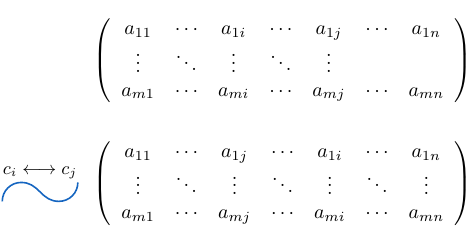
Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 17
Consideremos una matriz de tamaño e intercambiemos la columna
por la columna
, entonces,
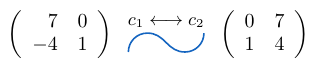
Ejemplo 18
Consideremos una matriz de tamaño e intercambiemos la columna
por la columna
, entonces,

Ejemplo 19
Consideremos una matriz de tamaño e intercambiemos la columna
por la columna
, entonces,
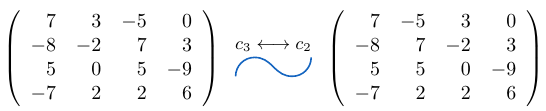
Ejemplo 20
Consideremos una matriz de tamaño e intercambiemos la columna
por la columna
, entonces,

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Suma de columnas de una matriz
Si y
son dos columnas de una matriz
de tamaño
, tales que
. Podemos considerar la columna
y sumarle la columna
, es decir, sumar los términos correspondientes, para esto usamos la notación
y la expresamos de la siguiente manera:
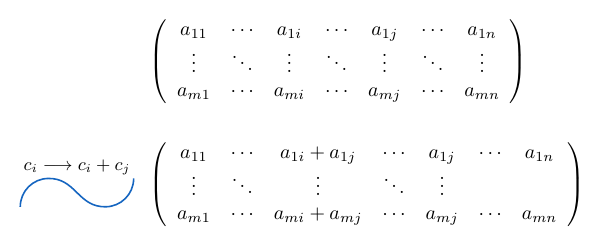
Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 21
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
, entonces,
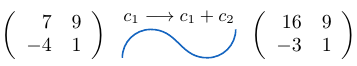
Ejemplo 22
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
, entonces,
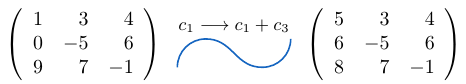
Ejemplo 23
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
, entonces,

Ejemplo 24
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
, entonces,

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Multiplicar una columna de una matriz por un escalar
Si es una columna de una matriz
de tamaño
. Podemos considerar la columna
y multiplicarla por un escalar
, para esto usamos la notación
y la expresamos de la siguiente manera:
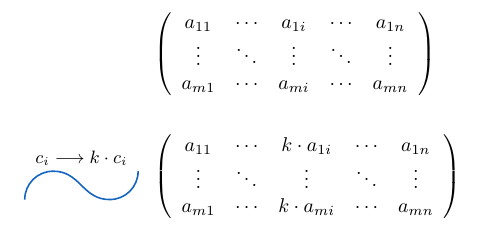
Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 25
Consideremos una matriz de tamaño y multipliquemos la columna
por el escalar
, entonces,

Ejemplo 26
Consideremos una matriz de tamaño y multipliquemos la columna
por el escalar
, entonces,

Ejemplo 27
Consideremos una matriz de tamaño y multipliquemos la columna
por el escalar
, entonces,

Ejemplo 28
Consideremos una matriz de tamaño y multipliquemos la columna
por el escalar
, entonces,
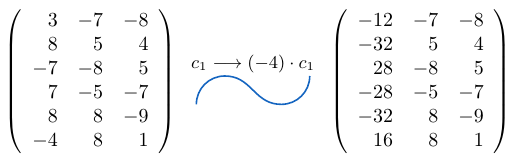
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Sumar una columna de una matriz multiplicada por un escalar
Finalmente, veremos una operación elemental que de cierta forma mezcla efectúa varias operaciones al mismo tiempo. Si y
son dos columnas de una matriz
de tamaño
, tales que
. Podemos considerar la columna
y sumarle la columna
multiplicada por un escalar
, para esto usamos la notación
y la expresamos de la siguiente manera:
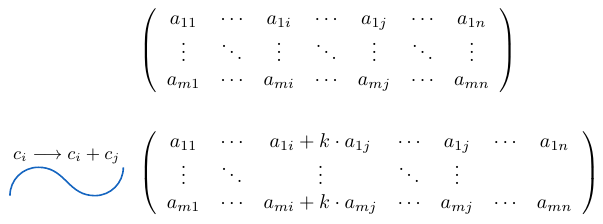
Veamos algunos ejemplos para ilustrar esta idea con más claridad.
Ejemplos
Ejemplo 29
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
multiplicada por
, entonces,
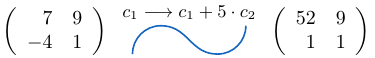
Ejemplo 30
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
multiplicada por
, entonces,
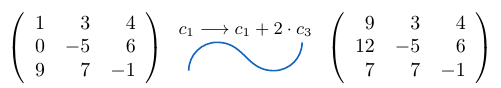
Ejemplo 31
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
multiplicada por
, entonces,

Notemos que en este caso estamos definiendo la resta de columnas.
Ejemplo 32
Consideremos una matriz de tamaño y a la columna
le sumamos la columna
multiplicada por
, entonces,
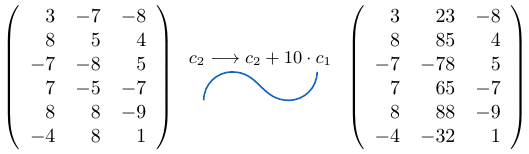

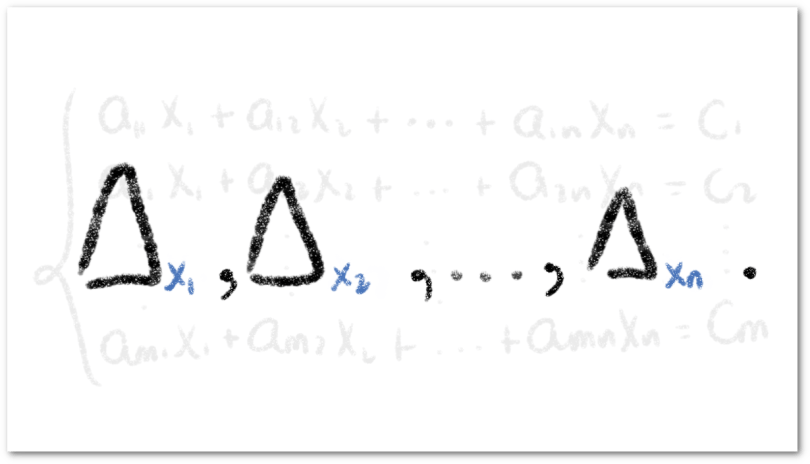
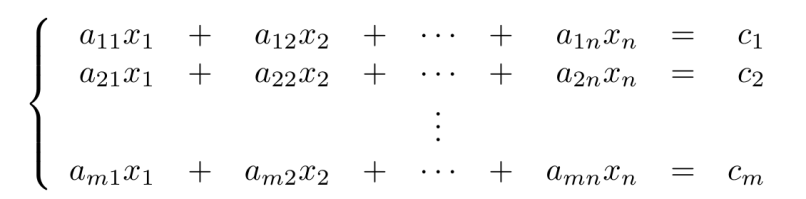
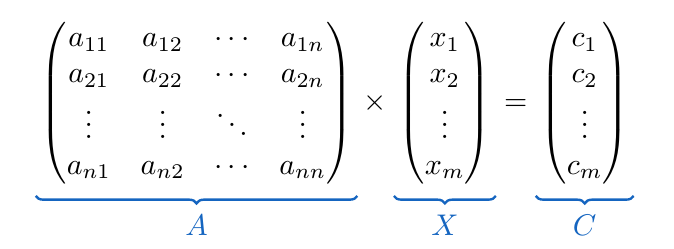
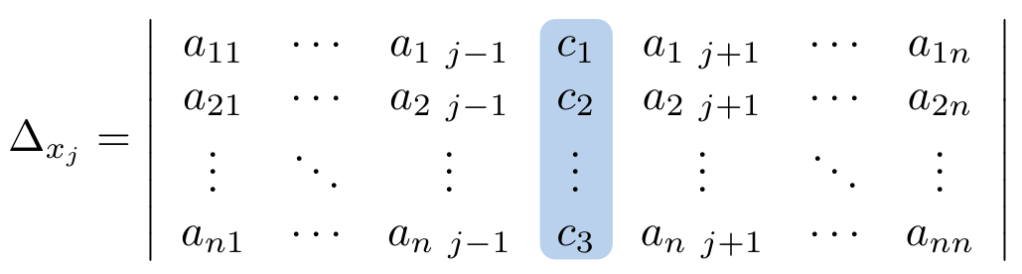
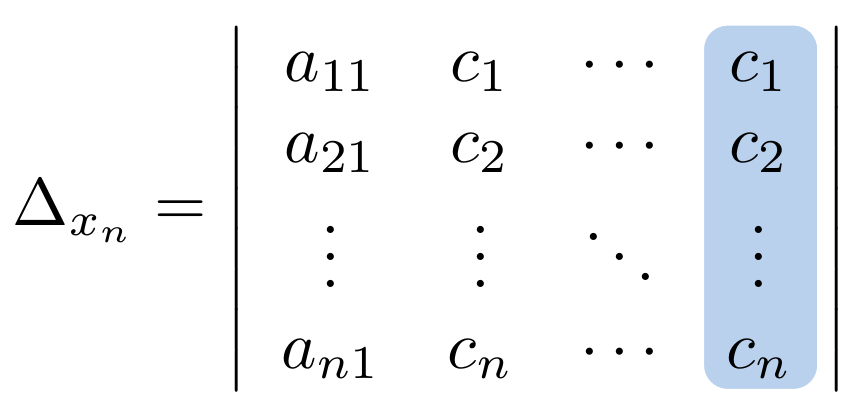
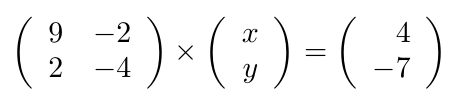
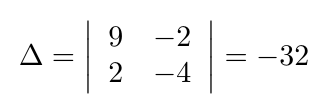
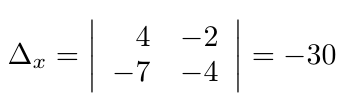
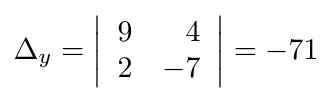
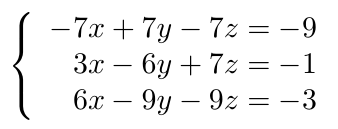

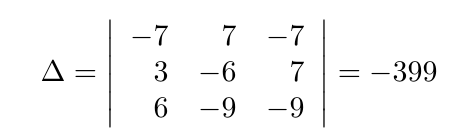
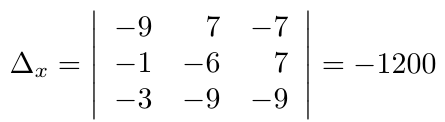
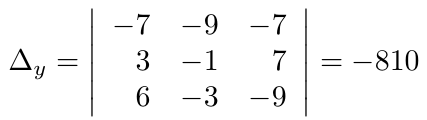
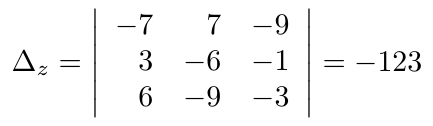

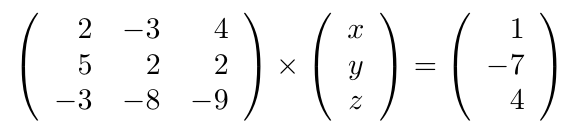
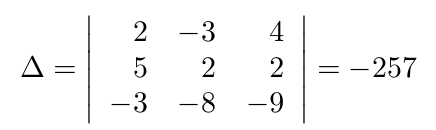
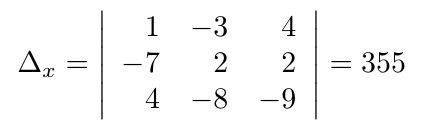
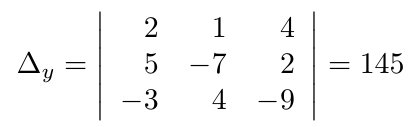
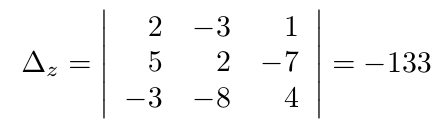
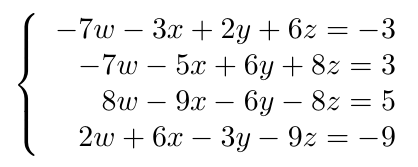
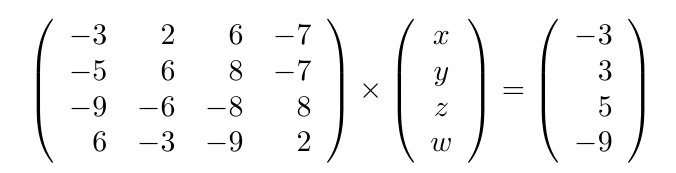
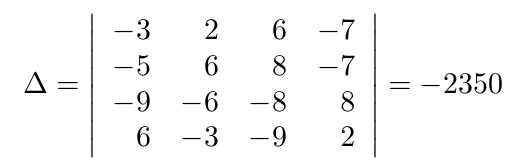
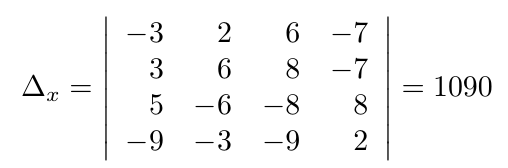
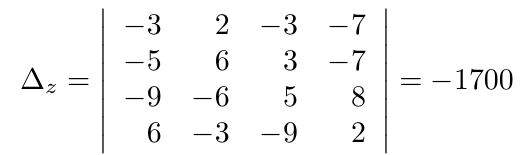
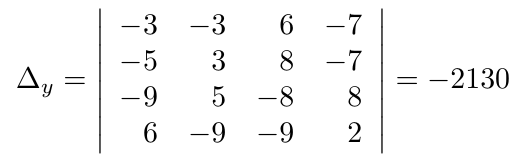
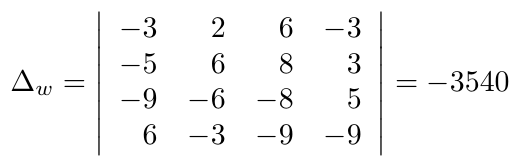



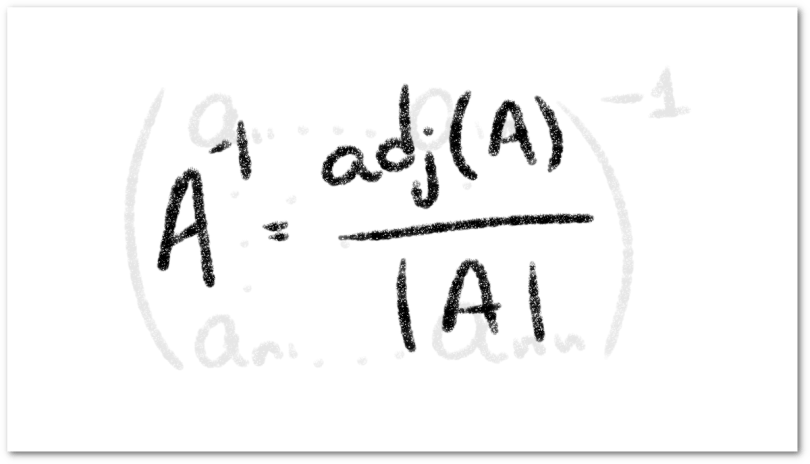


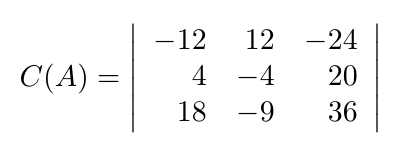
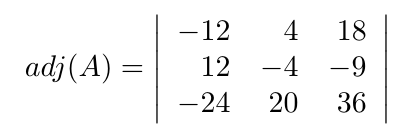
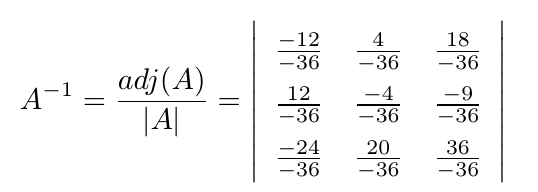
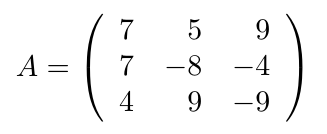
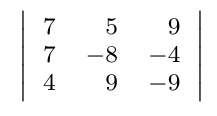
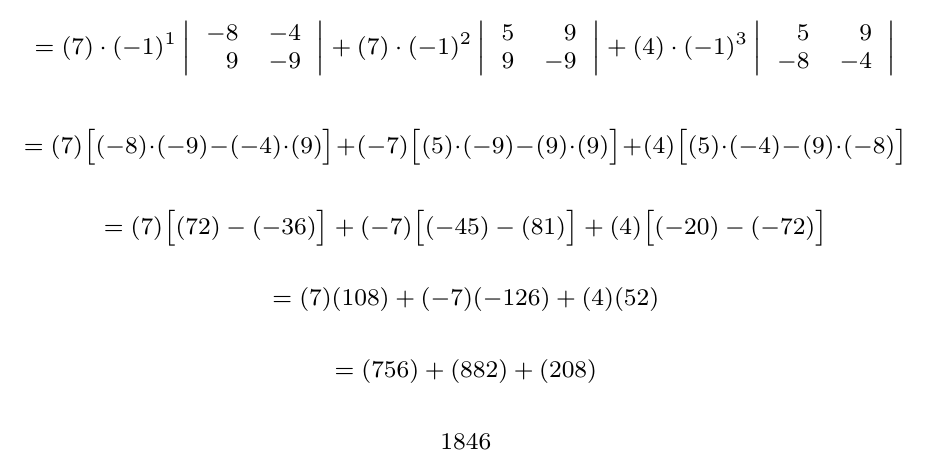
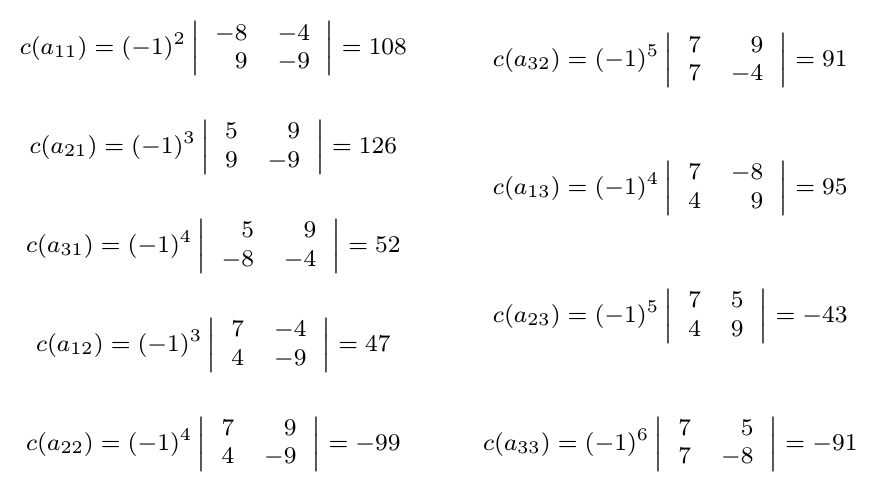
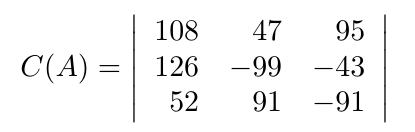
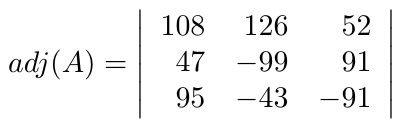
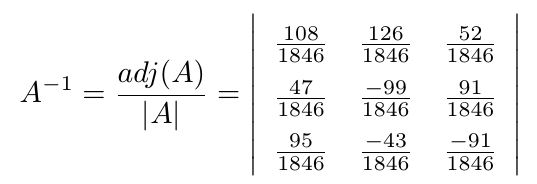
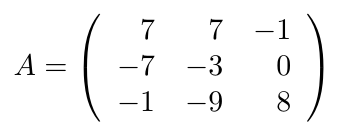
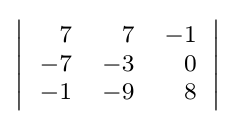
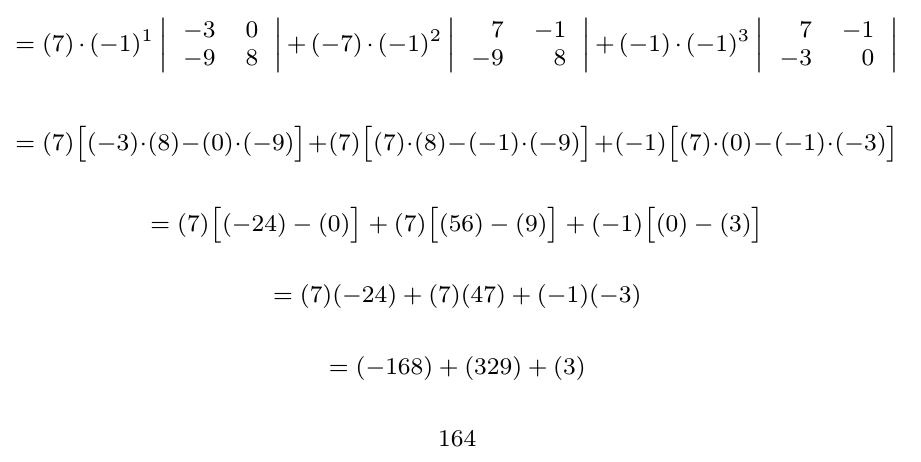

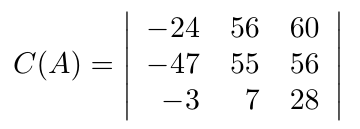


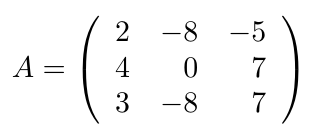
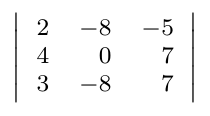
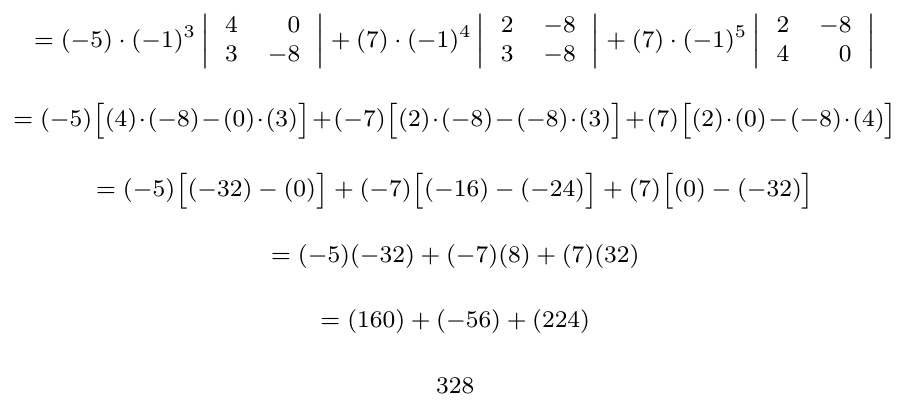

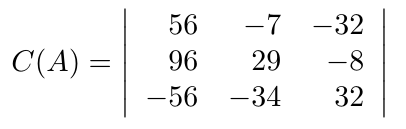
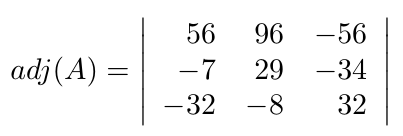
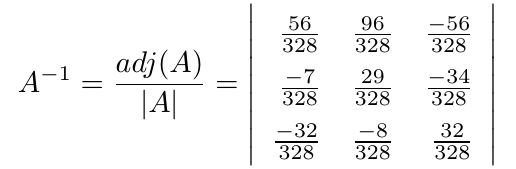
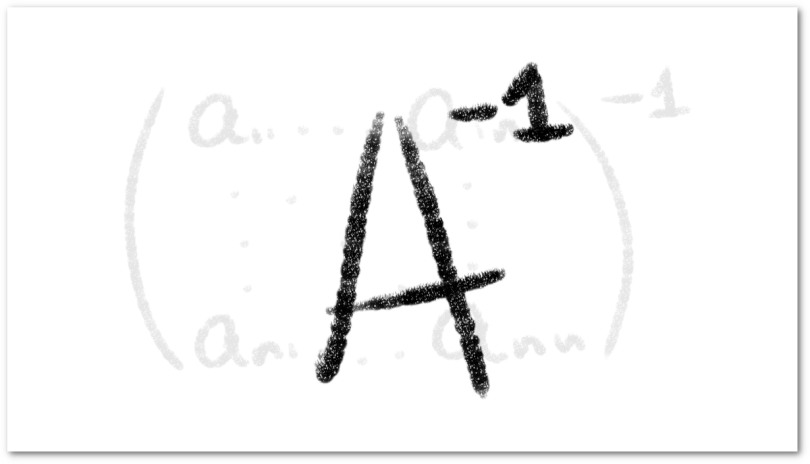
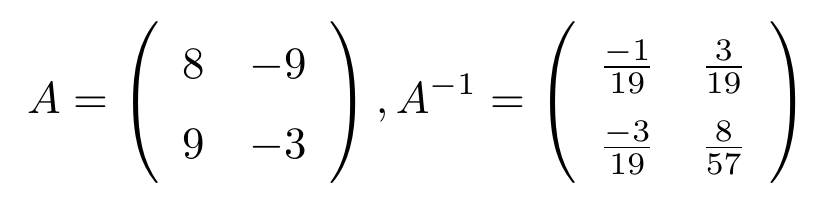
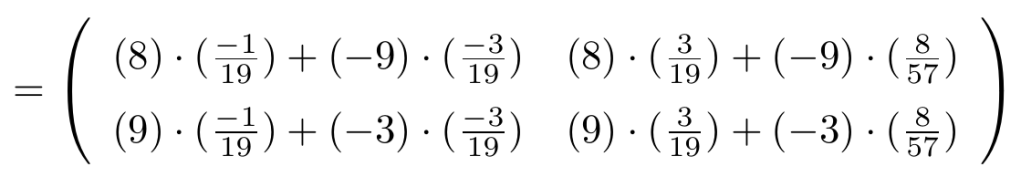
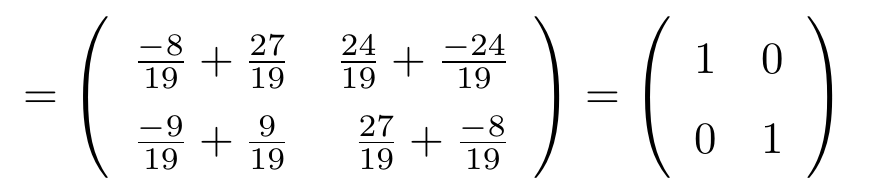
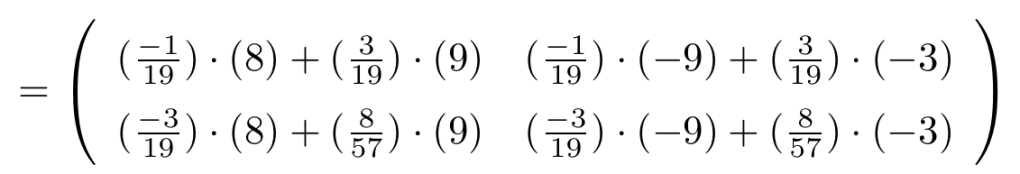
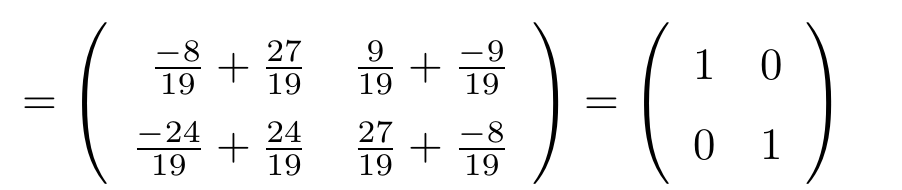
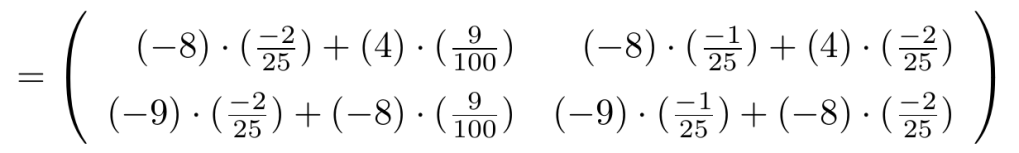

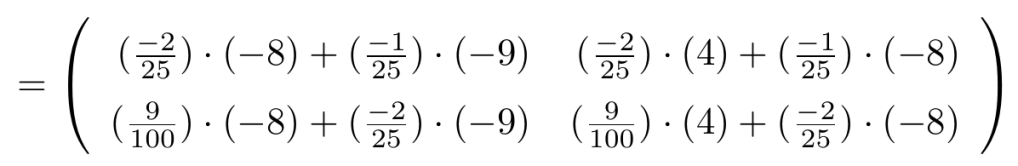
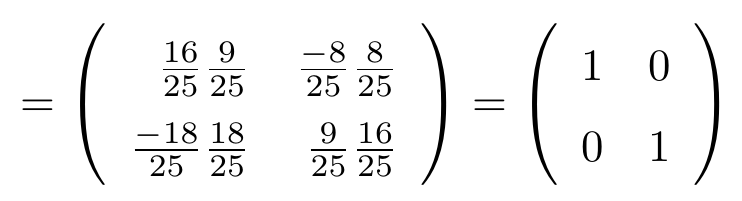
Debe estar conectado para enviar un comentario.