En ocasiones, es necesario cambiar las filas por columnas de una matriz y viceversa, para esto definimos la operación de transposición. Sea 
una matriz de tamaño 
decimos que la transposición de la matriz es una nueva matriz de tamaño 
donde los elementos de la matriz que están en la posición 
pasan a estar en la posición 
, a esta nueva matriz se le llama transpuesta (o traspuesta) y la denotamos por 
o 
. Formalmente,
![[A^{T}]_{ij} = A_{ji}](https://s0.wp.com/latex.php?latex=%5BA%5E%7BT%7D%5D_%7Bij%7D+%3D+A_%7Bji%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
O escrito de forma exhaustiva, tenemos que
Veamos algunos ejemplos.
Ejemplos
Ejemplos 17
Considerando la matriz A, de tamaño, 
. Calcule la matriz transpuesta de A, es decir, .
Ejemplos 18
Considerando la matriz A, de tamaño, 
. Calcule la matriz transpuesta de A, es decir, .
Ejemplo 19
Considerando la matriz A, de tamaño, 
. Calcule la matriz transpuesta de A, es decir, .
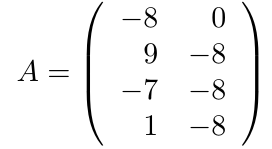
Ejemplo 20
Considerando la matriz A, de tamaño, 
. Calcule la matriz transpuesta de A, es decir, .
totumat 
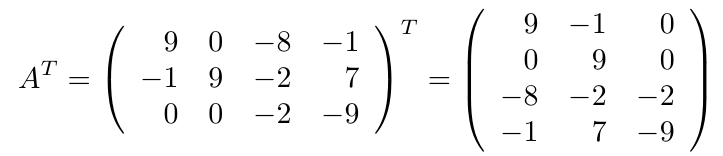
Un saludo
Me refiero, ¿cuál es su aplicación en un caso práctico? En un conjunto de ecuaciones por resolver ¿es necesario aplicar esta operación?
Me gustaMe gusta
Efectivamente, la transposición de matrices tiene distintas aplicaciones, principalmente en el desarrollo teórico del álgebra lineal, por ejemplo, para calcular la inversa de una matriz, es necesario calcular matriz de cofactores y posteriormente esta se debe transponer para poder calcular la matriz adjunta.
También en el desarrollo teórico de modelos estadísticos, por ejemplo, para definir modelos de regresión lineal, los parámetros óptimos se definen con un producto de matrices en los que es necesario transponer algunas de las matrices involucradas para poder efectuar el producto (recordemos que el número de columnas del primer factor debe coincidir con el número de filas del segundo factor).
Me gustaMe gusta