Sobre el conjunto de las matrices podemos definir operaciones de suma, resta, multiplicación por un escalar y multiplicación entre dos matrices. Además, definiremos una operación que se aplica sobre una sola matriz que llamaremos transposición.
También pudiera interesarte
Suma de Matrices
Sean y
dos matrices de tamaño
, definimos la suma
como una nueva matriz donde cada elemento
de esta nueva matriz, está definido como la suma del elemento
de la matriz
más el elemento
de la matriz
. Formalmente,
O escrito de forma exhaustiva, tenemos que

Veamos algunos ejemplos.
Ejemplos
Ejemplo 1
Considerando las matrices A y B, de tamaño , calcule la suma indicada.


Ejemplo 2
Considerando las matrices A y B, de tamaño , calcule la suma indicada.


Ejemplo 3
Considerando las matrices A y B, de tamaño, calcule la suma indicada.


Ejemplo 4
Considerando las matrices A y B, de tamaño, calcule la suma indicada.


Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Resta de Matrices
Sean y
dos matrices de tamaño
, definimos la resta
como una nueva matriz donde cada elemento
de esta nueva matriz, está definido como la resta del elemento
de la matriz
menos el elemento
de la matriz
. Formalmente,
O escrito de forma exhaustiva, tenemos que

Debemos tomar en cuenta que al restar la matriz , cada uno de los elementos de esta matriz es multiplicado por
. Veamos algunos ejemplos.
Ejemplos
Ejemplo 5
Considerando las matrices A y B, de tamaño, calcule la suma indicada.
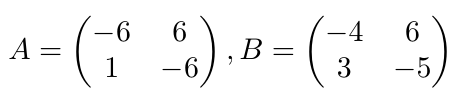

Ejemplo 6
Considerando las matrices A y B, de tamaño, calcule la suma indicada.


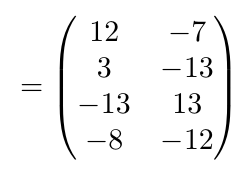
Ejemplo 7
Considerando las matrices A y B, de tamaño, calcule la suma indicada.



Ejemplo 8
Considerando las matrices A y B, de tamaño, calcule la suma indicada.


Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Multiplicación por un escalar
Diremos que un escalar es un número real que al multiplicarla por una matriz esta nos cambia la escala de cada uno de los elementos de ella. Definimos el producto de un escalar por una matriz
, como una nueva matriz donde cada elemento
de esta nueva matriz, está definido como el producto del escalar
por el elemento
de la matriz
. Formalmente,
O escrito de forma exhaustiva, tenemos que

Veamos algunos ejemplos.
Ejemplos
Ejemplo 9
Considerando la matriz A, de tamaño, calcule el producto por el escalar
.

Ejemplo 10
Considerando la matriz A, de tamaño, calcule el producto por el escalar
.

Ejemplo 11
Considerando la matriz A, de tamaño, calcule el producto por el escalar
.

Ejemplo 12
Considerando la matriz A, de tamaño, calcule el producto por el escalar
.
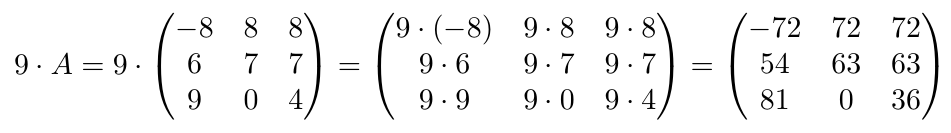
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Producto entre Matrices
Sean una matriz de tamaño
y
una matriz de tamaño
, definimos el producto
como una nueva matriz donde cada elemento
de esta nueva matriz, está definido el «producto» de la fila
de la matriz
por la columna
de la matriz
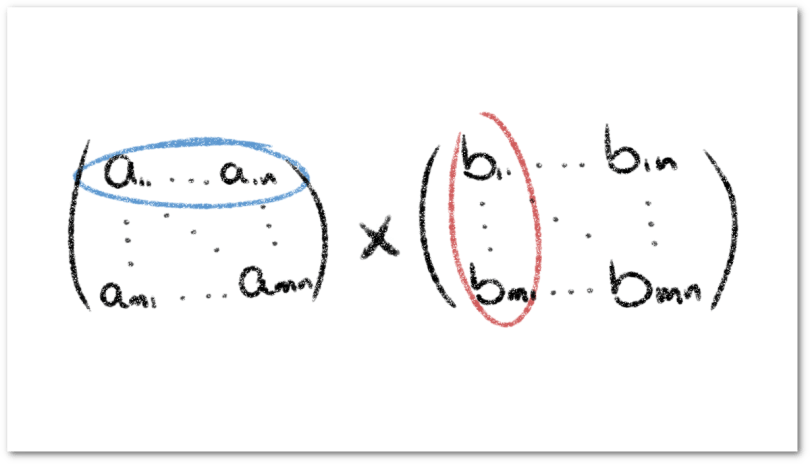
. Formalmente,
Debemos notar que para poder efectuar esta operación, el número de columnas de la matriz debe ser exactamente igual al número de filas de la matriz
y aunque esta operación pareciera complicada, en los siguientes ejemplos veremos el procedimiento para calcular el producto entre dos matrices.
Ejemplos
Ejemplo 13
Considerando la matriz A, de tamaño, y la matriz B, de tamaño,
. Calcule el producto
. Veamos en este ejemplo paso a paso como calcular este producto.

El elemento de la nueva matriz
es el resultado de multiplicar la fila
por la columna
.

El elemento de la nueva matriz
es el resultado de multiplicar la fila
por la columna
.
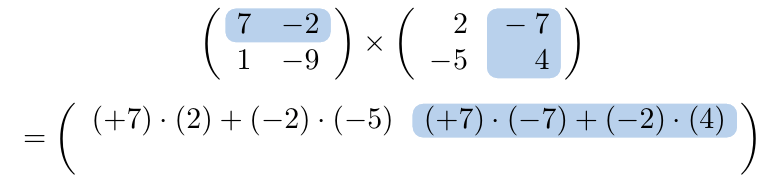
El elemento de la nueva matriz
es el resultado de multiplicar la fila
por la columna
.

El elemento de la nueva matriz
es el resultado de multiplicar la fila
por la columna
.

De esta forma, tenemos que

Entonces, aplicamos las operaciones involucradas

Ejemplo 14
Considerando la matriz , de tamaño,
y la matriz
, de tamaño,
. Calcule el producto
.




Ejemplo 15
Considerando la matriz , de tamaño,
y la matriz
, de tamaño,
. Calcule el producto
.

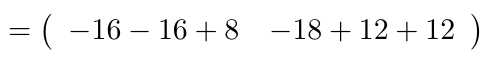

Ejemplo 16
Considerando la matriz , de tamaño,
y la matriz
, de tamaño,
. Calcule el producto
.



Nota: Si podemos multiplicar , no necesariamente podemos multiplicar
, esto quiere decir que el producto entre matrices no es conmutativo.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Transposición de matrices
En ocasiones, es necesario cambiar las filas por columnas de una matriz y viceversa, para esto definimos la operación de transposición. Sea una matriz de tamaño
decimos que la transposición de la matriz
es una nueva matriz de tamaño
donde los elementos de la matriz
que están en la posición
pasan a estar en la posición
, a esta nueva matriz se le llama
traspuesta (o traspuesta) y la denotamos por
o
. Formalmente,
O escrito de forma exhaustiva, tenemos que

Veamos algunos ejemplos.
Ejemplos
Ejemplos 17
Considerando la matriz A, de tamaño, . Calcule la matriz transpuesta de A, es decir,
.


Ejemplos 18
Considerando la matriz A, de tamaño, . Calcule la matriz transpuesta de A, es decir,
.


Ejemplo 19
Considerando la matriz A, de tamaño, . Calcule la matriz transpuesta de A, es decir,
.
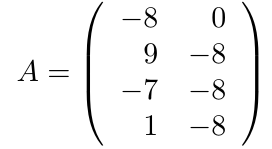

Ejemplo 20
Considerando la matriz A, de tamaño, . Calcule la matriz transpuesta de A, es decir,
.

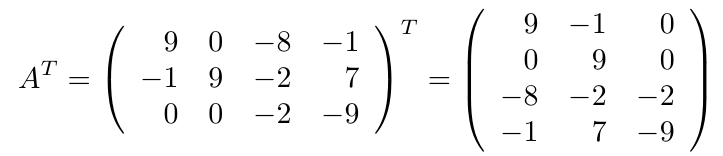














Debe estar conectado para enviar un comentario.