- Determinante del Producto de Matrices
- Ejemplos
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
- Ejemplo 4
- Determinante de la matriz transpuesta
- Ejemplos
- Ejemplo 5
- Ejemplo 6
- Ejemplo 7
- Ejemplo 8
- Determinante de descomponer elementos como sumandos
- Ejemplos
- Ejemplo 9
- Ejemplo 10
- Ejemplo 11
- Ejemplo 12
- Determinante de multiplicar un escalar por una fila o columna
- Ejemplos
- Ejemplo 13
- Ejemplo 14
- Ejemplo 15
- Ejemplo 16
- Determinante de multiplicar un escalar por una matriz
- Ejemplos
- Ejemplo 17
- Ejemplo 18
- Determinante de una matriz con fila o columna cero
- Ejemplos
- Ejemplo 19
- Ejemplo 20
- Ejemplo 21
- Ejemplo 22
- Determinante de una matriz con filas o columnas iguales
- Ejemplos
- Ejemplo 23
- Ejemplo 24
- Ejemplo 25
- Determinante de una matriz con fila o columna proporcional a otra
- Ejemplos
- Ejemplo 26
- Ejemplo 27
- Ejemplo 28
- Ejemplo 29
- Determinante de una matriz con filas o columnas linealmente dependientes
- Ejemplos
- Ejemplo 30
- Ejemplo 31
- Ejemplo 32
- Ejemplo 33
- Determinante de una matriz con intercambio de filas o columnas
- Ejemplos
- Ejemplo 34
- Ejemplo 35
- Ejemplo 36
- Ejemplo 37
- Determinante de una matriz con filas o columnas sumadas
- Ejemplos
- Ejemplo 38
- Ejemplo 39
- Ejemplo 40
- Ejemplo 41
- Determinante de una matriz con suma de filas o columnas multiplicadas por un escalar
- Ejemplos
- Ejemplo 42
- Ejemplo 43
- Ejemplo 44
- Ejemplo 45
- Determinante de la Matriz Inversa
Calcular determinantes, ya sea por el Método de Laplace o por el Método de Sarrus puede resultar en un proceso extenso, es por esto que estudiaremos con detenimiento cómo la forma en la que está definida una matriz, nos puede ahorrar tiempo a la hora de calcular el determinante.
También pudiera interesarte
En esta sección están expuestas las siguientes propiedades con sus respectivos ejemplos:
Determinante del Producto de Matrices
Si consideramos dos matrices cuadradas  y
y 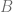 , el determinante del producto entre estas dos matrices
, el determinante del producto entre estas dos matrices 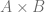 es exactamente igual al determinante de la matriz
es exactamente igual al determinante de la matriz  multiplicado por el determinante de la matriz
multiplicado por el determinante de la matriz 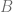 , es decir,
, es decir,

Veamos algunos ejemplos de este tipo de determinantes,
Ejemplos
Ejemplo 1
Considerando las matrices cuadrada  y
y 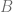 de tamaño dos calculemos el determinante de cada una de ellas,
de tamaño dos calculemos el determinante de cada una de ellas,
El producto de estos dos determinantes es igual a -588, veamos que este producto es igual al determinante del producto de las dos matrices.
Ejemplo 2
Considerando las matrices cuadrada  y
y 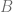 de tamaño dos calculemos el determinante de cada una de ellas,
de tamaño dos calculemos el determinante de cada una de ellas,
El producto de estos dos determinantes es igual a -405, veamos que este producto es igual al determinante del producto de las dos matrices.
Ejemplo 3
Considerando las matrices cuadrada  y
y 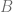 de tamaño dos, calculemos el determinante de cada una de ellas,
de tamaño dos, calculemos el determinante de cada una de ellas,
El producto de estos dos determinantes es igual a 2064, veamos que este producto es igual al determinante del producto de las dos matrices.
Ejemplo 4
Considerando las matrices cuadrada  y
y 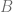 de tamaño dos, calculemos el determinante de cada una de ellas,
de tamaño dos, calculemos el determinante de cada una de ellas,
El producto de estos dos determinantes es igual a -4851, veamos que este producto es igual al determinante del producto de las dos matrices.
Determinante de la matriz transpuesta
Si consideramos una matriz cuadrada  , el determinante de la matriz transpuesta
, el determinante de la matriz transpuesta  es exactamente igual al determinante de la matriz
es exactamente igual al determinante de la matriz  , es decir,
, es decir,  .
.
Veamos algunos ejemplos de este tipo de determinantes,
Ejemplos
Ejemplo 5
Considerando la matriz cuadrada  de tamaño dos, podemos calcular el determinante de esta matriz y su transpuesta para notar que
de tamaño dos, podemos calcular el determinante de esta matriz y su transpuesta para notar que 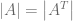 .
.
Ejemplo 6
Considerando la matriz cuadrada  de tamaño dos, podemos calcular el determinante de esta matriz y su transpuesta para notar que
de tamaño dos, podemos calcular el determinante de esta matriz y su transpuesta para notar que 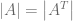 .
.
Ejemplo 7
Considerando la matriz cuadrada  de tamaño tres, podemos calcular el determinante de esta matriz y su transpuesta para notar que
de tamaño tres, podemos calcular el determinante de esta matriz y su transpuesta para notar que 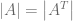 .
.
Ejemplo 8
Considerando la matriz cuadrada  de tamaño tres, podemos calcular el determinante de esta matriz y su transpuesta para notar que
de tamaño tres, podemos calcular el determinante de esta matriz y su transpuesta para notar que 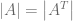 .
.
Determinante de descomponer elementos como sumandos
Si consideramos una matriz y descomponemos todos los elementos de una fila en dos sumandos, el determinante de la matriz se puede descomponer como la suma de dos determinantes donde la primera matriz contiene sólo los primeros sumandos y la otra matriz contiene sólo los segundos sumandos.
Formalmente, si consideramos una matriz  donde cada elemento elemento
donde cada elemento elemento  de la fila
de la fila 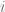 se puede descomponer como
se puede descomponer como  , entonces tenemos que
, entonces tenemos que
Por otra parte, si consideramos una matriz  donde cada elemento elemento
donde cada elemento elemento  de la columna
de la columna 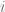 se puede descomponer como
se puede descomponer como  , entonces tenemos que
, entonces tenemos que
Veamos algunos ejemplos de este tipo de determinantes.
Ejemplos
Ejemplo 9
Considerando la matriz cuadrada  de tamaño dos, descompongamos los elementos de la fila
de tamaño dos, descompongamos los elementos de la fila 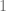 .
.
Descomponemos los elementos de la fila 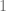 en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de
en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de 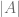 .
.
Ejemplo 10
Considerando la matriz cuadrada  de tamaño dos, descompongamos los elementos de la columna
de tamaño dos, descompongamos los elementos de la columna 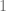 .
.
Descomponemos los elementos de la columna 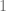 en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de
en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de 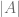 .
.
Ejemplo 11
Considerando la matriz cuadrada  de tamaño dos, descompongamos los elementos de la fila
de tamaño dos, descompongamos los elementos de la fila 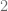 .
.
Descomponemos los elementos de la fila 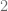 en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de
en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de 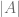 .
.
Ejemplo 12
Considerando la matriz cuadrada  de tamaño dos, descompongamos los elementos de la columna
de tamaño dos, descompongamos los elementos de la columna 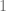 .
.
Descomponemos los elementos de la columna 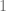 en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de
en dos sumandos y calculamos los determinantes respectivos para verificar que la suma de estos es igual al determinante de 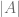 .
.
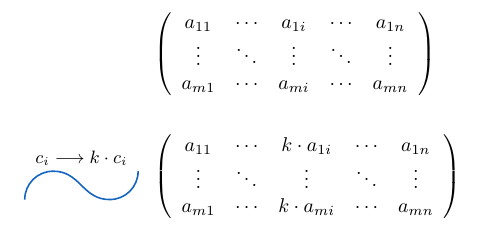
Determinante de multiplicar un escalar por una fila o columna
Si consideramos una matriz  , el determinante de la matriz que resulta al multiplicar una fila o una columna por un escalar
, el determinante de la matriz que resulta al multiplicar una fila o una columna por un escalar 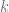 es exactamente igual al determinante de la matriz
es exactamente igual al determinante de la matriz  multiplicada por el escalar
multiplicada por el escalar 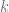 , es decir,
, es decir, 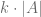
ó
Veamos algunos ejemplos de este tipo de determinantes,
Ejemplos
Ejemplo 13
Considerando la matriz cuadrada  de tamaño dos, podemos notar que al multiplicar una fila por el escalar
de tamaño dos, podemos notar que al multiplicar una fila por el escalar  , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a  .
.
Multiplicamos la fila 1 por la el escalar 9 y calculamos el determinante de la matriz resultante.
Ejemplo 14
Considerando la matriz cuadrada  de tamaño dos, podemos notar que al multiplicar una fila por el escalar
de tamaño dos, podemos notar que al multiplicar una fila por el escalar  , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a  .
.
Multiplicamos la fila 2 por la el escalar 5 y calculamos el determinante de la matriz resultante.
Ejemplo 15
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al multiplicar una fila por el escalar
de tamaño tres, podemos notar que al multiplicar una fila por el escalar 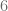 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a  .
.
Multiplicamos la fila 2 por la el escalar 6 y calculamos el determinante de la matriz resultante.
Ejemplo 16
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al multiplicar una fila por el escalar
de tamaño tres, podemos notar que al multiplicar una fila por el escalar  , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a  .
.
Multiplicamos la columna 1 por la el escalar 4 y calculamos el determinante de la matriz resultante.
Determinante de multiplicar un escalar por una matriz
Si consideramos una matriz  cuadrada de tamaño
cuadrada de tamaño  , el determinante de la matriz que resulta al multiplicar esta matriz por un escalar
, el determinante de la matriz que resulta al multiplicar esta matriz por un escalar 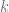 es exactamente igual al determinante de la matriz
es exactamente igual al determinante de la matriz  multiplicada por el escalar
multiplicada por el escalar 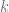 elevado a la
elevado a la  , es decir,
, es decir, 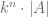
Veamos algunos ejemplos de este tipo de determinantes,
Ejemplos
Ejemplo 17
Considerando la matriz cuadrada  de tamaño dos, podemos notar que al multiplicar esta matriz por el escalar
de tamaño dos, podemos notar que al multiplicar esta matriz por el escalar 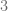 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 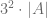 .
.
Multiplicamos la matriz  por la el escalar 3 y calculamos el determinante de la matriz resultante.
por la el escalar 3 y calculamos el determinante de la matriz resultante.
Ejemplo 18
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al multiplicar esta matriz por el escalar
de tamaño tres, podemos notar que al multiplicar esta matriz por el escalar 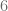 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 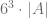 .
.
Multiplicamos la matriz  por la el escalar 6 y calculamos el determinante de la matriz resultante.
por la el escalar 6 y calculamos el determinante de la matriz resultante.
Determinante de una matriz con fila o columna cero
Si consideramos una matriz  tal que al menos una de sus filas o una de sus columnas está compuesta de ceros, el determinante esta matriz es igual a cero.
tal que al menos una de sus filas o una de sus columnas está compuesta de ceros, el determinante esta matriz es igual a cero.
Veamos algunos ejemplos de este tipo de determinantes.
Ejemplos
Ejemplo 19
Considerando la matriz cuadrada  de tamaño dos, podemos notar que si una de sus filas es igual a cero, el determinante de la matriz resultante es igual a cero.
de tamaño dos, podemos notar que si una de sus filas es igual a cero, el determinante de la matriz resultante es igual a cero.
Ejemplo 20
Considerando la matriz cuadrada  de tamaño dos, podemos notar que si una de sus columnas es igual a cero, el determinante de la matriz resultante es igual a cero.
de tamaño dos, podemos notar que si una de sus columnas es igual a cero, el determinante de la matriz resultante es igual a cero.
Ejemplo 21
Considerando la matriz cuadrada  de tamaño tres, podemos notar que si una de sus filas es igual a cero, el determinante de la matriz resultante es igual a cero.
de tamaño tres, podemos notar que si una de sus filas es igual a cero, el determinante de la matriz resultante es igual a cero.
Ejemplo 22
Considerando la matriz cuadrada  de tamaño tres, podemos notar que si una de sus columnas es igual a cero, el determinante de la matriz resultante es igual a cero.
de tamaño tres, podemos notar que si una de sus columnas es igual a cero, el determinante de la matriz resultante es igual a cero.
Determinante de una matriz con filas o columnas iguales
Si consideramos una matriz  tal que al menos dos de sus filas o al menos dos de sus columnas son iguales, el determinante esta matriz es igual a cero. Veamos algunos ejemplos de este tipo de determinantes.
tal que al menos dos de sus filas o al menos dos de sus columnas son iguales, el determinante esta matriz es igual a cero. Veamos algunos ejemplos de este tipo de determinantes.
ó
Ejemplos
Ejemplo 23
Considerando la matriz cuadrada  de tamaño dos, podemos notar que si una de sus filas o sus columnas es igual a otra, el determinante de la matriz resultante es igual a cero.
de tamaño dos, podemos notar que si una de sus filas o sus columnas es igual a otra, el determinante de la matriz resultante es igual a cero.
Ejemplo 24
Considerando la matriz cuadrada  de tamaño dos, podemos notar que si una de sus filas es igual a otra, el determinante de la matriz resultante es igual a cero.
de tamaño dos, podemos notar que si una de sus filas es igual a otra, el determinante de la matriz resultante es igual a cero.
Ejemplo 25
Considerando la matriz cuadrada  de tamaño tres, podemos notar que si una de sus columnas es igual a otra, el determinante de la matriz resultante es igual a cero.
de tamaño tres, podemos notar que si una de sus columnas es igual a otra, el determinante de la matriz resultante es igual a cero.
Determinante de una matriz con fila o columna proporcional a otra
Si consideramos una matriz  tal que al menos una de sus filas o al menos una de sus columnas es proporcional a otra, es decir, que está expresada como un múltiplo de otra, el determinante esta matriz es igual a cero.
tal que al menos una de sus filas o al menos una de sus columnas es proporcional a otra, es decir, que está expresada como un múltiplo de otra, el determinante esta matriz es igual a cero.
ó
Veamos algunos ejemplos de este tipo de determinantes.
Ejemplos
Ejemplo 26
Considerando la matriz cuadrada  de tamaño dos, podemos notar que si una de sus filas es proporcional otra, el determinante de la matriz resultante es igual a cero.
de tamaño dos, podemos notar que si una de sus filas es proporcional otra, el determinante de la matriz resultante es igual a cero.
Ejemplo 27
Considerando la matriz cuadrada  de tamaño dos, podemos notar que si una de sus columnas es proporcional otra, el determinante de la matriz resultante es igual a cero.
de tamaño dos, podemos notar que si una de sus columnas es proporcional otra, el determinante de la matriz resultante es igual a cero.
Ejemplo 28
Considerando la matriz cuadrada  de tamaño tres, podemos notar que si una de sus filas es proporcional a otra, el determinante de la matriz resultante es igual a cero.
de tamaño tres, podemos notar que si una de sus filas es proporcional a otra, el determinante de la matriz resultante es igual a cero.
Ejemplo 29
Considerando la matriz cuadrada  de tamaño tres, podemos notar que si una de sus columnas es proporcional a otra, el determinante de la matriz resultante es igual a cero.
de tamaño tres, podemos notar que si una de sus columnas es proporcional a otra, el determinante de la matriz resultante es igual a cero.
Determinante de una matriz con filas o columnas linealmente dependientes
Si consideramos una matriz  tal que el conjunto de sus filas o el conjunto de sus columnas es linealmente dependiente, es decir, tal que al menos una de sus filas o al menos de sus columnas está expresada como combinación lineal de las otras, el determinante esta matriz es igual a cero.
tal que el conjunto de sus filas o el conjunto de sus columnas es linealmente dependiente, es decir, tal que al menos una de sus filas o al menos de sus columnas está expresada como combinación lineal de las otras, el determinante esta matriz es igual a cero.
También podemos afirmar que si las filas o las columnas de una matriz son linealmente independientes, entonces su determinante es distinto de cero.
Veamos algunos ejemplos de este tipo de determinantes.
Ejemplos
Ejemplo 30
Considerando la matriz cuadrada  de tamaño tres, podemos notar que la fila
de tamaño tres, podemos notar que la fila 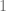 está expresada como combinación lineal de las otras filas, el determinante de la matriz resultante es igual a cero.
está expresada como combinación lineal de las otras filas, el determinante de la matriz resultante es igual a cero.
Ejemplo 31
Considerando la matriz cuadrada  de tamaño tres, podemos notar que la fila
de tamaño tres, podemos notar que la fila 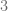 está expresada como combinación lineal de las otras filas, el determinante de la matriz resultante es igual a cero.
está expresada como combinación lineal de las otras filas, el determinante de la matriz resultante es igual a cero.
Ejemplo 32
Considerando la matriz cuadrada  de tamaño tres, podemos notar que la columna
de tamaño tres, podemos notar que la columna 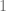 está expresada como combinación lineal de las otras columnas, el determinante de la matriz resultante es igual a cero.
está expresada como combinación lineal de las otras columnas, el determinante de la matriz resultante es igual a cero.
Ejemplo 33
Considerando la matriz cuadrada  de tamaño tres, podemos notar que la columna
de tamaño tres, podemos notar que la columna 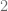 está expresada como combinación lineal de las otras columnas, el determinante de la matriz resultante es igual a cero.
está expresada como combinación lineal de las otras columnas, el determinante de la matriz resultante es igual a cero.
Determinante de una matriz con intercambio de filas o columnas
Si consideramos una matriz  , el determinante de la matriz que resulta de intercambiar dos filas o columnas es exactamente igual al determinante de la matriz
, el determinante de la matriz que resulta de intercambiar dos filas o columnas es exactamente igual al determinante de la matriz  pero con signo contrario, es decir, igual a
pero con signo contrario, es decir, igual a  .
.
Formalmente, si intercambiamos la fila 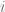 por la
por la 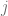 , tenemos que
, tenemos que
Por otra parte, si intercambiamos la columna 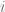 por la
por la 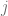 , tenemos que
, tenemos que
Veamos algunos ejemplos de este tipo de determinantes,
Ejemplos
Ejemplo 34
Considerando la matriz cuadrada  de tamaño dos, podemos notar que al intercambiar dos filas, el determinante de la matriz resultante es igual a
de tamaño dos, podemos notar que al intercambiar dos filas, el determinante de la matriz resultante es igual a  .
.
Intercambiamos la fila 1 por la fila 2 y calculamos el determinante de la matriz resultante.
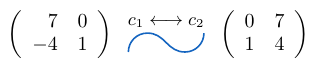
Ejemplo 35
Considerando la matriz cuadrada  de tamaño dos, podemos notar que al intercambiar dos columnas, el determinante de la matriz resultante es igual a
de tamaño dos, podemos notar que al intercambiar dos columnas, el determinante de la matriz resultante es igual a  .
.
Intercambiamos la columna 1 por la columna 2 y calculamos el determinante de la matriz resultante.
Ejemplo 36
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al intercambiar dos filas, el determinante de la matriz resultante es igual a
de tamaño tres, podemos notar que al intercambiar dos filas, el determinante de la matriz resultante es igual a  .
.
Intercambiamos la fila 1 por la fila 2 y calculamos el determinante de la matriz resultante.
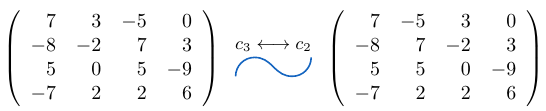
Ejemplo 37
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al intercambiar dos columnas, el determinante de la matriz resultante es igual a
de tamaño tres, podemos notar que al intercambiar dos columnas, el determinante de la matriz resultante es igual a  .
.
Intercambiamos la columna 1 por la columna 3 y calculamos el determinante de la matriz resultante.
Determinante de una matriz con filas o columnas sumadas
Si consideramos una matriz  , el determinante de la matriz que resulta de sumar dos filas o columnas es exactamente igual al determinante de la matriz
, el determinante de la matriz que resulta de sumar dos filas o columnas es exactamente igual al determinante de la matriz  .
.
ó
Veamos algunos ejemplos de este tipo de determinantes.
Ejemplos
Ejemplo 38
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la fila
de tamaño tres, podemos notar que al sumar la fila 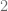 a la fila
a la fila 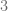 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 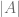 .
.
Sumamos la fila 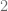 a la fila
a la fila 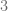 .
.
Ejemplo 39
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la fila
de tamaño tres, podemos notar que al sumar la fila 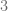 a la fila
a la fila 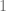 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 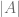 .
.
Sumamos la fila 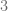 a la fila
a la fila 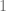 .
.
Ejemplo 40
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la columna
de tamaño tres, podemos notar que al sumar la columna 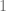 a la columna
a la columna 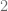 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 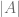 .
.
Sumamos la columna 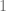 a la columna
a la columna 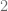 .
.
Ejemplo 41
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la columna
de tamaño tres, podemos notar que al sumar la columna 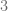 a la columna
a la columna 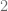 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 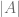 .
.
Sumamos la columna 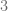 a la columna
a la columna 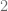 .
.
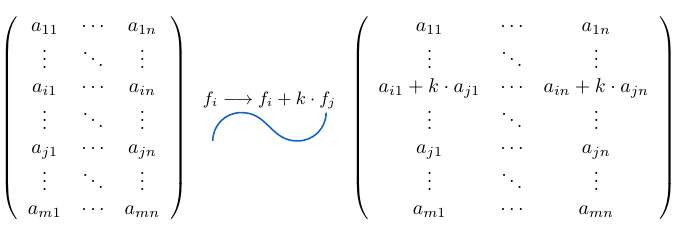
Determinante de una matriz con suma de filas o columnas multiplicadas por un escalar
Si consideramos una matriz  , el determinante de la matriz que resulta de sumar a una fila otra fila multiplicada por un escalar o de sumar a columna otra columna multiplicada por un escalar, es exactamente igual al determinante de la matriz
, el determinante de la matriz que resulta de sumar a una fila otra fila multiplicada por un escalar o de sumar a columna otra columna multiplicada por un escalar, es exactamente igual al determinante de la matriz  .
.
ó
Veamos algunos ejemplos de este tipo de determinantes.
Ejemplos
Ejemplo 42
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la fila
de tamaño tres, podemos notar que al sumar la fila 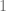 a la fila
a la fila 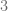 multiplicada por
multiplicada por  , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 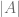 .
.
Sumamos la fila 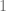 a la fila
a la fila 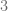 multiplicada por
multiplicada por  .
.
Ejemplo 43
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la fila
de tamaño tres, podemos notar que al sumar la fila 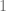 a la fila
a la fila 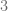 multiplicada por
multiplicada por 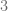 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 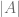 .
.
Sumamos la fila 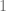 a la fila
a la fila 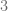 multiplicada por
multiplicada por 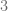 .
.
Ejemplo 44
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la columna
de tamaño tres, podemos notar que al sumar la columna 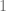 a la columna
a la columna 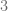 multiplicada por
multiplicada por 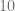 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 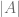 .
.
Sumamos la columna 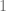 a la columna
a la columna 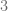 multiplicada por
multiplicada por 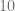 .
.
Ejemplo 45
Considerando la matriz cuadrada  de tamaño tres, podemos notar que al sumar la columna
de tamaño tres, podemos notar que al sumar la columna 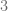 a la columna
a la columna 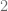 multiplicada por
multiplicada por 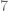 , el determinante de la matriz resultante es igual a
, el determinante de la matriz resultante es igual a 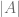 .
.
Sumamos la columna 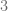 a la columna
a la columna 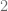 multiplicada por
multiplicada por 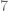 .
.
Determinante de la Matriz Inversa
Si consideramos  una matriz no-singular, definimos la matriz inversa de
una matriz no-singular, definimos la matriz inversa de  como una nueva matriz
como una nueva matriz  que cumple con la siguiente condición:
que cumple con la siguiente condición:
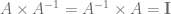
El determinante de la matriz inversa de  se puede deducir fácilmente de las otras propiedades y es exactamente igual al inverso multiplicativo del determinante de
se puede deducir fácilmente de las otras propiedades y es exactamente igual al inverso multiplicativo del determinante de  , es decir,
, es decir,
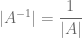
Esto se debe a
ecuaciones y
incógnitas de forma matricial, es decir, de la siguiente forma:

es una matriz cuadrada no-singular, es decir, tal que su determinante es distinto de cero. Podemos usar el Método de Eliminación de Gauss-Jordan para calcular la solución del sistema de ecuaciones ampliando la matriz
adosando la matriz de términos independientes
a su lado derecho, de la siguiente forma:
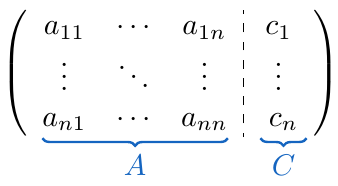
ecuaciones y
incógnitas. Calcule la solución del mismo usando el Método de Eliminación de Gauss-Jordan.
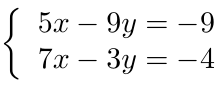
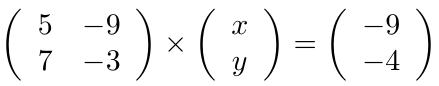
para verificar que éste sea diferente de cero,
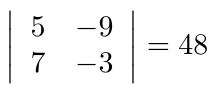
es distinto de cero, ampliamos la matriz adosando la matriz $C$ en el lado derecho y aplicamos el Método de Eliminación de Gauss-Jordan sobre la matriz
.
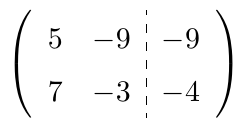
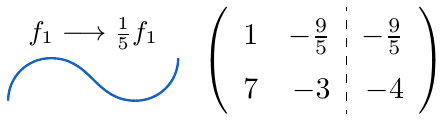
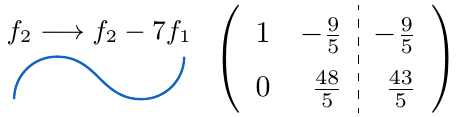
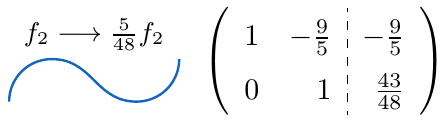
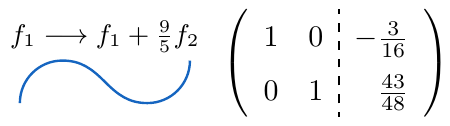
,
.
ecuaciones y
incógnitas. Calcule la solución del mismo usando el Método de Eliminación de Gauss-Jordan.
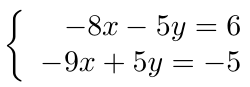
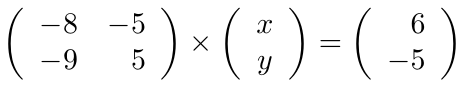
para verificar que éste sea diferente de cero,

es distinto de cero, ampliamos la matriz adosando la matriz
en el lado derecho y aplicamos el Método de Eliminación de Gauss-Jordan sobre la matriz
.
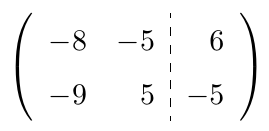



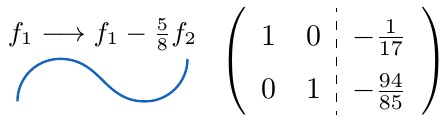
,
.
ecuaciones y
incógnitas. Calcule la solución del mismo usando el Método de Eliminación de Gauss-Jordan.
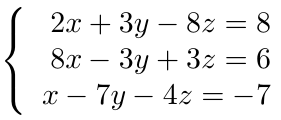
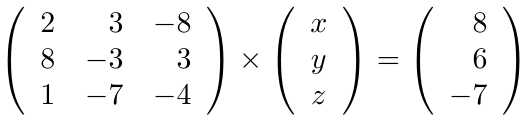
para verificar que éste sea diferente de cero,
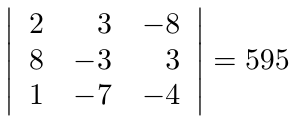
es distinto de cero, ampliamos la matriz adosando la matriz
en el lado derecho y aplicamos el Método de Eliminación de Gauss-Jordan sobre la matriz
.
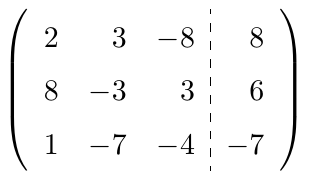
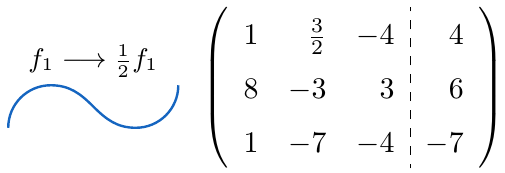
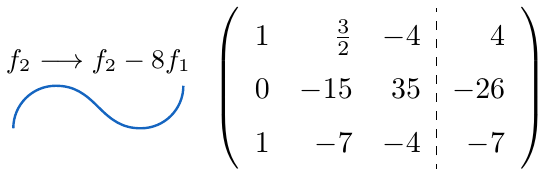
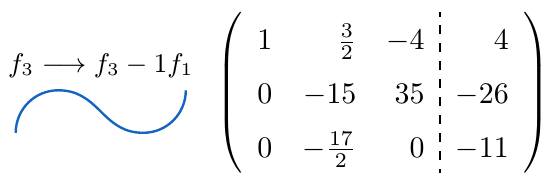
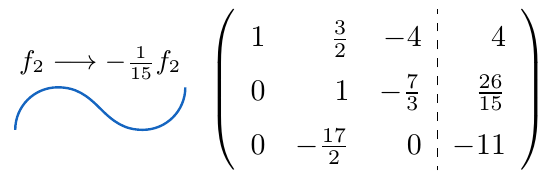

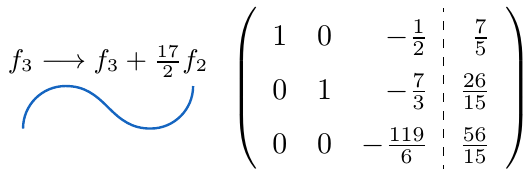
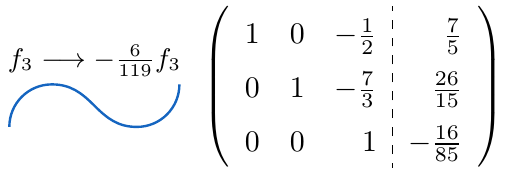
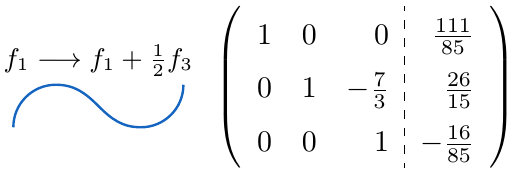
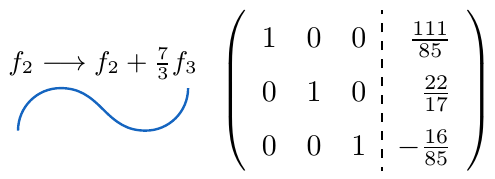
,
,
.
ecuaciones y
incógnitas. Calcule la solución del mismo usando el Método de Eliminación de Gauss-Jordan.

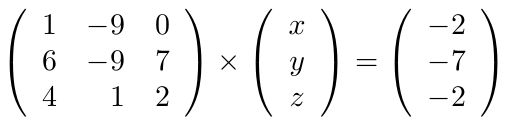
para verificar que éste sea diferente de cero,
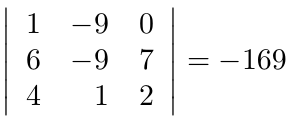
es distinto de cero, ampliamos la matriz adosando la matriz
en el lado derecho y aplicamos el Método de Eliminación de Gauss-Jordan sobre la matriz
.
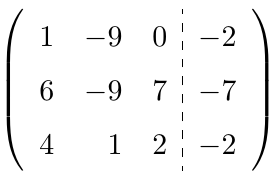
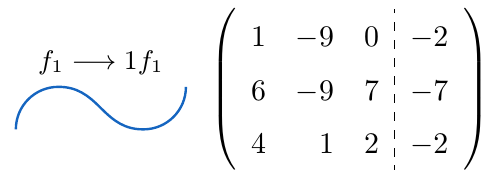
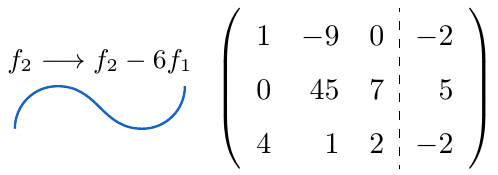
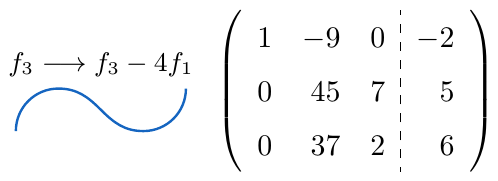
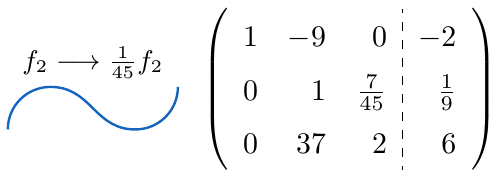
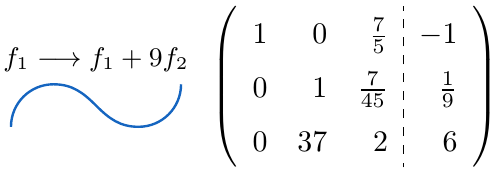
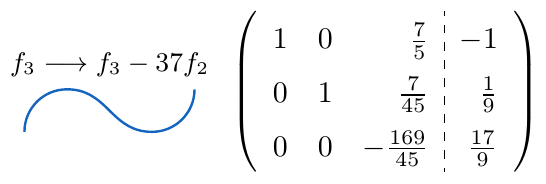
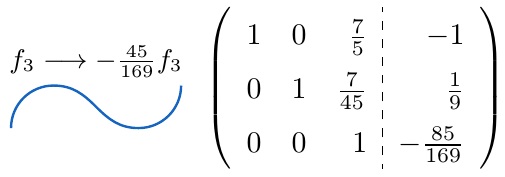
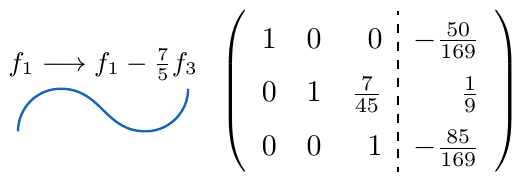
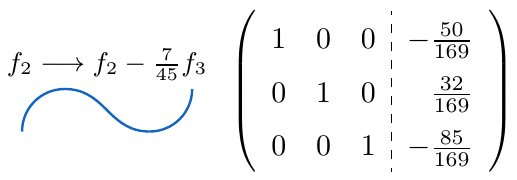
,
,
.
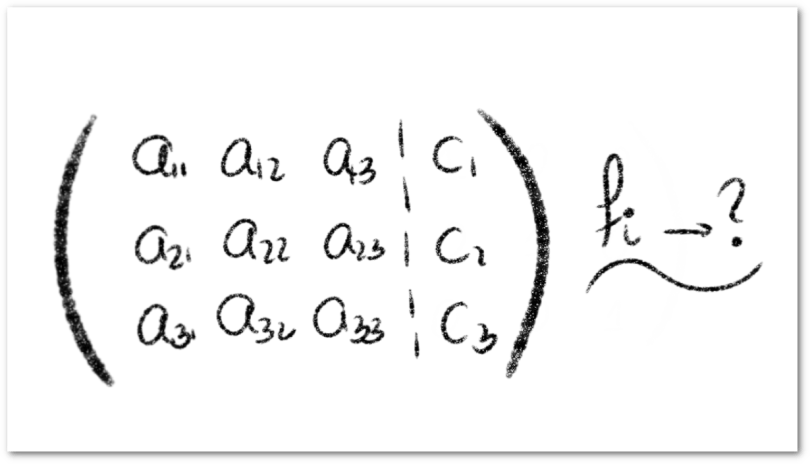















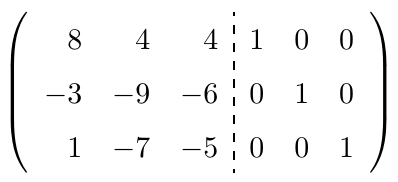









































































































































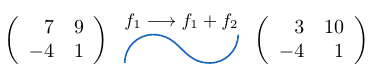
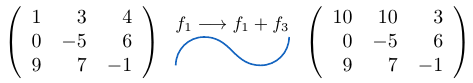
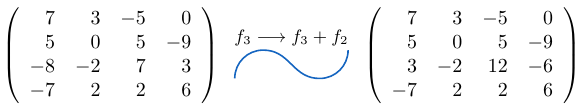
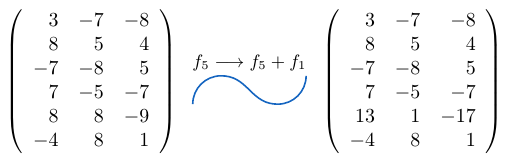
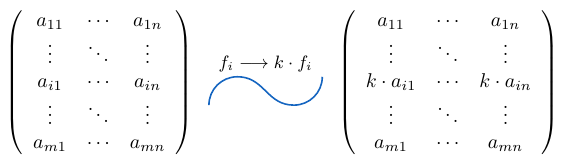
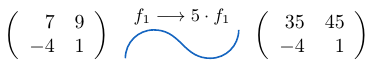
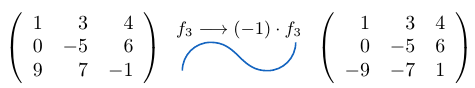

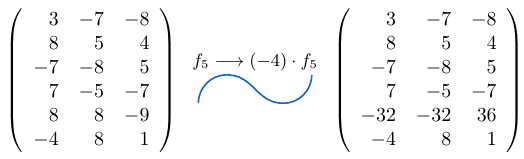
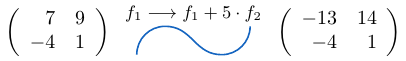
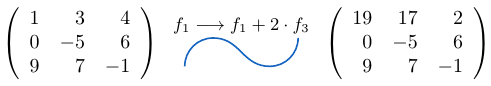
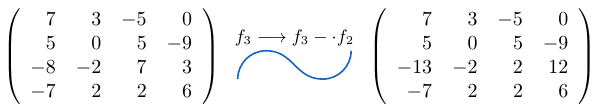
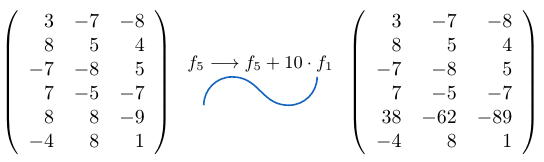
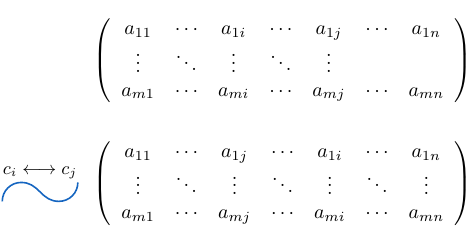


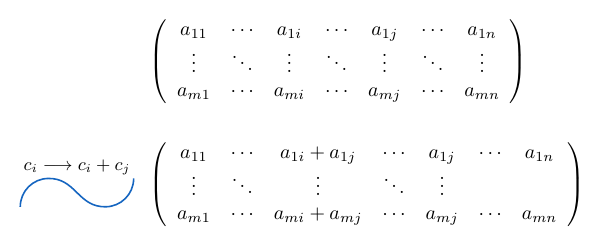
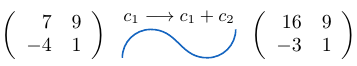
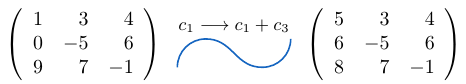





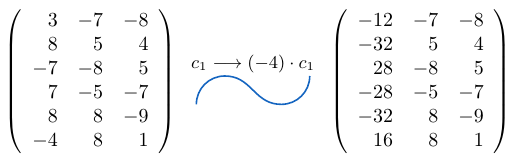
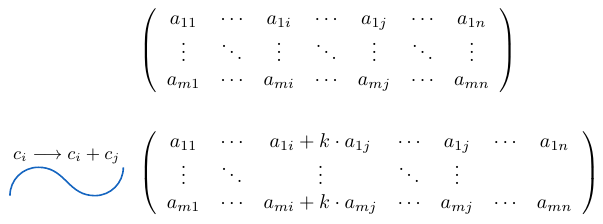
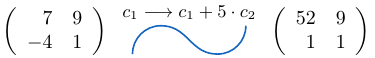
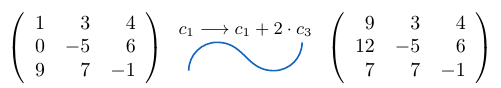

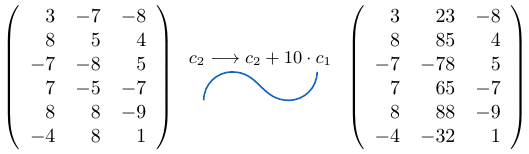
Debe estar conectado para enviar un comentario.