También pudiera interesarte
Menor de una matriz
Si es una matriz cuadrada de tamaño
, es decir, de tamaño
. Para cada elemento
, definimos el menor del elemento
(o la submatriz principal
de
) como la matriz que resulta al eliminar la fila
y la columna
de la matriz
. Lo denotamos como
o
y escrito de forma exhaustiva, tenemos

Cofactor de una matriz
Una vez definidos los menores de una matriz, definimos cofactor del elemento multiplicando
por el determinante del menor del elemento
. Lo denotamos como
o
y escrito de forma exhaustiva, tenemos
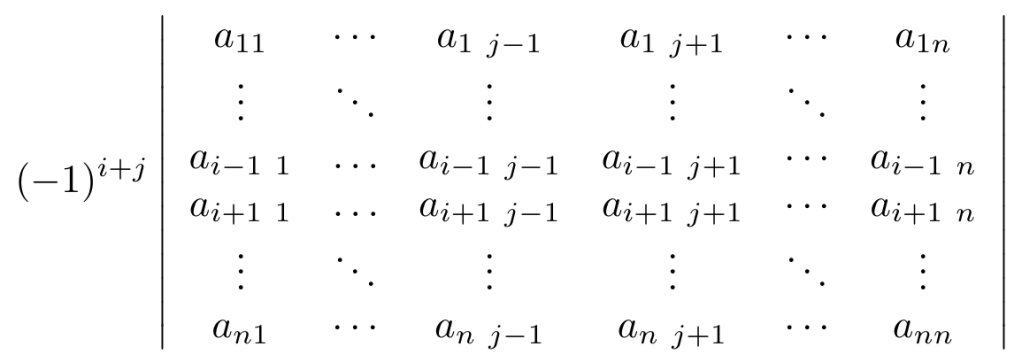
A esta expresión también se le conoce en algunos textos como el adjunto de y se denota como
, y aunque esta expresión luce monstruosamente fea, veamos con algunos ejemplos como calcular los cofactores de una matriz cuadrada de tamaño tres.
A esta expresión también se le conoce en algunos textos como el adjunto de y se denota como
, y aunque esta expresión luce monstruosamente fea, veamos con algunos ejemplos como calcular los cofactores de una matriz cuadrada de tamaño tres.
Ejemplos: Cálculo de cofactores
Ejemplo 1
Considerando la matriz cuadrada de tamaño tres, el cofactor
.


Ejemplo 2
Considerando la matriz cuadrada de tamaño tres, el cofactor
.


Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 3
Considerando la matriz cuadrada de tamaño tres, el cofactor
.


Ejemplo 4
Considerando la matriz cuadrada de tamaño tres, el cofactor
.


Ejemplo 5
Considerando la matriz cuadrada de tamaño tres, el cofactor
.


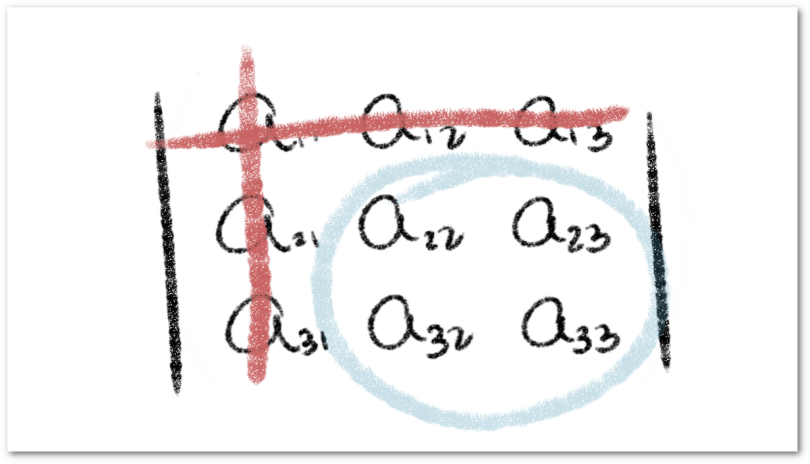
[…] Matemática I – Sección 01 – Semestre B2022 – totumat en Menores y Cofactores […]
Me gustaMe gusta
[…] Menores y Cofactores […]
Me gustaMe gusta