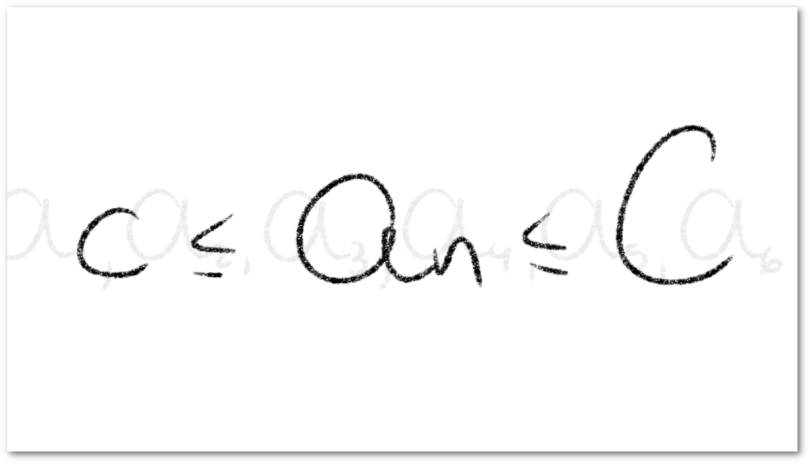Sucesiones

Sucesiones Acotadas

Anthonny Arias-GarcíaDeja un comentario
  1. Cotas Superiores
    1. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2
      3. Ejemplo 3
  2. Cotas Inferiores
    1. Ejemplos
      1. Ejemplo 4
      2. Ejemplo 5
      3. Ejemplo 6
  3. Sucesiones Acotadas

Otro aspecto importante en el estudio de las sucesiones es saber cuales son los elementos que las encajonan, ya que de esta forma, podemos establecer con más claridad el espacio donde estas se desarrollan.

También pudiera interesarte

Anuncios

Cotas Superiores

Una cota superior (o elemento mayorante) de una sucesión es un número real que es mayor o igual que cualquier elemento de la sucesión. Formalmente, C es una cota superior de una sucesión a_n si a_n \leq C para todo número natural n. Si una sucesión tiene una cota superior, diremos que la sucesión está \textbf{acotada superiormente}.

Veamos algunos ejemplos de este tipo de sucesiones:

Ejemplos

Ejemplo 1

Si consideramos la sucesión \left\{ -n \right\}_{n} =\{ -1, -2, -3, -4, -5, -6, \ldots \}, esta sucesión está acotada superiormente, pues si consideramos 1, 0, 9 o 3572; estos valores serán cotas superiores pues son mayores o iguales que cualquier elemento de la sucesión.

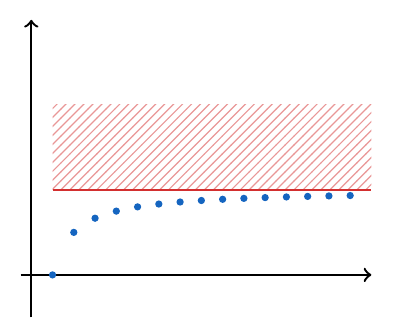
De forma general, podemos decir que cualquier número mayor o igual que -1 es una cota superior de esta sucesión, veamos en el siguiente gráfico una ilustración de esta idea y señalemos en el área rayada el conjunto de las cotas superiores.

Ejemplo 2

Si consideramos la sucesión \left\{ 1 \right\}_{n} =\{ 1, 1, 1, 1, 1, 1, \ldots \}, esta sucesión está acotada superiormente, pues si consideramos 3, 2, 14 o 1000; estos valores serán cotas superiores pues son mayores o iguales que cualquier elemento de la sucesión.

De forma general, podemos decir que cualquier número mayor o igual que 1 es una cota superior de esta sucesión, veamos en el siguiente gráfico una ilustración de esta idea y señalemos en el área rayada el conjunto de las cotas superiores.

Ejemplo 3

Si consideramos la sucesión \left\{ 1-\frac{1}{n} \right\}_{n} =\left\{ 0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \ldots \right\}, esta sucesión está acotada superiormente, pues si consideramos 2, 33, 97 o 751; estos valores serán cotas superiores pues son mayores o iguales que cualquier elemento de la sucesión.

De forma general, podemos decir que cualquier número mayor o igual que 1 es una cota superior de esta sucesión, veamos en el siguiente gráfico una ilustración de esta idea y señalemos en el área rayada el conjunto de las cotas superiores.

Cotas Inferiores

Una cota inferior (o elemento minorante) de una sucesión es un número real que es menor o igual que cualquier elemento de la sucesión. Formalmente, c es una cota superior de una sucesión a_n si a_n \geq c para todo número natural n. Si una sucesión tiene una cota inferior, diremos que la sucesión está \textbf{acotada inferiormente}.

Veamos algunos ejemplos de este tipo de sucesiones:

Ejemplos

Ejemplo 4

Si consideramos la sucesión \left\{ n \right\}_{n} =\{ 1, 2, 3, 4, 5, 6, \ldots \}, esta sucesión está acotada inferiormente, pues si consideramos -1, 0, -34 o 0.5; estos valores serán cotas inferiores pues son menores o iguales que cualquier elemento de la sucesión.

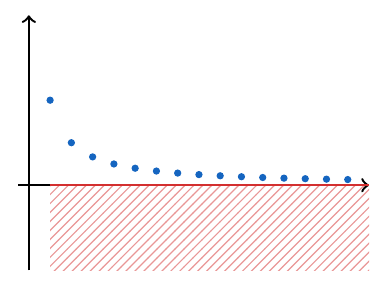
De forma general, podemos decir que cualquier número menor o igual que 1 es una cota inferior de esta sucesión, veamos en el siguiente gráfico una ilustración de esta idea y señalemos en el área rayada el conjunto de las cotas inferiores.

Ejemplo 5

Si consideramos la sucesión \left\{ 3 \right\}_{n} = \{ 3, 3, 3, 3, 3, 3, \ldots \}, esta sucesión está acotada inferiormente, pues si consideramos 2, -839, 1.5 o -55; estos valores serán cotas inferiores pues son menores o iguales que cualquier elemento de la sucesión.

De forma general, podemos decir que cualquier número menor o igual que 3 es una cota inferior de esta sucesión, veamos en el siguiente gráfico una ilustración de esta idea y señalemos en el área rayada el conjunto de las cotas inferiores.

Ejemplo 6

Si consideramos la sucesión \left\{ \frac{1}{n} \right\}_{n} =\left\{ 0, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \ldots \right\}, esta sucesión está acotada inferiormente, pues si consideramos -2, -10, -7.98 o -457; estos valores serán cotas inferiores pues son menores o iguales que cualquier elemento de la sucesión.

De forma general, podemos decir que cualquier número menor o igual que 0 es una cota inferior de esta sucesión, veamos en el siguiente gráfico una ilustración de esta idea y señalemos en el área rayada el conjunto de las cotas inferiores.

Sucesiones Acotadas

De forma general, diremos que una sucesión está acotada si está acotada tanto superior como inferiormente. Formalmente, diremos que una sucesión a_n está acotada si existe un par de números reales r y R tales que r \leq a_n \leq R para todo número natural n. Por ejemplo, si consideramos la sucesión \left\{ (-1)^{n-1} \right\}_{n} =\{ 1, -1, 1, -1, 1, -1, \ldots \} y vemos su comportamiento de forma gráfica:

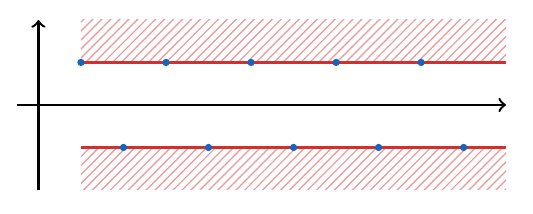
Podemos notar que esta sucesión está acotada superiormente por cualquier número mayor que 1 y está acotada inferiormente por cualquier número menor que -1.

También hay sucesiones que no están acotadas (ni superior ni inferiormente), por ejemplo, si consideramos la sucesión \left\{ n(-1)^{n-1} \right\}_{n} = \{ 1, -2, 3, -4, 5, -6, \ldots\} y viendo su comportamiento de forma gráfica:

Es fácil notar que esta sucesión no está acotada.

¿Tienes alguna duda? Compártela en los comentarios.

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.