Sucesiones

Máximo y Mínimo de una sucesión

Anthonny Arias-GarcíaDeja un comentario
  1. Máximo de una Sucesión
    1. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2
      3. Ejemplo 3
  2. Mínimo de una Sucesión
    1. Ejemplos
      1. Ejemplo 4
      2. Ejemplo 5
      3. Ejemplo 6

Al estudiar las cotas de una sucesión, estos números tenían la libertad de pertenecer o no a la sucesión. A continuación, estudiaremos dos elementos que acotan a la sucesión pero que además, deben estar dentro de la sucesión.

También pudiera interesarte

Anuncios

Máximo de una Sucesión

Diremos que una sucesión tiene el elemento máximo si existe un elemento de la sucesión que es mayor o igual que cualquier elemento de la sucesión. Formalmente, diremos que M es el máximo de una sucesión a_n si M \in \{a_n\}_{n \in \mathbb{N}} y a_n \leq M para todo número natural n. En otras palabras, el máximo de la sucesión es una cota superior que está dentro de la sucesión.

Veamos algunos ejemplos del máximo de una sucesión:

Ejemplos

Ejemplo 1

Si consideramos la sucesión \left\{ -n \right\}_{n} =\{ -1, -2, -3, -4, -5, -6, \ldots \}, tiene máximo, pues si consideramos M=-1, este valor es el elemento más grande de la sucesión. Veamos su comportamiento de forma gráfica:

Ejemplo 2

Si consideramos la sucesión \left\{ 1 \right\}_{n} =\{ 1, 1, 1, 1, 1, 1, \ldots \}, tiene máximo, pues si consideramos M=1, este valor es el elemento más grande de la sucesión. Veamos su comportamiento de forma gráfica:

Ejemplo 3

Si consideramos la sucesión \left\{ 1-\frac{1}{n} \right\}_{n} =\left\{ 0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \ldots \right\}, esta sucesión aunque pareciera acercarse a uno, no tiene máximo. Veamos su comportamiento de forma gráfica:

Lo que podemos notar es que aunque la sucesión es creciente, esta nunca alcanzará un punto máximo.

Anuncios
Anuncios
Anuncios

Mínimo de una Sucesión

Diremos que una sucesión tiene el elemento mínimo si existe un elemento de la sucesión que es menor o igual que cualquier elemento de la sucesión. Formalmente, diremos que m es el mínimo de una sucesión a_n si m \in \{a_n\}_{n \in \mathbb{N}} y a_n \geq m para todo número natural n. En otras palabras, el mínimo de la sucesión es una cota inferior que está dentro de la sucesión.

Veamos algunos ejemplos del máximo de una sucesión:

Ejemplos

Ejemplo 4

Si consideramos la sucesión \left\{ n \right\}_{n} =\{ 1, 2, 3, 4, 5, 6, \ldots \}, tiene mínimo, pues si consideramos m=1, este valor es el elemento más pequeño de la sucesión. Veamos su comportamiento de forma gráfica y señalemos con un punto rojo el elemento máximo de la sucesión.

Ejemplo 5

Si consideramos la sucesión \left\{ 3 \right\}_{n} =\{ 3, 3, 3, 3, 3, 3, \ldots \}, tiene mínimo, pues si consideramos m=3, este valor es el elemento más pequeño de la sucesión. Veamos su comportamiento de forma gráfica y señalemos con un punto rojo el elemento máximo de la sucesión.

Ejemplo 6

Si consideramos la sucesión \left\{ \frac{1}{n} \right\}_{n} =\left\{ 0, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \ldots \right\}, esta sucesión aunque pareciera acercarse a cero, no tiene mínimo. Veamos su comportamiento de forma gráfica para ilustrar esta idea:

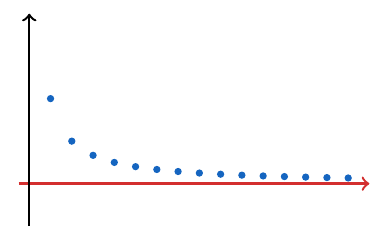
Lo que podemos notar es que aunque la sucesión es decreciente, esta nunca alcanzará un punto mínimo.

¿Tienes alguna duda? Compártela en los comentarios.

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.