Al estudiar las cotas de una sucesión, existen elementos que acotan a la sucesión con mayor rigurosidad que cualquier otra cota, estos son conocidos como el ínfimo y el supremo, veamos como están definidos y como identificarlos.
Supremo de una Sucesión
Si una sucesión está acotada superiormente, diremos que el supremo de esta sucesión es la menor de las cotas superiores, o en otras palabras, es el mínimo del conjunto de todas sus cotas superiores. Formalmente, diremos que una cota superior 
Veamos algunos ejemplos del supremo de una sucesión:
Ejemplos
Ejemplo 1
Si consideramos la sucesión 
En este caso particular, el supremo coincide con el máximo de la sucesión.
Ejemplo 2
Si consideramos la sucesión 
En este caso particular, el supremo coincide con el máximo de la sucesión.
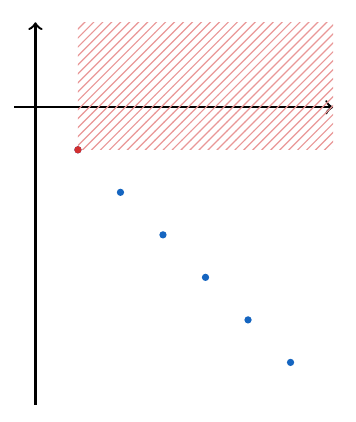
Ejemplo 3
Si consideramos la sucesión 
Notemos que en este caso, la sucesión no tiene máximo, sin embargo, sí tiene supremo pues toda sucesión acotada superiormente, tiene supremo. Lo hemos señalado con una línea roja.
Ínfimo de una Sucesión
Si una sucesión está acotada inferiormente, diremos que el ínfimo de esta sucesión es la mayor de las cotas inferiores, o en otras palabras, es el máximo del conjunto de todas sus cotas inferiores. Formalmente, diremos que una cota inferior $c_0$ es el ínfimo de una sucesión 
Veamos algunos ejemplos del supremo de una sucesión:
Ejemplos
Ejemplo 4
Si consideramos la sucesión 
En este caso particular, el ínfimo coincide con el mínimo de la sucesión.
Ejemplo 5
Si consideramos la sucesión 
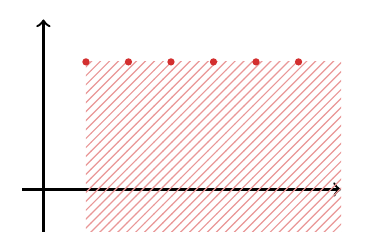
En este caso particular, el ínfimo coincide con el mínimo de la sucesión.
Ejemplo 6
Si consideramos la sucesión 
Notemos que en este caso, la sucesión no tiene mínimo, sin embargo, sí tiene ínfimo pues toda sucesión acotada inferiormente, tiene ínfimo. Lo hemos señalado con una línea roja.
totumat 