Suponga que usted va al supermercado a comprar víveres semanalmente, y ve que un kilo de tomates tiene un precio de Ps., le parece costoso pero decide llevar un kilo pues los necesita para cocinar. La semana siguiente vuelve al supermercado y ve que un kilo de tomates tiene un precio de
Ps, considerando que está en la mitad del precio de la semana anterior, usted decide llevar tres kilos.
También pudiera interesarte
Esta situación se presenta de forma general, pues al considerar el precio de un artículo, los consumidores comprarán menos unidades del artículo cuando el precio es alto y comprarán más unidades del artículo cuando el precio es bajo, esto se conoce como la demanda de un artículo.
Entonces, si bien podemos intuir que la demanda de un artículo disminuye a medida que el precio del artículo aumenta, nuestro propósito será el de determinar la forma cuantificable esta relación.
La Curva de Demanda
Para esto, definimos un plano cartesiano cuyos ejes están definidos por la variable precio, denotada por y la variable cantidad, denotada por
; para mantener la simplicidad de los modelos, consideraremos una economía simple, es decir, tal que las variables
y
sólo pueden tener valores positivos. De esta forma, nos ubicaremos sólo en el primer cuadrante del plano cartesiano.

Veamos en los siguientes ejemplos, cómo conociendo la demanda y el precio de un artículo en un momento determinado, podemos definir rectas que describen de forma general la demanda del artículo.
Ejemplos
Ejemplo 1
Suponga que la demanda diaria de zanahoria en una pequeña tienda de verduras de la ciudad es de kilo cuando el precio es de
Ps. por kilo, y de
kilos cuando el precio es de
Ps. por kilo. ¿Cuál es la ecuación general de la recta que define la relación entre el precio y la demanda? ¿Cuál será la cantidad demandada si fija el precio en
Ps.?
Debemos considerar que si la demanda es de 1 kilo cuando el precio es de Ps., podemos representar esta información como un punto
el plano cartesiano donde
y
, es decir, el punto
; de igual forma, si la demanda es de
kilos cuando el precio es de
Ps., podemos representar esta información con el punto
.
De esta forma, si contamos con estos dos puntos, podemos calcular la recta que pasa por estos dos usando la ecuación punto-punto. Entonces, si y
son dos puntos en el plano cartesiano, calculamos el valor de la pendiente,
Posteriormente aplicamos la ecuación punto-pendiente, escogiendo el punto de nuestra preferencia. Usemos el punto
La recta que pasa por los puntos y
es llamada la Ecuación de Demanda de zanahoria. Este tipo de ecuaciones siempre tendrá pendiente negativa y su gráfica será una recta decreciente.

Para determinar cuál será la cantidad demandada si se fija el precio en Ps. debemos considerar la ecuación de demanda y sustituir el valor
en ella, posteriormente se despeja la variable
, de la siguiente forma
Por lo tanto, la demanda de zanahoria será de kilos diarios si se fija el precio en
Ps.
Ejemplo 2
Suponga que la demanda mensual de zapatos para dama en una zapatería es de pares cuando el precio es de
Ps. por par, y de
pares cuando el precio es de
Ps. por par. ¿Cuál es la ecuación general de la recta que define la relación entre el precio y la demanda? ¿Cuál será la cantidad demandada si fija el precio en
Ps.?
Debemos considerar que si la demanda es de pares cuando el precio es de
Ps., podemos representar esta información con el punto
; de igual forma, si la demanda es de
pares cuando el precio es de
Ps., podemos representar esta información con el punto
.
De esta forma, si contamos con estos dos puntos, podemos calcular la recta que pasa por estos dos usando la ecuación punto-punto. Entonces, si y
son dos puntos en el plano cartesiano, calculamos el valor de la pendiente,
Posteriormente aplicamos la ecuación punto-pendiente, escogiendo el punto de nuestra preferencia. Usemos el punto
La recta que pasa por los puntos y
es llamada la Ecuación de Demanda de zapatos para dama. Este tipo de ecuaciones siempre tendrá pendiente negativa y su gráfica será una recta decreciente.

Para determinar cual será la cantidad demandada si se fija el precio en Ps. debemos considerar la ecuación de demanda y sustituir el valor
en ella, posteriormente se despeja la variable
, de la siguiente forma
Por lo tanto, la demanda de zapatos para damas será de aproximadamente pares mensuales si se fija el precio en
Ps.
Debemos notar que en ambos ejemplos, las rectas que definen la demanda tienen pendiente negativa y en consecuencia, son rectas decrecientes. Entonces concluimos que de forma general, si , cualquier ecuación de demanda tiene la forma
Ejercicios propuestos por los usuarios de totumat
Ejercicio 1
¿Me podrían ayudar a resolver el siguiente problema?
El equilibrio de mercado para un producto ocurre cuando se fabrican 13500 unidades a un precio de $45 por unidad, El fabricante no hace oferta de unidades con precio $10 y los consumidores no demandan unidades con precio $200.
- Obtener la ecuación de demanda si se supone lineal.
- Determinar el precio por unidad cuando se demandan 5000 unidades.
Gracias,
Mary.
Respuesta:
Lo primero que debemos hacer al abordar problemas de este tipo es identificar cuales son los elementos que se presentan para reescribirlos en lenguaje matemático. Estos son:
- El punto de equilibrio:
.
- El fabricante no ofrece cuando el precio es de $10: Este es el punto
.
- Los consumidores no demandan cuando el precio es de $200: Este es el punto
.
Como se supone que la demanda es lineal, debemos calcular la ecuación de la recta que pasa por los puntos y
. Para esto aplicamos la ecuación punto-punto:
Esta última ecuación es la ecuación lineal de demanda y para determinar el precio por unidad cuando se demandan 5000 unidades, basta con sustituir en la ecuación, esto es:
Ejercicio 2
Hola, ¿me podría ayudar con este ejercicio? Obtengo como resultado
q = p/-2
No sé si estoy resolviéndolo bien.
El enunciado del ejercicio es el siguiente: Cuando el precio de los relojes es de $1000 dólares, no hay demanda alguna; cuando es gratuito en el mercado se demandan 500 relojes; ¿Cuál es la ecuación de la demanda? Grafique y explique; ¿cuál es el precio techo que se puede vender en el mercado?
Muchas gracias.
Respuesta:
Lo primero que debemos hacer al abordar problemas de este tipo es identificar cuales son los elementos que se presentan para reescribirlos en lenguaje matemático. Estos son:
- Cuando el precio de los relojes es de $1000 dólares, no hay demanda alguna: Este es el punto
.
- Cuando es gratuito en el mercado se demandan 500 relojes: Este es el punto
.
Como se supone que la demanda es lineal, debemos calcular la ecuación de la recta que pasa por los puntos y
. Para esto aplicamos la ecuación punto-punto:
Posteriormente, podemos hacer un despeje para expresar esta ecuación como en función de
, para obtener la siguiente ecuación:
Esta última ecuación se puede apreciar gráficamente:



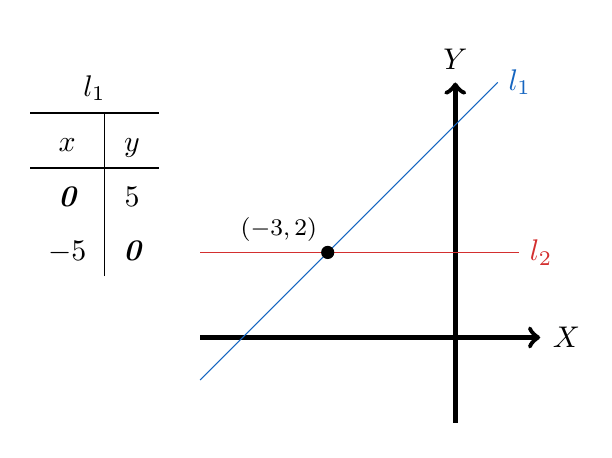
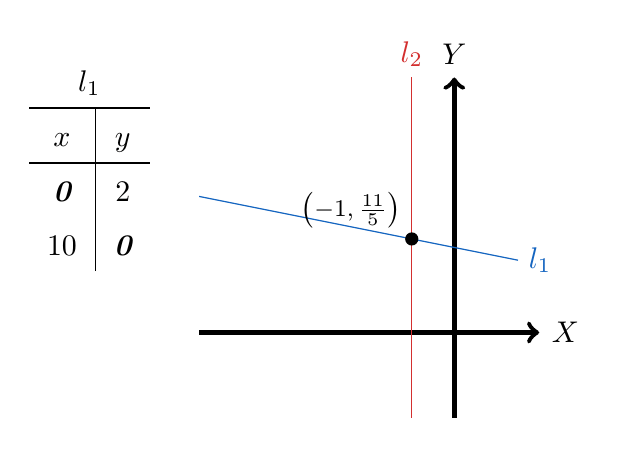
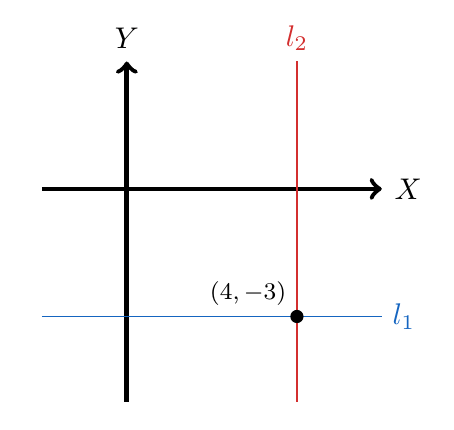
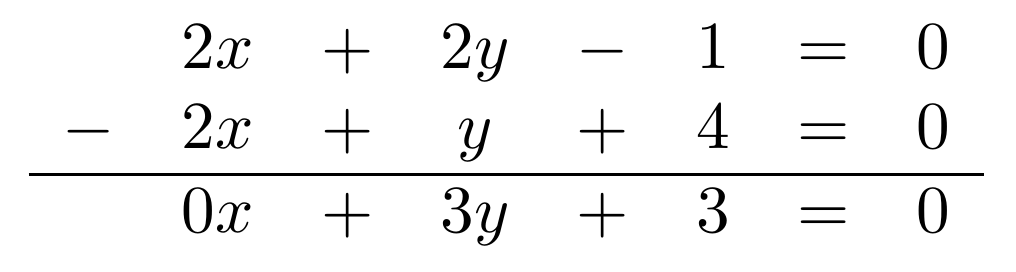
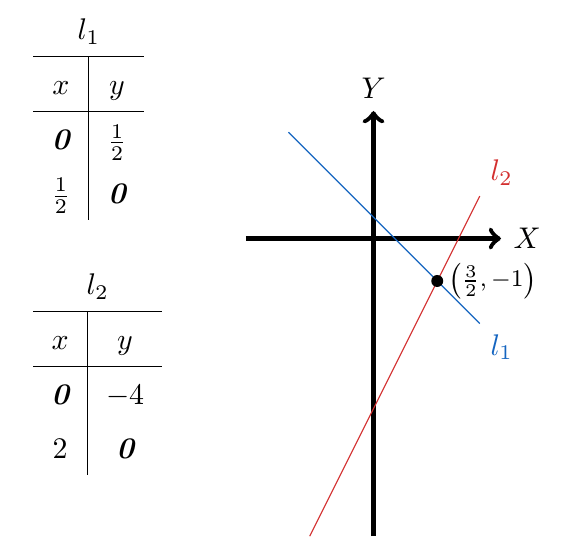
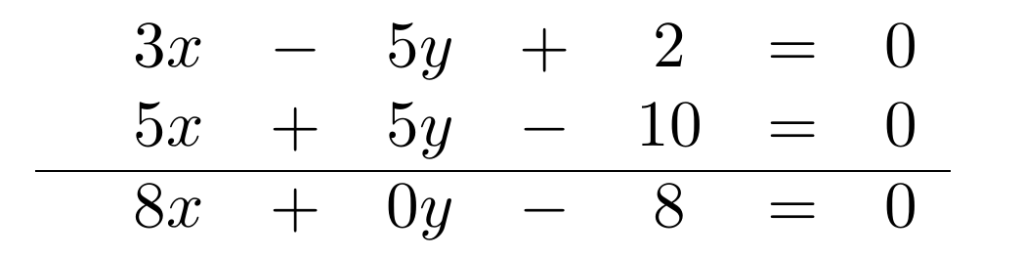
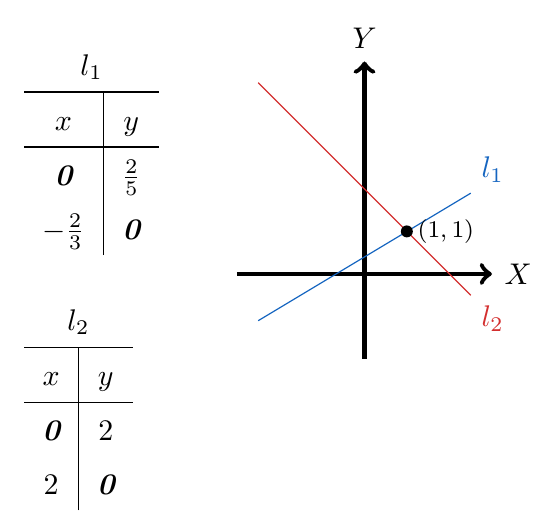
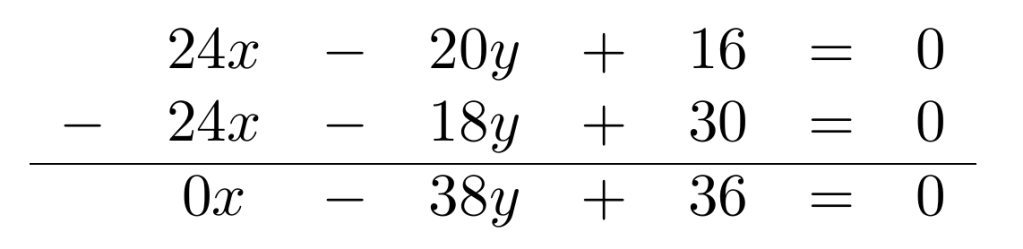
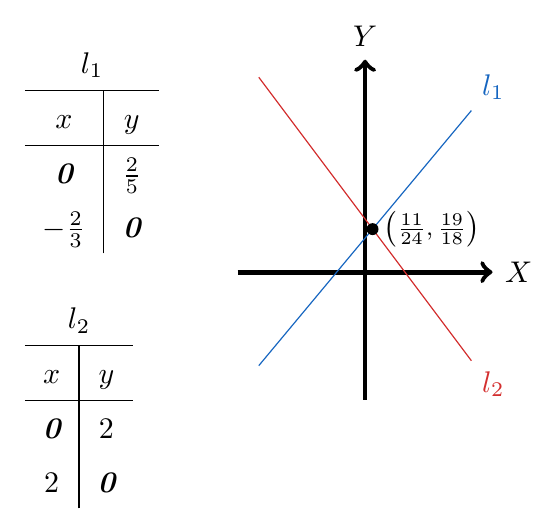
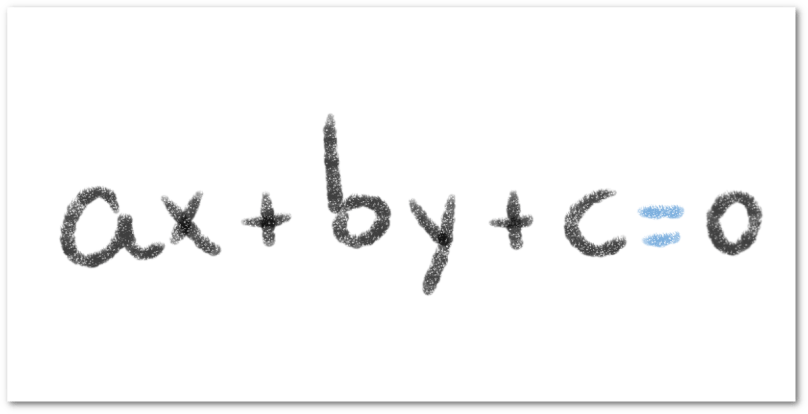
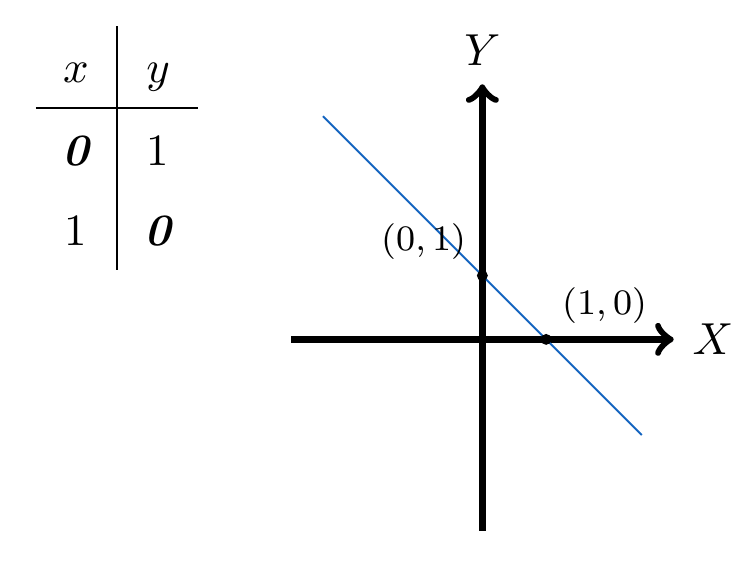
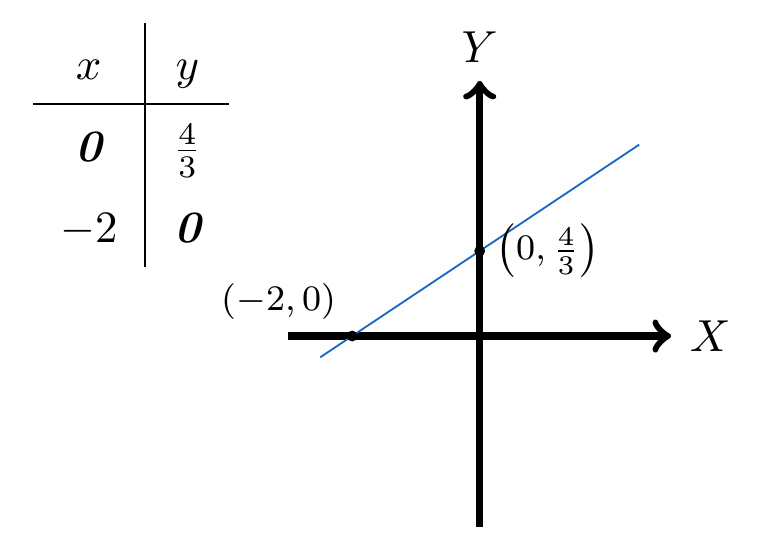





Debe estar conectado para enviar un comentario.