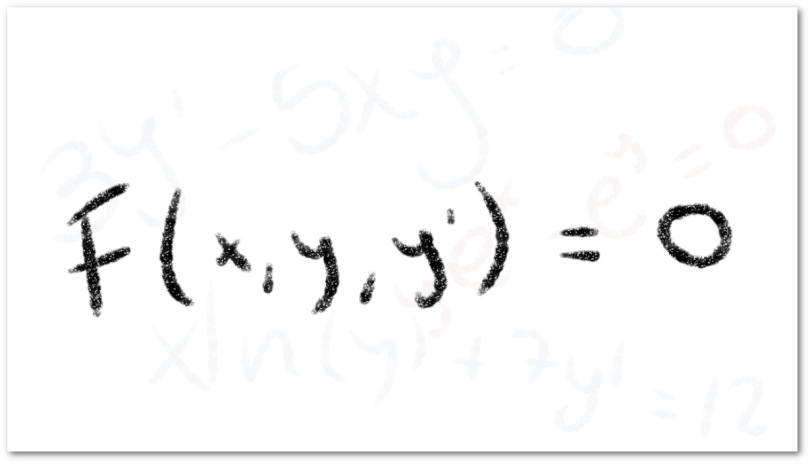El conjunto de todas las ecuaciones diferenciales es bastante amplio, es por esto que empezaremos su estudio desarrollando algunas de las técnicas para calcular la solución de ecuaciones diferenciales ordinarias de primer orden, así que empecemos por definir este tipo de ecuaciones. Formalmente diremos que este tipo de ecuaciones se expresa de la siguiente forma
Antes de abordar las técnicas básicas para calcular la solución de este tipo de ecuaciones diferenciales, veamos algunos ejemplos para aprender a identificarlas.
Ejemplos
Ejemplo 1
La ecuación diferencial involucra sólo una variable independiente y la derivada de mayor orden involucrada es de primer orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria de primer orden.
Ejemplo 2
La ecuación diferencial involucra sólo una variable independiente y la derivada de mayor orden involucrada es de primer orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria de primer orden.
Ejemplo 3
La ecuación diferencial involucra sólo una variable independiente y la derivada de mayor orden involucrada es de primer orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria de primer orden.
Ejemplo 4
La ecuación diferencial involucra sólo una variable independiente y la derivada de mayor orden involucrada es de primer orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria de primer orden.
Ejemplo 5
La ecuación diferencial involucra sólo una variable independiente y la derivada de mayor orden involucrada es de primer orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria de primer orden.