- Notación
- Regla de la suma
- Ejemplos
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
- Ejemplo 4
- Regla del producto por un escalar
- Ejemplos
- Ejemplo 5
- Ejemplo 6
- Ejemplo 7
- Ejemplo 8
- Regla del producto
- Ejemplos
- Ejemplo 9
- Ejemplo 10
- Ejemplo 11
- Ejemplo 12
- Regla de la división
- Ejemplos
- Ejemplo 13
- Ejemplo 14
- Ejemplo 15
- Ejemplo 16
Notación
Dependiendo del contexto, es necesario usar diferentes notaciones para la derivada. Por defecto, si queremos calcular la derivada de una función explícitamente definida como  , usamos la notación
, usamos la notación  .
.
Sin embargo, al derivar la expresión que define a la función, puede resultar necesario usar otro tipo de notación como sigue:
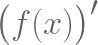
También podemos recurrir a la definición propiamente de lo que es una derivada para denotarla. Recordemos que formalmente la derivada de una función es una razón de cambio puntual, es decir, el cambio en el Eje Y entre el cambio en el Eje X.
Pero al calcular el límite cuando  tiende a
tiende a 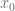 estos cambios se hacen infinitamente pequeños, a estos cambios los llamamos diferenciales, al cambio infinitamente pequeño en el Eje Y lo llamamos diferencial de y y lo denotamos por
estos cambios se hacen infinitamente pequeños, a estos cambios los llamamos diferenciales, al cambio infinitamente pequeño en el Eje Y lo llamamos diferencial de y y lo denotamos por 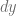 ; al cambio infinitamente pequeño en el Eje X lo llamamos diferencial de x y lo denotamos por
; al cambio infinitamente pequeño en el Eje X lo llamamos diferencial de x y lo denotamos por  .
.
Es por esto, que la derivada de una función se expresa como un cociente de diferenciales de la siguiente manera:

Esta notación se lee la derivada de  respecto a
respecto a  .
.
Particularmente, si la variable  está definida de forma pendiente a través de una función
está definida de forma pendiente a través de una función  entonces usamos la notación
entonces usamos la notación

También pudiera interesarte
Una vez que hemos determinado la derivada de las funciones elementales, considerando la definición de derivada, es posible deducir la derivada de las operaciones básicas entre funciones. Formalmente, si  y
y  son dos funciones; y
son dos funciones; y  es un número real, definimos las siguientes reglas:
es un número real, definimos las siguientes reglas:
Regla de la suma
Si  y
y  son dos funciones, definimos la derivada de la suma, como la suma de las derivadas, es decir,
son dos funciones, definimos la derivada de la suma, como la suma de las derivadas, es decir,

Ejemplos
Ejemplo 1
Considerando la función  , calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:

Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas
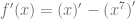
Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que

Ejemplo 2
Considerando la función  , calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:

Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas
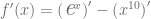
Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que

Ejemplo 3
Considerando la función  , calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:

Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas

Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
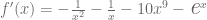
Ejemplo 4
Considerando la función  , calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la suma. Para esto, denotamos primero la derivada:

Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas
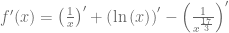
Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Regla del producto por un escalar
Si  es una función y si
es una función y si  es un escalar, definimos la derivada de un escalar multiplicado por una función como dicho escalar multiplicado por la derivada de la función, es decir,
es un escalar, definimos la derivada de un escalar multiplicado por una función como dicho escalar multiplicado por la derivada de la función, es decir,

Nota: Diremos que un número real  es un escalar, porque cambia la escala de la función, pues dependiendo de su valor, puede contraerla o expandirla.
es un escalar, porque cambia la escala de la función, pues dependiendo de su valor, puede contraerla o expandirla.
Ejemplos
Ejemplo 5
Considerando la función  , calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:
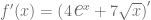
Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas

Una vez que hemos separado los sumandos, podemos sacar los escalares de cada uno de estos sumandos

Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
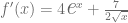
Ejemplo 6
Considerando la función  , calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:

Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas
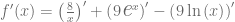
Una vez que hemos separado los sumandos, podemos sacar los escalares de cada uno de estos sumandos

Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
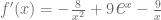
Ejemplo 7
Considerando la función  , calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:

Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas
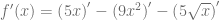
Una vez que hemos separado los sumandos, podemos sacar los escalares de cada uno de estos sumandos

Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
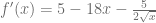
Ejemplo 8
Considerando la función ![f(x)=\frac{9}{x} - 8 \sqrt[9]{x} - 6 \sqrt{x} - 4\textit{\Large e}^{x}](https://s0.wp.com/latex.php?latex=f%28x%29%3D%5Cfrac%7B9%7D%7Bx%7D+-+8+%5Csqrt%5B9%5D%7Bx%7D+-+6+%5Csqrt%7Bx%7D+-+4%5Ctextit%7B%5CLarge+e%7D%5E%7Bx%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) , calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto por un escalar. Para esto, denotamos primero la derivada:
![f'(x)=\left( \frac{9}{x} - 8 \sqrt[9]{x} - 6 \sqrt{x} - 4\textit{\Large e}^{x} \right)'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%28+%5Cfrac%7B9%7D%7Bx%7D+-+8+%5Csqrt%5B9%5D%7Bx%7D+-+6+%5Csqrt%7Bx%7D+-+4%5Ctextit%7B%5CLarge+e%7D%5E%7Bx%7D+%5Cright%29%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como la suma funciones elementales, entonces podemos separar cada uno de los sumandos y expresar sus derivadas
![f'(x)=\left( \frac{9}{x} \right)' - \left( 8 \sqrt[9]{x} \right)' - \left( 6 \sqrt{x} \right)' - \left( 4\textit{\Large e}^{x} \right)'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%28+%5Cfrac%7B9%7D%7Bx%7D+%5Cright%29%27+-+%5Cleft%28+8+%5Csqrt%5B9%5D%7Bx%7D+%5Cright%29%27+-+%5Cleft%28+6+%5Csqrt%7Bx%7D+%5Cright%29%27+-+%5Cleft%28+4%5Ctextit%7B%5CLarge+e%7D%5E%7Bx%7D+%5Cright%29%27+&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Una vez que hemos separado los sumandos, podemos sacar los escalares de cada uno de estos sumandos
![f'(x)=9 \left( \frac{1}{x} \right)' - 8 \left( \sqrt[9]{x} \right)' - 6 \left( \sqrt{x} \right)' - 4 \left( \textit{\Large e}^{x} \right)'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D9+%5Cleft%28+%5Cfrac%7B1%7D%7Bx%7D+%5Cright%29%27+-+8+%5Cleft%28+%5Csqrt%5B9%5D%7Bx%7D+%5Cright%29%27+-+6+%5Cleft%28+%5Csqrt%7Bx%7D+%5Cright%29%27+-+4+%5Cleft%28+%5Ctextit%7B%5CLarge+e%7D%5E%7Bx%7D+%5Cright%29%27+&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Finalmente, consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
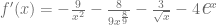
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Regla del producto
Si  y
y  son dos funciones, considerando ambos factores, definimos la derivada de la siguiente forma:
son dos funciones, considerando ambos factores, definimos la derivada de la siguiente forma:
la derivada del primero, por el segundo sin derivar, más, el primero sin derivar, por la derivada del segundo

Ejemplos
Ejemplo 9
Considerando la función  , calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
![f'(x)=\left[ \left( - 5 \sqrt{x} \right) \cdot \left( - 3 \ln{\left(x \right)} \right) \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+%5Cleft%28+-+5+%5Csqrt%7Bx%7D+%5Cright%29+%5Ccdot+%5Cleft%28+-+3+%5Cln%7B%5Cleft%28x+%5Cright%29%7D+%5Cright%29+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como el producto de dos funciones, aplicamos la regla del producto y expresamos las derivadas

Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que

Finalmente, simplificamos para obtener el siguiente el resultado
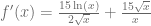
Ejemplo 10
Considerando la función  , calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
![f'(x)=\left[ 6 x \cdot \left( - 9 \ln{\left(x \right)} \right) \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+6+x+%5Ccdot+%5Cleft%28+-+9+%5Cln%7B%5Cleft%28x+%5Cright%29%7D+%5Cright%29+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como el producto de dos funciones, aplicamos la regla del producto y expresamos las derivadas
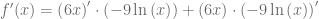
Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que

Finalmente, simplificamos para obtener el siguiente el resultado

Ejemplo 11
Considerando la función  , calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
![f'(x)=\left[ - 3 \textit{\Large e}^{x} \cdot 6 x^{4} \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+-+3+%5Ctextit%7B%5CLarge+e%7D%5E%7Bx%7D+%5Ccdot+6+x%5E%7B4%7D+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como el producto de dos funciones, aplicamos la regla del producto y expresamos las derivadas

Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que

Finalmente, simplificamos para obtener el siguiente el resultado

Ejemplo 12
Considerando la función  , calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para el producto. Para esto, denotamos primero la derivada:
![f'(x)=\left[ -8 \textit{\Large e}^{x} \cdot \frac{6}{x} \cdot \left( - 5 \ln{\left(x \right)} \right) \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+-8+%5Ctextit%7B%5CLarge+e%7D%5E%7Bx%7D+%5Ccdot+%5Cfrac%7B6%7D%7Bx%7D+%5Ccdot+%5Cleft%28+-+5+%5Cln%7B%5Cleft%28x+%5Cright%29%7D+%5Cright%29+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como el producto de dos funciones, aplicamos la regla del producto y expresamos las derivadas
Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
Finalmente, simplificamos para obtener el siguiente el resultado
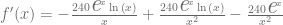
Nota: En este último caso hemos generalizado la regla del producto, y es que si tenemos tres funciones  ,
,  y
y  , es posible deducir que
, es posible deducir que

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Regla de la división
Si  y
y  son dos funciones, considerando el numerador y el denominador, definimos la derivada de la siguiente forma:
son dos funciones, considerando el numerador y el denominador, definimos la derivada de la siguiente forma:
la derivada del numerador, por el denominador sin derivar, menos, el numerador sin derivar, por la derivada del denominador. Todo eso dividido entre el denominador elevado al cuadrado

Ejemplos
Ejemplo 13
Considerando la función 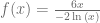 , calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
![f'(x)=\left[ \frac{ 6 x }{ - 2 \ln{\left(x \right)}} \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+%5Cfrac%7B+6+x+%7D%7B+-+2+%5Cln%7B%5Cleft%28x+%5Cright%29%7D%7D+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como la división dos funciones, aplicamos al regla de la división y expresamos las derivadas

Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
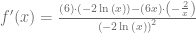
Finalmente, simplificamos para obtener el siguiente el resultado
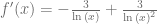
Ejemplo 14
Considerando la función ![f(x)= \frac{ \frac{7}{x} }{ \sqrt[6]{x} }](https://s0.wp.com/latex.php?latex=f%28x%29%3D+%5Cfrac%7B+%5Cfrac%7B7%7D%7Bx%7D+%7D%7B+%5Csqrt%5B6%5D%7Bx%7D+%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) , calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
![f'(x)=\left[ \frac{ \frac{7}{x} }{ \sqrt[6]{x}} \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+%5Cfrac%7B+%5Cfrac%7B7%7D%7Bx%7D+%7D%7B+%5Csqrt%5B6%5D%7Bx%7D%7D+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como la división dos funciones, aplicamos al regla de la división y expresamos las derivadas
![f'(x)= \frac{\left( \frac{7}{x} \right)' \cdot \left( \sqrt[6]{x} \right) - \left( \frac{7}{x} \right) \cdot \left( \sqrt[6]{x} \right)'}{\left( \sqrt[6]{x} \right)^2}](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D+%5Cfrac%7B%5Cleft%28+%5Cfrac%7B7%7D%7Bx%7D+%5Cright%29%27+%5Ccdot+%5Cleft%28+%5Csqrt%5B6%5D%7Bx%7D+%5Cright%29+-+%5Cleft%28+%5Cfrac%7B7%7D%7Bx%7D+%5Cright%29+%5Ccdot+%5Cleft%28+%5Csqrt%5B6%5D%7Bx%7D+%5Cright%29%27%7D%7B%5Cleft%28+%5Csqrt%5B6%5D%7Bx%7D+%5Cright%29%5E2%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
![f'(x)= \frac{\left( - \frac{7}{x^{2}} \right) \cdot \left( \sqrt[6]{x} \right) - \left( \frac{7}{x} \right) \cdot \left( \frac{1}{6 x^{\frac{5}{6}}} \right)}{\left( \sqrt[6]{x} \right)^2}](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D+%5Cfrac%7B%5Cleft%28+-+%5Cfrac%7B7%7D%7Bx%5E%7B2%7D%7D+%5Cright%29+%5Ccdot+%5Cleft%28+%5Csqrt%5B6%5D%7Bx%7D+%5Cright%29+-+%5Cleft%28+%5Cfrac%7B7%7D%7Bx%7D+%5Cright%29+%5Ccdot+%5Cleft%28+%5Cfrac%7B1%7D%7B6+x%5E%7B%5Cfrac%7B5%7D%7B6%7D%7D%7D+%5Cright%29%7D%7B%5Cleft%28+%5Csqrt%5B6%5D%7Bx%7D+%5Cright%29%5E2%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Finalmente, simplificamos para obtener el siguiente el resultado
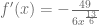
Ejemplo 15
Considerando la función 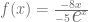 , calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
![f'(x)=\left[ \frac{ - 8 x }{ - 5 \textit{\Large e}^{x} } \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+%5Cfrac%7B+-+8+x+%7D%7B+-+5+%5Ctextit%7B%5CLarge+e%7D%5E%7Bx%7D+%7D+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como la división dos funciones, aplicamos al regla de la división y expresamos las derivadas

Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
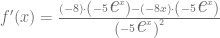
Finalmente, simplificamos para obtener el siguiente el resultado
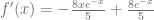
Ejemplo 16
Considerando la función ![f(x)= \frac{ \sqrt[10]{x} }{ - 3 x^{5} }](https://s0.wp.com/latex.php?latex=f%28x%29%3D+%5Cfrac%7B+%5Csqrt%5B10%5D%7Bx%7D+%7D%7B+-+3+x%5E%7B5%7D+%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) , calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
, calcule su derivada aplicando la regla de derivación para la división. Para esto, denotamos primero la derivada:
![f'(x)=\left[ \frac{ \sqrt[10]{x} }{ - 3 x^{5} } \right]'](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D%5Cleft%5B+%5Cfrac%7B+%5Csqrt%5B10%5D%7Bx%7D+%7D%7B+-+3+x%5E%7B5%7D+%7D+%5Cright%5D%27&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Debemos notar que esta función está definida como la división dos funciones, aplicamos al regla de la división y expresamos las derivadas
![f'(x)= \frac{\left( \sqrt[10]{x} \right)' \cdot \left( - 3 x^{5} \right) - \left( \sqrt[10]{x} \right) \cdot \left( - 3 x^{5} \right)'}{\left( - 3 x^{5} \right)^2}](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D+%5Cfrac%7B%5Cleft%28+%5Csqrt%5B10%5D%7Bx%7D+%5Cright%29%27+%5Ccdot+%5Cleft%28+-+3+x%5E%7B5%7D+%5Cright%29+-+%5Cleft%28+%5Csqrt%5B10%5D%7Bx%7D+%5Cright%29+%5Ccdot+%5Cleft%28+-+3+x%5E%7B5%7D+%5Cright%29%27%7D%7B%5Cleft%28+-+3+x%5E%7B5%7D+%5Cright%29%5E2%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Consultamos la tabla de derivadas y calculamos las derivadas respectivas para obtener que
![f'(x)= \frac{\left( \frac{1}{10 x^{\frac{9}{10}}} \right) \cdot \left( - 3 x^{5} \right) - \left( \sqrt[10]{x} \right) \cdot \left( - 15 x^{4} \right)}{\left( - 3 x^{5} \right)^2}](https://s0.wp.com/latex.php?latex=f%27%28x%29%3D+%5Cfrac%7B%5Cleft%28+%5Cfrac%7B1%7D%7B10+x%5E%7B%5Cfrac%7B9%7D%7B10%7D%7D%7D+%5Cright%29+%5Ccdot+%5Cleft%28+-+3+x%5E%7B5%7D+%5Cright%29+-+%5Cleft%28+%5Csqrt%5B10%5D%7Bx%7D+%5Cright%29+%5Ccdot+%5Cleft%28+-+15+x%5E%7B4%7D+%5Cright%29%7D%7B%5Cleft%28+-+3+x%5E%7B5%7D+%5Cright%29%5E2%7D&bg=ffffff&fg=5e5e5e&s=0&c=20201002)
Finalmente, simplificamos para obtener el siguiente el resultado
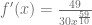
es creciente si esta se hace más grande a medida que crece la variable
. Formalmente, diremos que una función es creciente en un intervalo
si para todo
tal que
entonces
.
está a la izquierda de
, entonces
está por debajo de
pero además, podemos notar que la recta tangente a la curva en cualquier punto de este intervalo tendrá pendiente positiva
, esta será positiva.
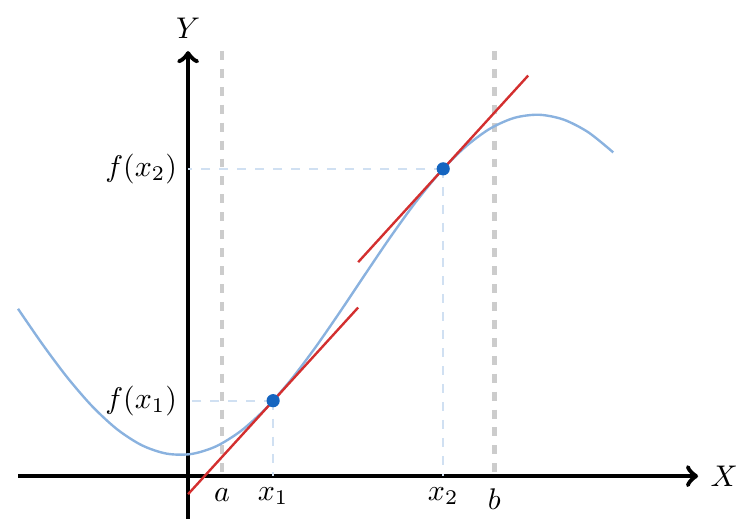
es decreciente si esta se hace más pequeña a medida que crece la variable
. Formalmente, diremos que una función es decreciente en un intervalo
si para todo
tal que
entonces
.
está a la izquierda de
, entonces
está por encima de
pero además, podemos notar que la recta tangente a la curva en cualquier punto de este intervalo tendrá pendiente negativa
, esta será negativa.
una función definida en un intervalo
, tenemos que para todo
, entonces
es creciente
, entonces
es decreciente
en todo su dominio, es decir, en el intervalo
.
y obtener que
. Notamos inmediatamente que
es un número positivo y la expresión
siempre es un número positivo, por lo tanto,
para todo número real
. Entonces, tomando en cuenta el criterio de la primera derivada, concluimos que la función es creciente en todo su dominio.
en el intervalo
.
y obtener que
. Notamos inmediatamente que
es un número positivo y la expresión
siempre es un número positivo, por lo tanto,
para todo número real
. Entonces, tomando en cuenta el criterio de la primera derivada, concluimos que la función es decreciente en el intervalo
, e incluso podemos afirmar que es decreciente en todo su dominio.
en el intervalo
.
y obtener que
. Notamos inmediatamente que
es un número positivo y la expresión
siempre es un número positivo, por lo tanto,
para todo número real
. Entonces, tomando en cuenta el criterio de la primera derivada, concluimos que la función es creciente en el intervalo
, e incluso podemos afirmar que es creciente en todo su dominio.
en su todo dominio, es decir, en el intervalo
.
y obtener que
. Nos preguntamos, ¿esta expresión es positiva o es negativa? La respuesta depende del valor de
, es por esto que tenemos que segmentar nuestra respuesta.
si
, entonces
es decreciente si
.
si
, entonces
es creciente si
.


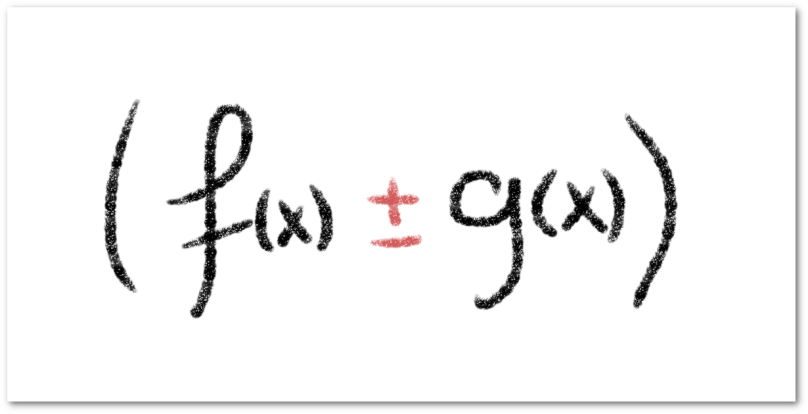





Debe estar conectado para enviar un comentario.