- Ecuaciones Diferenciales con Problemas de valor inicial
- Ecuaciones diferenciales con Problemas de condiciones en la frontera
- Ecuaciones Diferenciales con Problemas de valor inicial
- Ecuaciones diferenciales con Problemas de condiciones en la frontera
Hasta ahora hemos calculado la solución de algunas ecuaciones diferenciales de primer orden, es decir, de aquellas ecuaciones diferenciales en las que el mayor orden de las derivadas involucradas es igual a uno. Durante esta sección, estudiaremos ecuaciones diferenciales de orden mayor que uno, precisamente, ecuaciones diferenciales ordinarias de orden , es decir, aquellas definidas de la siguiente forma
También pudiera interesarte
Los métodos que se presentarán en esta sección se usarán para calcular la solución de las ecuaciones diferenciales ordinarias lineales de orden superior, es decir, aquellas expresadas como una combinación lineal (recordando que la linealidad es respecto a la variable y sus derivadas) de la siguiente forma
Donde y
son funciones que no necesariamente son lineales. Veamos algunos ejemplos para aprender a identificar este tipo de ecuaciones diferenciales.
Ejemplos
Ejemplo 1
La ecuación diferencial es lineal respecto
y
pues estos elementos permanecen inalterados, además, la derivada de mayor orden involucrada es de segundo orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria lineal de segundo orden.
Ejemplo 2
La ecuación diferencial es lineal respecto a la variable
y
pues estos elementos permanecen inalterados, además, la derivada de mayor orden involucrada es de tercer orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria lineal de tercer orden.
Ejemplo 3
La ecuación diferencial es lineal respecto a
,
y
pues estos elementos permanecen inalterados, además, la derivada de mayor orden involucrada es de segundo orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria lineal de segundo orden.
Ejemplo 4
La ecuación diferencial no es lineal respecto a
pues este elemento tiene potencia igual a siete, además, la derivada de mayor orden involucrada es de cuarto orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria no lineal de cuarto orden.
Ejemplo 5
La ecuación diferencial no es lineal respecto a
y
pues estos elementos están siendo multiplicados entre sí, además, la derivada de mayor orden involucrada es de segundo orden, por lo tanto, concluimos que es una ecuación diferencial ordinaria no lineal de segundo orden.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ecuaciones Diferenciales con Problemas de valor inicial
Al considerar ecuaciones diferenciales ordinarias de primer orden definimos una condición inicial sobre la variable como
, sin embargo, debemos ser cuidadosos al definir condiciones iniciales sobre ecuaciones de orden superior, pues en el caso de una ecuación diferencial ordinaria de orden
, la condición inicial está definida sobre la variable
y sus primeras
derivadas de la siguiente forma
Antes de empezar a calcular la solución de las ecuaciones diferenciales ordinarias de orden es importarse preguntarse: ¿cómo sabemos que en efecto podemos encontrar la solución de una ecuación que cumpla con esa condición? A continuación veremos un teorema que nos permitirá determinar si una ecuación diferencial con un problema de valor inicial tiene solución.
Teorema (De existencia y unicidad)
Sean y
funciones continuas en un intervalo
con
para todo
. Si
es un punto de este intervalo, entonces existe una única solución
para la ecuación
con la siguiente condición inicial para la variable y sus primeras
derivadas
Consideremos algunos ejemplos para entender la forma que deben tener las ecuaciones diferenciales para que cumplan con las condiciones de este teorema.
Ejemplos
Ejemplo 6
Consideremos la siguiente ecuación diferencial ordinaria con su respectivo problema de valor inicial
Entonces, ,
,
, y
son sus coeficientes y cada uno de estos es una función continua en cualquier intervalo
que contenga a
.
Por lo tanto, existe una única solución para esta ecuación en cualquier intervalo
.
Ejemplo 7
Consideremos la siguiente ecuación diferencial ordinaria con su respectivo problema de valor inicial
Entonces, ,
,
,
y
son sus coeficientes y cada uno de estos es una función continua en cualquier intervalo
que contenga a
.
Por lo tanto, existe una única solución para esta ecuación en cualquier intervalo
.
Ejemplo 8
Consideremos la siguiente ecuación diferencial ordinaria con su respectivo problema de valor inicial
Entonces, ,
,
y
son sus coeficientes y cada uno de estos es una función continua en cualquier intervalo
de la forma
contenga a
.
Por lo tanto, existe una única solución para esta ecuación en cualquier intervalo
de la forma
contenga a
.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ecuaciones diferenciales con Problemas de condiciones en la frontera
Al considerar una ecuación diferencial ordinaria de orden , podemos definir un problema de valor inicial fijando condiciones sobre las funciones
que definen la solución de la ecuación sobre un único punto.
Sin embargo, puede ocurrir que al considerar las funciones , estas no estén todas condicionadas en un único valor inicial, sino en puntos diferentes valores
. A este tipo de problemas los llamamos problemas de condiciones en la frontera.
De forma general, las condiciones en la frontera para una ecuación diferencial ordinaria de orden están expresados de la siguiente forma:
Y aunque estas condiciones parecieran complicadas, a medida que vamos particularizando los casos, estas se simplifican. Consideremos entonces, algunos ejemplos para entender como están expresadas las condiciones en la frontera para casos particulares.
Ejemplos
Ejemplo 9
Considere la siguiente ecuación diferencial ordinaria lineal de segundo orden con su respectiva condición en la frontera
Las condiciones y
son llamadas condiciones de frontera y, si observamos el caso general para ecuaciones ordinarias de segundo orden, podemos identificar estas condiciones de la siguiente forma
Ejemplo 10
Considere la siguiente ecuación diferencial ordinaria no lineal de tercer orden con su respectiva condición en la frontera
Las condiciones y
son llamadas condiciones de frontera y, si observamos el caso general para ecuaciones ordinarias de segundo orden, podemos identificar estas condiciones de la siguiente forma
Ejemplo 11
Considere la siguiente ecuación diferencial ordinaria no lineal de tercer orden con su respectiva condición en la frontera
Las condiciones ,
,
son llamadas condiciones de frontera y, si observamos el caso general para ecuaciones ordinarias de segundo orden, podemos identificar estas condiciones de la siguiente forma
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
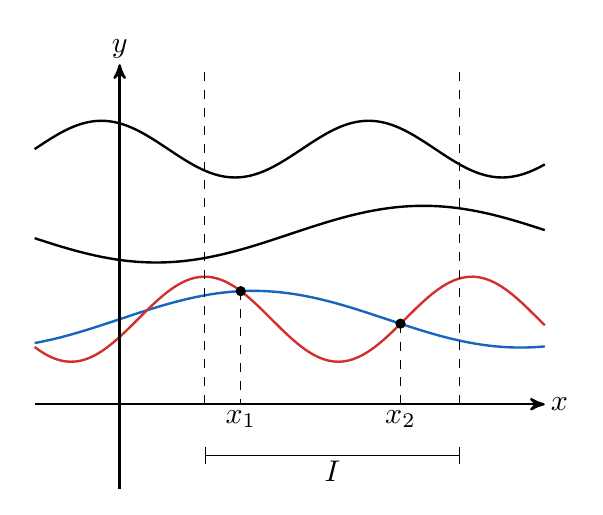
Es importante tomar en cuenta que los problemas de condiciones en la frontera pueden tener varias soluciones, una solución o ninguna solución. Esto se puede apreciar mejor con una interpretación gráfica de la solución de de una ecuación con problemas de condiciones en la frontera
Gráficamente, al considerar la solución de una ecuación diferencial ordinaria de orden , esta es una función que satisface igualdad planteada por la ecuación en un intervalo
que contiene a
, cuya gráfica pasa por los puntos
.
Para entender esta idea, en el siguiente gráfico se presenta la solución de una ecuación diferencial ordinaria de segundo orden. La solución es una función que satisface igualdad planteada por la ecuación en un intervalo que contiene a
y
; cuya gráfica (de la función solución) pasa por los puntos
y
.
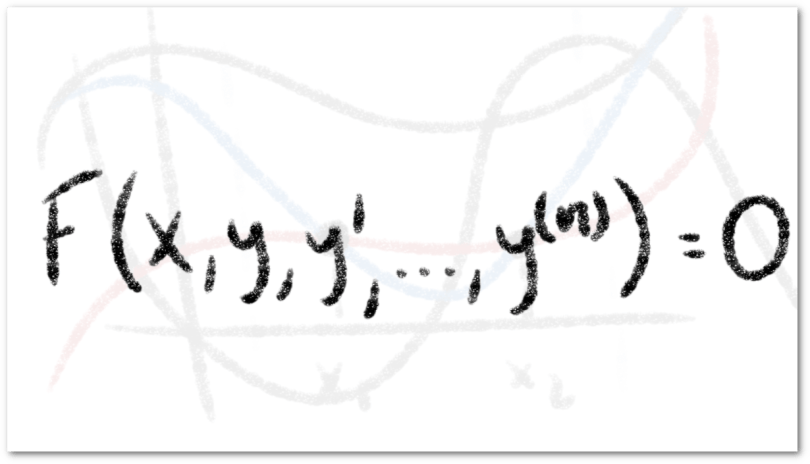


Debe estar conectado para enviar un comentario.