Derivadas Parciales de Orden Superior

Notación para Derivadas Parciales de Orden Superior
1. Ejemplos
  1. Ejemplo 1
  2. Ejemplo 2

También pudiera interesarte

Notación para Derivadas Parciales de Orden Superior

Podemos calcular derivadas parciales de orden superior teniendo en cuenta cual es la variable respecto a la cual estamos derivando. De esta forma, una vez que hemos calculado de la derivada de una función $f(x,y)$ respecto a la variable $x$ , es decir, $\frac{\partial f}{\partial x}$ ; podemos calcular la segunda derivada respecto a la variable $x$ y para esto usamos la siguiente notación:

$\displaystyle \dfrac{\partial \left( \frac{\partial f}{\partial x} \right)}{\partial x} = \dfrac{\partial^2 f}{\partial x^2}$

De igual forma, podemos calcular la segunda derivada respecto a la variable $y$ y usamos la siguiente notación:

$\displaystyle \dfrac{\partial \left( \frac{\partial f}{\partial x} \right)}{\partial y} = \dfrac{\partial^2 f}{\partial y \partial x}$

Una vez que hemos calculado de la derivada de una función $f(x,y)$ respecto a la variable $y$ , es decir, $\frac{\partial f}{\partial y}$ ; podemos calcular la segunda derivada respecto a la variable $x$ y para esto usamos la siguiente notación:

$\displaystyle \dfrac{\partial \left(\frac{\partial f}{\partial y} \right)}{\partial x} = \dfrac{\partial^2 f}{\partial x \partial y}$

De igual forma, podemos calcular la segunda derivada respecto a la varaible $y$ y usamos la siguiente notación:

$\displaystyle \dfrac{\partial \left(\frac{\partial f}{\partial y} \right)}{\partial y} = \dfrac{\partial^2 f}{\partial y^2}$

Cuando estamos aprendiendo a calcular derivadas parciales y más aún, de orden superior; es normal que uno se enrede con tantas variables. Con el diagrama que veremos a continuación se puede entender con un poco más de claridad que variables debemos considerar al derivar:

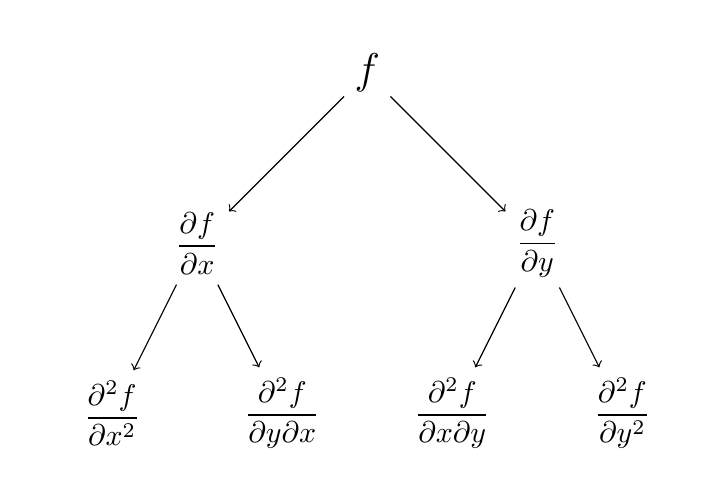
Diagrama Derivadas Parciales de Orden Superior | totumat.com

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Otra notación que puede ser útil para aligerar la escritura de las derivadas parciales consiste en escribir la función y usar un subíndice sobre esta para indicar cual es la variable respecto a la cual estamos derivando de la siguiente forma:

$f_x = \dfrac{\partial f}{\partial x}$

Podemos así, denotar las derivadas de orden superior como sigue:

$\dfrac{\partial^2 f}{\partial x^2} = (f_x)_x = f_{xx}$

$\dfrac{\partial^2 f}{\partial y \partial x} = (f_x)_y = f_{xy}$

$\dfrac{\partial^2 f}{\partial y^2} = (f_y)_y = f_{xx}$

$\dfrac{\partial^2 f}{\partial x \partial y} = (f_y)_x = f_{yx}$

En vista de esto, podemos replantear el diagrama visto anteriormente usando esta nueva notación:

Veamos con algunos ejemplos como calcular derivadas parciales de orden superior.

Ejemplos

Ejemplo 1

Sea $f(x,y)=2x^6+y^2 - 8$ una función definida en varias variables, calcule $\frac{\partial^2 f}{\partial x^2}$ .

Para calcular esta derivada, debemos calcular primero la derivada de $f$ respecto a la variable $x$ :

$\displaystyle \dfrac{\partial f}{\partial x} \; = \; \dfrac{\partial (2x^6+y^2 - 8)}{\partial x}$

$\displaystyle = \; \dfrac{\partial (2x^6)}{\partial x} + \dfrac{\partial (y^2)}{\partial x} - \dfrac{\partial (8)}{\partial x}$

$\displaystyle = \; 12x^5 + 0 - 0$

$\displaystyle = \; 12x^5$

Calculamos entonces la derivada de la función $\frac{\partial f}{\partial x}=2x^5$ respecto a la variable $x$ .

$\displaystyle \dfrac{\partial^2 f}{\partial x^2} \; = \; \dfrac{\partial (12x^5)}{\partial x} \; = \; 60x^4$

Supongamos que queremos calcular $\frac{\partial^2 f}{\partial y \partial x}$ , entonces debemos calcular la derivada de la función $\dfrac{\partial f}{\partial x}=2x^5$ respecto a la variable $y$ :

$\displaystyle \dfrac{\partial^2 f}{\partial y \partial x} \; = \; \dfrac{\partial (12x^5)}{\partial y} \; = \; 0$

Ejemplo 2

Sea $f(x,y)=5\sqrt{xy} - x^3y + 6x + 2$ una función definida en varias variables, calcule $\frac{\partial^2 f}{\partial y^2}$ .

Para calcular esta derivada, debemos calcular primero la derivada de $f$ respecto a la variable $y$ :

$\displaystyle \dfrac{\partial f}{\partial y} \; = \; \dfrac{\partial (5\sqrt{xy} - x^3y + 6x + 2)}{\partial y}$

$\displaystyle = \; \dfrac{\partial (5\sqrt{xy})}{\partial y} - \dfrac{\partial (x^3y)}{\partial y} + \dfrac{\partial (6x)}{\partial y} + \dfrac{\partial (2)}{\partial y}$

$\displaystyle = \; 5\dfrac{1}{2\sqrt{xy}} \cdot x - x^3 + 0 + 0$

$\displaystyle = \; \dfrac{5}{2}\dfrac{\sqrt{x}}{\sqrt{y}} - x^3$

Este último paso se debe a que $\frac{1}{\sqrt{xy}} \cdot x = \frac{x}{\sqrt{x}\sqrt{y}} = \frac{x}{\sqrt{x}}\frac{1}{\sqrt{y}} = \sqrt{x}\frac{1}{\sqrt{y}} = \frac{\sqrt{x}}{\sqrt{y}}$

Calculamos entonces la derivada de la función $\dfrac{\partial f}{\partial y} \; = \; \frac{5}{2}\frac{\sqrt{x}}{\sqrt{y}} - x^3$ respecto a la variable $y$ .

$\displaystyle \dfrac{\partial^2 f}{\partial y^2} \; = \; \dfrac{\partial \left( \frac{5}{2}\frac{\sqrt{x}}{\sqrt{y}} - x^3 \right) }{\partial y}$

$\displaystyle = \; \dfrac{\partial \left( \frac{5}{2}\frac{\sqrt{x}}{\sqrt{y}} \right) }{\partial y} - \dfrac{\partial (x^3)}{\partial y}$ *

$\displaystyle = \; \dfrac{5}{2}\sqrt{x} \left( \dfrac{-1}{2\sqrt{y^3}} \right) - 0$

$\displaystyle = \; -\dfrac{5\sqrt{x}}{4\sqrt{y^3}}$

*Note que al $x$ comportarse como una constante, es conveniente separarla de la variable $y$ , ya que de este modo es más fácil de derivar el producto.

Supongamos que queremos calcular $\frac{\partial^2 f}{\partial x \partial y}$ , entonces debemos calcular la derivada de la función $\frac{\partial f}{\partial y} = \frac{5}{2}\frac{\sqrt{x}}{\sqrt{y}} - x^3$ respecto a la variable $x$ :

$\displaystyle \dfrac{\partial^2 f}{\partial x \partial y} \; = \; \dfrac{\partial \left( \frac{5}{2}\frac{\sqrt{x}}{\sqrt{y}} - x^3 \right) }{\partial x}$

$\displaystyle = \; \dfrac{\partial \left( \frac{5}{2}\frac{\sqrt{x}}{\sqrt{y}} \right) }{\partial x} - \dfrac{\partial (x^3)}{\partial x}$

$\displaystyle = \; \frac{5}{2 \sqrt{y}} \dfrac{1}{2\sqrt{x}} - 3x^2$

$\displaystyle = \; \frac{5}{4 \sqrt{y} \sqrt{x}} - 3x^2$

$\displaystyle = \; \frac{5}{4 \sqrt{xy}} - 3x^2$