Funciones en Varias Variables

Es posible hacer un análisis marginal de este tipo de funciones usando derivadas pero estas funciones definen superficies en el espacio, así que en un punto de ellas existen infinitas rectas tangentes. Entonces, ¿cuál de todas las rectas tangentes será la que define la derivada?

También pudiera interesarte

Interpretación gráfica de la Derivada Parcial

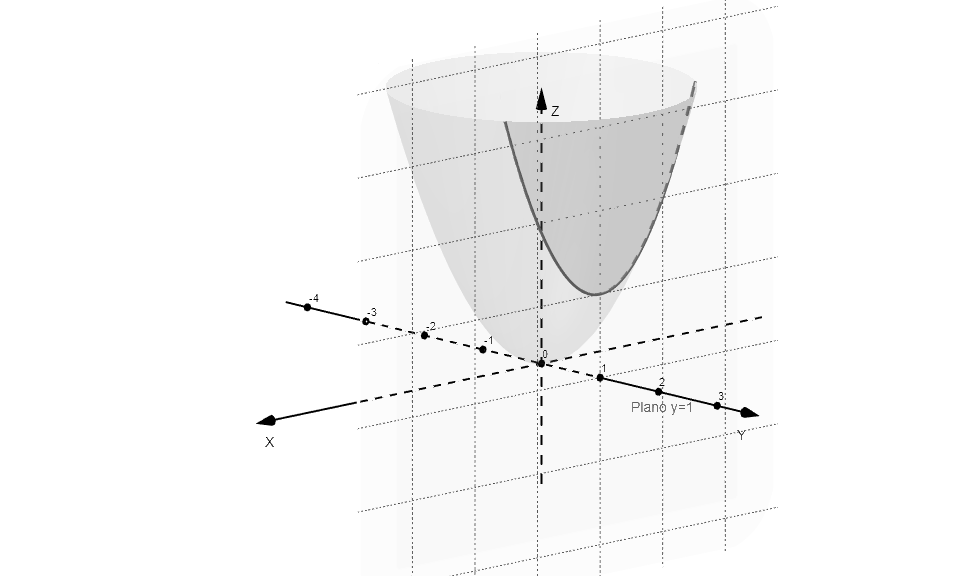
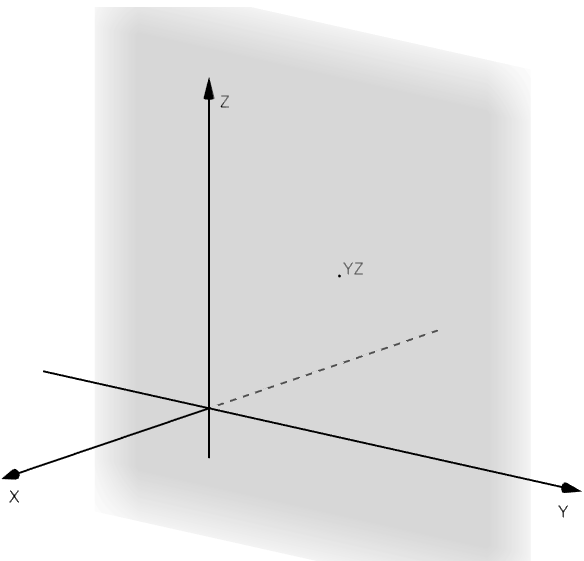
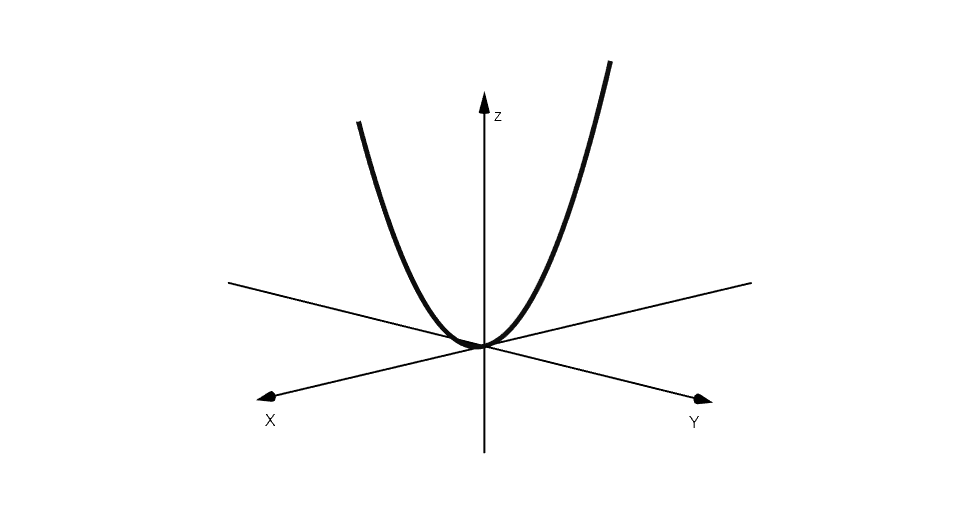
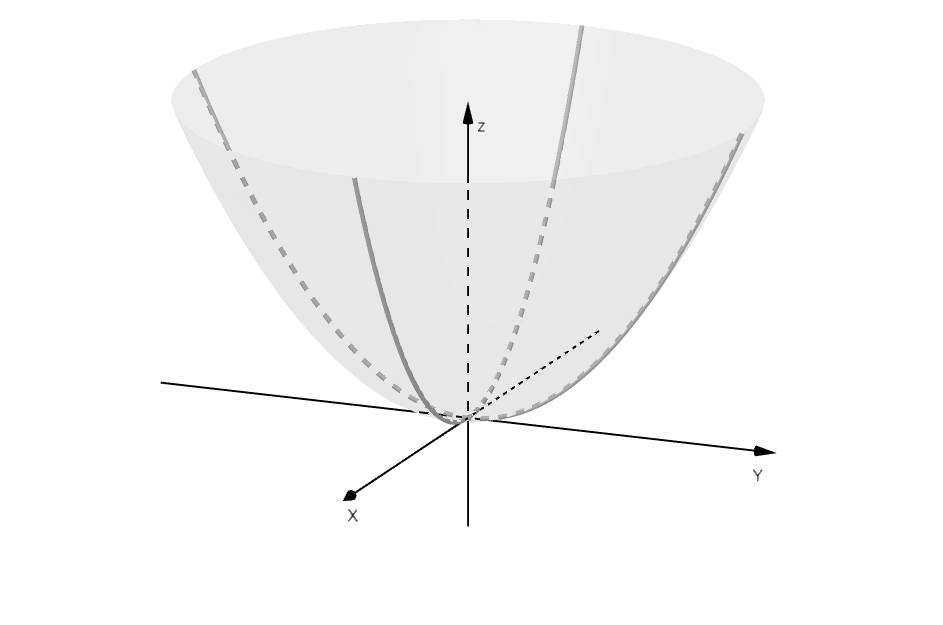
Para hacer un estudio marginal de una función definida en dos variables será necesario fijar una variable y variar la otra. Gráficamente lo que ocurre es al fijar una de las variables, estaremos cortando nuestra superficie con un plano y sobre este plano se proyectará una curva sobre la cual sí podremos hacer un estudio tal como lo hemos hecho antes.

Para entender lo que ocurre veamos un caso particular, consideremos la función $f(x,y)=x^2+y^2$ . Si fijamos la variable $y$ , digamos que $y=1$ , entonces la función se expresará de la forma

$f(x,1) = f(x) = x^2 + 1$

Notando que depende de sólo una variable, esta función estará definida en un plano paralelo al plano $XZ$ que pasa por el punto $(0,1,0)$ y corta a la superficie que define $f(xy)$ como se ve a continuación:

Notación de la Derivada Parcial

Tomando en cuenta esto, definimos de forma general la Derivada Parcial de una función $f(x,y)$ respecto a la variable $x$ como la derivada de la función $f(x,y)$ una vez que se ha fijado la variable $y$ y la denotamos con

$\displaystyle \frac{\partial f}{\partial x}$

De igual forma, definimos de forma general la derivada parcial de una función $f(x,y)$ respecto a la variable $y$ como la derivada de la función $f(x,y)$ una vez que se ha fijado la variable $x$ y la denotamos con

$\displaystyle \frac{\partial f}{\partial y}$

Definiendo las derivadas parciales de esta forma, podemos usar todas las reglas de derivación que se han establecido para el cálculo de derivadas de funciones de una variable. Veamos con algunos ejemplos como calcular este tipo de derivadas.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ejemplos

Ejemplo 1

Sea $f(x,y)=x^2+y^2$ una función definida en varias variables, calcule la derivada parcial respecto la variable $x$ , es decir, $\frac{\partial f}{\partial x}$ .

Primero debemos tomar en cuenta que si estamos derivando respecto a $x$ , entonces estamos variando a la variable $x$ y fijando la variable $y$ , por lo tanto la variable $y$ se comportará como una constante. Así,

$\displaystyle \frac{\partial f}{\partial x} \; = \; \frac{\partial (x^2 + y^2)}{\partial x}$

$\displaystyle = \; \frac{\partial (x^2)}{\partial x} + \frac{\partial (y^2)}{\partial x}$

$\displaystyle = \; 2x + 0$

$\displaystyle = \; 2x$

Si queremos calcular la derivada parcial respecto la variable $y$ , es decir, $\frac{\partial f}{\partial y}$ . Debemos notar que en este caso es la variable $x$ la que estamos fijando y en consecuencia será ésta la que se comporte como una constante.

$\displaystyle \frac{\partial f}{\partial y} \; = \; \frac{\partial (x^2 + y^2)}{\partial y}$

$\displaystyle \; = \; \frac{\partial (x^2)}{\partial y} + \frac{\partial (y^2)}{\partial y}$

$\displaystyle = \; 0 + 2y$

$\displaystyle = \; 2y$

Ejemplo 2

Sea $f(x,y)= 5x^8-2y^4 + 6xy$ . Calcule $\dfrac{\partial f}{\partial x}$ y $\dfrac{\partial f}{\partial y}$ .

Si queremos calcular la derivada parcial respecto la variable $x$ , entonces estamos variando a la variable $x$ y fijando la variable $y$ , por lo tanto la variable $y$ se comportará como una constante. Así,

$\displaystyle \frac{\partial f}{\partial x} \; = \; \frac{\partial (5x^8-2y^4 + 6xy)}{\partial x}$

$\displaystyle = \; \frac{\partial (5x^8)}{\partial x} - \frac{\partial (2y^4)}{\partial x} + \frac{\partial (6xy)}{\partial x}$

$\displaystyle = \; 40x^7 - 0 + 6y$

$\displaystyle = \; 40x^7 + 6y$

Recordemos que la derivada de $k\cdot x$ es igual a $k$ , donde $k$ es una constante. De esta forma, al comportarse la variable $y$ como una constante, entonces la derivada del producto $6xy$ será $6y$ .

Por otra parte, si queremos calcular la derivada parcial respecto la variable $y$ , entonces estamos variando a la variable $y$ y fijando la variable $x$ , por lo tanto la variable $x$ se comportará como una constante. Así,

$\displaystyle \frac{\partial f}{\partial y} \; = \; \frac{\partial (5x^8-2y^4 + 6xy)}{\partial y}$

$\displaystyle = \; \frac{\partial (5x^8)}{\partial y} - \frac{\partial (2y^4)}{\partial y} + \frac{\partial (6xy)}{\partial y}$

$\displaystyle = \; 0 - 8y^3 + 6x$

$\displaystyle = \; - 8y^3 + 6x$

En este caso $x$ se comporta como una constante, entonces la derivada del producto $6xy$ será $6x$ .

Ejemplo 3

Sea $f(x,y)= \ln(5x+7y) + 10x^3y^5$ . Calcule $\frac{\partial f}{\partial x}$ y $\frac{\partial f}{\partial y}$ .

$\displaystyle \frac{\partial f}{\partial x} \; = \; \frac{\partial (\ln(5x+7y) + 10x^3y^5)}{\partial x}$

$\displaystyle = \; \frac{\partial (\ln(5x+7y))}{\partial x} + \frac{\partial (10x^3y^5)}{\partial x}$

$\displaystyle = \; \frac{1}{5x+7y} \cdot 5 + 30x^2y^5$

$\displaystyle = \; \frac{5}{5x+7y} + 30x^2y^5$

$\displaystyle \frac{\partial f}{\partial y} \; = \; \frac{\partial (\ln(5x+7y) + 10x^3y^5)}{\partial y}$

$\displaystyle = \; \frac{\partial (\ln(5x+7y))}{\partial y} + \frac{\partial (10x^3y^5)}{\partial y}$

$\displaystyle = \; \frac{1}{5x+7y} \cdot 7 + 50x^3y^4$

$\displaystyle = \; \frac{7}{5x+7y} + 50x^3y^4$

Hemos estudiado funciones que de forma explícita, dependen de sólo una variable y aunque también hemos estudiado funciones que definidas de forma implícita relacionan dos variables, no hemos estudiado formalmente funciones que dependan de dos o más variables.

También pudiera interesarte

El Espacio Cartesiano

Para ir más allá, recurrimos a una nueva variable $z$ que dependerá enteramente de las variables $x$ y $y$ . Notando que al definir una tercera variable, podemos hacer la representación gráfica de este tipo de funciones tomando en cuenta que hasta ahora hemos construido nuestros espacios intersectando ejes coordenados de forma perpendicular.

Esta vez no será diferente, así que considerando el plano cartesiano, intersectaremos a este en el origen con un eje perpendicular a los Ejes $Y$ y $X$ generando así el espacio cartesiano que consta de tres ejes coordenados $X$ , $Y$ y $Z$ :

Los planos en el espacio

En este espacio podemos identificar tres planos principales, que se definen de la siguiente manera: El plano $XY$ que contiene todos los puntos de la forma $(x,y,0)$ , el plano $XZ$ que contiene todos los puntos de la forma $(x,0,z)$ y el plano $YZ$ que contiene todos los puntos de la forma $(0,y,z)$ .

Funciones en el espacio

De esta forma, podemos generalizar la definición de función que hasta ahora conocemos. Formalmente, si $R$ una región en el plano $XY$ , entonces definimos una función $f : R \to \mathbb{R}$ como una regla de correspondencia que corresponde a cada par ordenado de la región $R$ con un único número real $z = f(x,y)$ .

A este tipo de funciones las llamaremos funciones de dos variables. Evaluamos este tipo de funciones sustituyendo los valores de $x$ y $y$ por sus valores correspondientes, y así, calculamos sus imágenes. Veamos algunos ejemplos para entender como calcular imágenes.

Ejemplos

Ejemplo 1

Evalúe la función $f(x,y) = x^2 + y^2$ en el punto $(3,-1)$ . Entonces sustituimos $x$ por $3$ y $y$ por $-1$ de la siguiente forma:

$f(3,-1) = (3)^2 + (-1)^2= 9 + 1= 10$

Ejemplo 2

Evalúe la función $f(x,y) = \sqrt{x+20} + \textit{\Large e}^{2x-8} + 20$ en el punto $(-13,4)$ . Entonces sustituimos $x$ por $-13$ y $y$ por $4$ de la siguiente forma:

$f(-13,4) = \sqrt{-13+20} + \textit{\Large e}^{2(4)-8} + 20 = \sqrt{9} + \textit{\Large e}^{0} + 20 = 3 + 1 + 20 = 24$

Ejemplo 3

Evalúe la función $f(x,y) = \frac{7}{x+y}$ en el punto $(18,10)$ . Entonces sustituimos $x$ por $18$ y $y$ por $10$ de la siguiente forma:

$f(18,10) = \frac{7}{18+10} = \frac{7}{28} = \frac{1}{4}$

Gráfica de funciones en el espacio

Existen diversas técnicas para graficar este tipo de funciones definidas en varias variables, una de ellas es proyectar las curvas que esta define en cada plano.

Por ejemplo, si consideramos nuevamente la función $f(x,y)=x^2+y^2$ , podemos ver su proyección en el plano $XZ$ considerando $y=0$ , de esta forma la función se puede escribir de la siguiente forma: