Así como hemos definido las ecuaciones cuadráticas mediante una igualdad, es posible definir las inecuaciones cuadráticas mediante una desigualdad. A continuación veremos el segundo caso, que es cuando la desigualdad involucrada en la inecuación es «menor que» o «menor o igual que».
Entonces, considerando tres números reales ,
y
, expresamos una inecuación cuadrática de la siguiente forma;
Tomando en cuenta que si conocemos las raíces del polinomio , éste se puede reescribir como el producto de dos factores y de esta forma, desarrollamos una técnica para calcular la solución de las inecuaciones cuadráticas partiendo de la Ley de los Signos para la Multiplicación y planteando la siguiente pregunta:
¿Cuándo el producto de dos números es negativo?
Sean y
dos números reales. Si consideremos el producto
, ¿cuándo este producto es negativo? Para responder a esta pregunta, nos fijamos en la ley de los signos, pues recordando que más por menos es menos y menos por más es menos, podemos concluir que las condiciones que deben cumplir
y
para que se satisfaga la desigualdad
, son las siguientes:
Es decir, los y
deben ser el primero positivo y el segundo negativo o el primero negativo y el segundo positivo.
Este caso también aplica cuando consideramos la desigualdad «menor o igual» (). Veamos entonces en los siguientes ejemplos cómo calcular la solución de este tipo de ecuaciones.
También pudiera interesarte
Ejemplos
Ejemplo 1, «menor que»
Calcule los valores de que satisfacen la siguiente desigualdad:
Esta es una inecuación cuadrática donde el polinomio cuadrático ya está factorizado. Considerando los dos factores y
, deben ser el primero positivo y el segundo negativo o el primero negativo y el segundo positivo, así
Notamos entonces, que quedan planteadas cuatro inecuaciones lineales de las cuales se puede despejar la variable x con facilidad, de la siguiente forma:
La solución general de la inecuación cuadrática viene dada por todos los números que satisfacen las ecuaciones la línea (1) junto con todos los números que satisfacen las ecuaciones la línea (2).
Analíticamente representaremos la solución como la unión de los dos conjuntos que generados al calcular la solución de cada línea. Veamos entonces cómo calcular la solución de ambas líneas:
Solución 1:
Considerando que la línea (1) representa a todos los números que son mayores que -4 y menores que 1 al mismo tiempo, entonces consideramos la intersección de los intervalos y
así
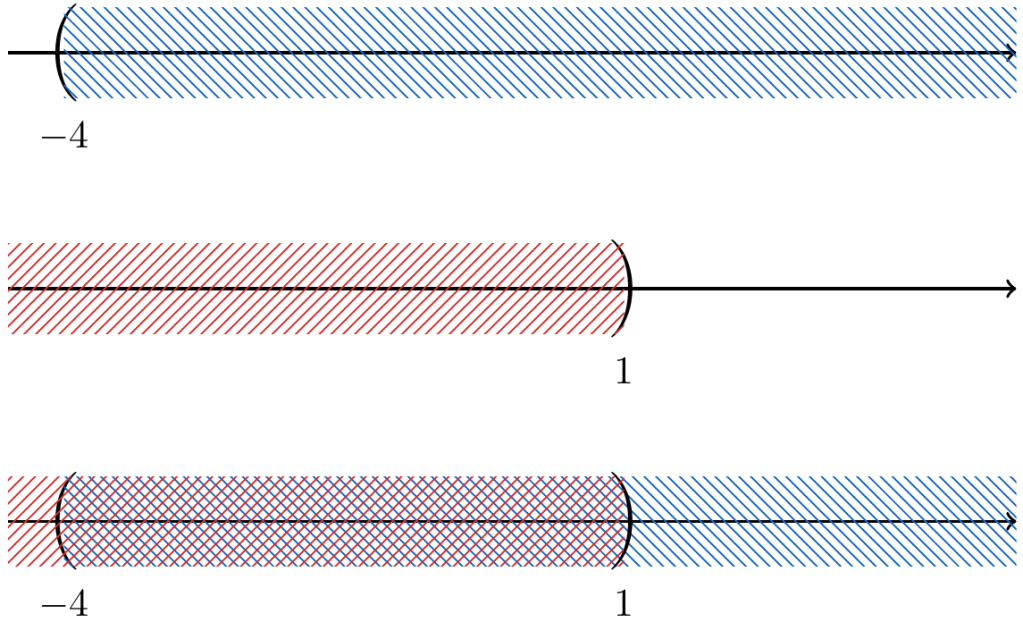
Solución 2:
Considerando que la línea (2) representa a todos los números que son menores que -4 y mayores que 1 al mismo tiempo, sin embargo, no existe ningún número que cumpla con esta condición. Entonces al considerar la intersección de los intervalos y
esta se representará con el conjunto vacío, así, tenemos que

Finalmente tomamos en cuenta que la solución general viene dada por todos los números que cumplen con la solución (1) o todos los elementos que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
Solución General:

Nota: el «ó» que se expresa en nuestra solución tiene un carácter lógico proposicional, esto quiere decir que es un «ó» inclusivo. Es decir, ambas opciones pueden presentar una solución para nuestra solución.
Imagínese que en una reunión con sus amigos, acuerdan llevar empanadas o pastelitos para comer, es decir, si alguien lleva una u otra cosa o ambas cosas, igual van a comer.
Consideremos ahora un ejemplo donde el polinomio cuadrático no está factorizado.
Ejemplo 2, «menor o igual que»
Calcule los valores de que satisfacen la siguiente desigualdad:
Notando que el polinomio no está factorizado, así que utilizamos el método del discriminante para factorizarlo. Entonces, considerando que sus coeficientes son ,
y
, planteamos la fórmula cuadrática de la siguiente forma:
Así, las raíces del polinomio cuadrático x^2 + x – \dfrac{3}{4} son y
, por lo tanto, podemos factorizarlo como
y en consecuencia, reescribimos la inecuación cuadrática original como sigue:
Al ser esta es una inecuación cuadrática donde el polinomio cuadrático ya está factorizado. Considerando los dos factores , deben ser el primero positivo y el segundo negativo o el primero negativo y el segundo positivo, así
Notamos entonces, que quedan planteadas cuatro inecuaciones lineales de las cuales se puede despejar la variable x con facilidad, de la siguiente forma:
La solución general de la inecuación cuadrática viene dada por todos los números que satisfacen las ecuaciones la línea (1) junto con todos los números que satisfacen las ecuaciones la línea (2).
Analíticamente representaremos la solución como la unión de los dos conjuntos que generados al calcular la solución de cada línea. Veamos entonces cómo calcular la solución de ambas líneas:
Solución 1:
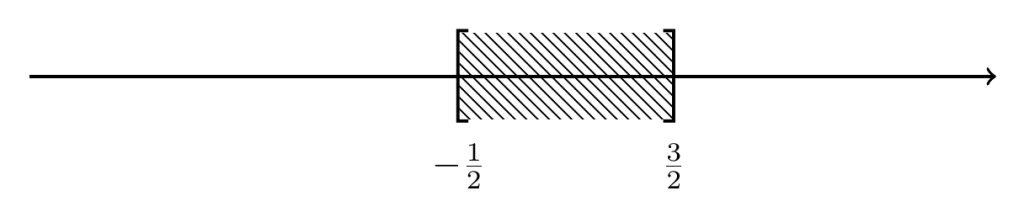
Considerando que la línea (1) representa a todos los números que son mayores que y menores que
al mismo tiempo, entonces consideramos la intersección de los intervalos
y
así

Solución 2:
Considerando que la línea (2) representa a todos los números que son menores que y mayores que
al mismo tiempo, sin embargo, no existe ningún número que cumpla con esta condición. Entonces al considerar la intersección de los intervalos
y
esta se representará con el conjunto vacío, así, tenemos que

Finalmente tomamos en cuenta que la solución general viene dada por todos los números que cumplen con la solución (1) o todos los elementos que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
Solución General: