- Límite infinito con variable finita
- Límite finito con variable infinita
- Límite infinito con variable infinita
¡Imagine el número más grande del mundo!
El estudio del comportamiento de una función puede involucrar valores muy grandes, tanto para la función como para la variable involucrada. A continuación veremos con detenimiento los distintos casos que se pueden presentar al estudiar el comportamiento de funciones que involucran valores muy grandes.
También pudiera interesarte
Límite infinito con variable finita
Consideremos la función , si consideramos valores de
menores que
, por ejemplo:
, su imagen será
;
, su imagen será
;
, su imagen será
; y así sucesivamente notamos que a medida que nos vamos acercando al cero, las imágenes crecen cada vez más. Entonces nos preguntamos siguiendo esta idea: ¿Hacia donde tiende
cuando
tiende a cero? La función alcanzará valores muy grandes que no pueden ser cuantificables, esta idea la denotamos con el infinito y la expresamos con el siguiente límite
Formalmente, diremos que una función tiende a más infinito cuando
tiende a
se expresa con el siguiente límite y posteriormente su interpretación matemática
Para todo número , existe un número
tal que
si entonces
Si consideramos ahora los valores de mayores que
, por ejemplo:
, su imagen será
;
, su imagen será
;
, su imagen será
; y así sucesivamente notamos que a medida que nos vamos acercando al cero, las imágenes decrecen cada vez más. La función alcanzará valores negativos muy grandes que no pueden ser cuantificables, esta idea la denotamos con el menos infinito y la expresamos con el siguiente límite
Formalmente, diremos que una función tiende a menos infinito cuando
tiende a
se expresa con el siguiente límite y posteriormente su interpretación matemática
Para todo número , existe un número
tal que
si entonces
De forma general, diremos que una función tiende a infinito cuando
tiende a
se expresa con el siguiente límite y posteriormente su interpretación matemática
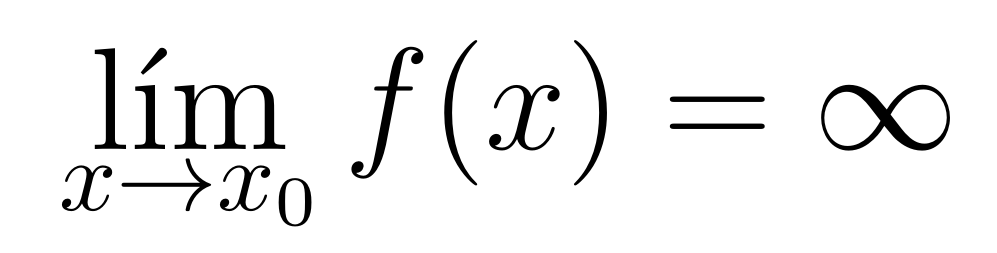
Para todo número , existe un número
tal que
si entonces
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Límite finito con variable infinita
Supongamos ahora que queremos estudiar el comportamiento de una función cuando la variable
adquiere valores muy altos. Supongamos que usted está en una fiesta de cumpleaños y que al final a usted le corresponde picar la torta (pastel): Si hay un sólo niño, le da toda la toda torta a ese niño; si hay dos niños, le da
de torta a cada niño; si hay tres niños, le da
de torta a cada niño; así sucesivamente. Notando que mientras más niños haya en la fiesta, más pequeño es el pedazo que le corresponde a cada uno, sin embargo, ningún niño se quedará sin torta.
Esta situación la podemos describir considerando la función , notando entonces que a medida que crece el valor de
, esta función decrece, es decir, la tendencia que tiene esta función es la de acercarse a cero. Tomando en cuenta que por más grande que sea el valor de
esta función nunca es igual a cero. Esta idea se expresa con el siguiente límite
Formalmente, diremos que una función tiende a un número real
cuando
tiende a infinito se expresa con el siguiente límite y posteriormente su interpretación matemática
Para todo número , existe un número
tal que
si entonces
Si consideramos nuevamente la función , también notamos que a medida que crece el valor de
pero hacia los números negativos, la tendencia que tiene esta función es la de acercarse a cero. Tomando en cuenta que por más grande que sea el valor de
esta función nunca es igual a cero. Esta idea se expresa con el siguiente límite
Formalmente, diremos que una función tiende a un número real
cuando
tiende a menos infinito se expresa con el siguiente límite y posteriormente su interpretación matemática
Para todo número , existe un número
tal que
si entonces
De forma general, diremos que una función tiende a un número real
cuando
tiende a infinito se expresa con el siguiente límite y posteriormente su interpretación matemática
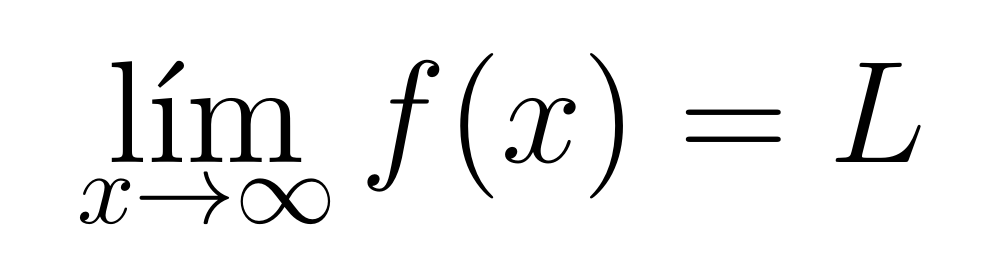
Para todo número , existe un número
tal que
si entonces
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Límite infinito con variable infinita
Consideremos la función identidad , esta función corresponde al 1 con el 1, al 2 con 2, al 3 con 3 y así sucesivamente identificará a cada número real con él mismo así que a medida que crece la variable
también crecerá la función. Particularmente, identificará un número muy grande con él mismo, Esta idea se expresa con el siguiente límite
Formalmente, diremos que una función tiende más infinito cuando
tiende a más infinito se expresa con el siguiente límite y posteriormente su interpretación matemática
Para todo número , existe un número
tal que
si entonces
Siguiendo esta idea, diremos que una función tiende menos infinito cuando
tiende a menos infinito se expresa con el siguiente límite y posteriormente su interpretación matemática
Para todo número , existe un número
tal que
si entonces
De forma general, diremos que una función tiende a infinito cuando
tiende a infinito se expresa con el siguiente límite y posteriormente su interpretación matemática
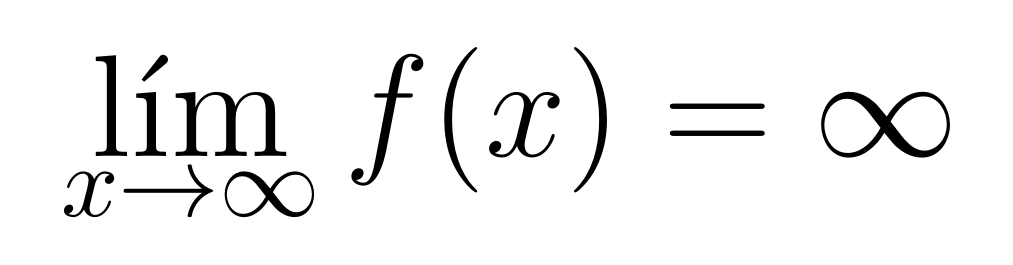
Para todo número , existe un número
tal que
si entonces


















Debe estar conectado para enviar un comentario.