Números Reales

03.11.201915.12.2022 Anthonny Arias-García5 comentarios

¿Qué es la raíz cuadrada de 2?

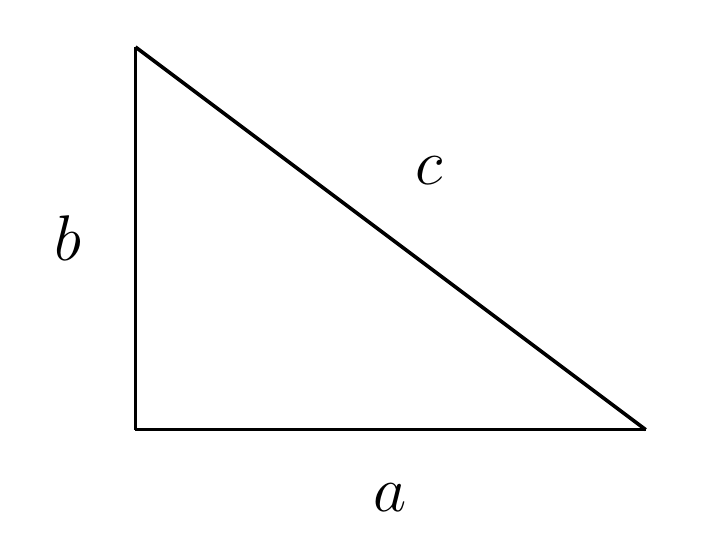
Empecemos considerando un triángulo rectángulo, es decir, un triángulo que tiene un ángulo recto (90°). Decimos que sus catetos son los lados adyacentes a este ángulo y la hipotenusa será el lado opuesto a dicho ángulo. Entonces, si un cateto mide $a$ , el otro cateto mide $b$ y la hipotenusa mide $c$ ; podemos dibujar un triángulo rectángulo de la siguiente forma:

Triángulo Rectángulo | totumat.com — Triángulo Rectángulo

También pudiera interesarte

El Teorema de Pitágoras establece que si usted tiene un triángulo rectángulo, el cuadrado de la hipotenusa será igual a la suma de los cuadrados de los catetos, es decir,

$c^2 = a^2 + b^2$

Con este resultado podemos decir que si tenemos un triángulo rectángulo cuyos catetos miden 3 y 4, entonces $3^2 + 4^2 = 9 + 16 = 25$ . Si la hipotenusa es c, tendremos que $c^2=25$ . Es decir, la hipotenusa será un número tal que multiplicado por él mismo nos da 25 como resultado, ya que $5^2=5\cdot 5 = 25$ , concluimos que la hipotenusa de este triángulo mide 5.

De igual forma si tenemos un triángulo rectángulo cuyos catetos miden 5 y 12, la hipotenusa medirá 13. Si los catetos miden 8 y 6, la hipotenusa medirá 10. Notemos que estos casos la medida de la hipotenusa es un número entero, sin embargo, este no es un caso general.

Supongamos que los catetos de un triángulo rectángulo miden 1 cada uno. Tendremos que $1^2 + 1^2 = 1+1=2$ . Entonces $c^2=2$ , ¿puede usted pensar en un número racional tal que al multiplicarlo por sí mismo nos dé 2 como resultado? ¿Será 1? ¿Será 2? ¿Qué tal 1,5? La respuesta es que no hay un número racional tal que multiplicado por sí mismo nos dé 2 como resultado.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Esta situación la solucionamos definiendo un nuevo número que no es natural, no es entero y tampoco es racional. Lo denotaremos con $\sqrt{2}$ y diremos que éste satisface la condición $c^2=2$ , es decir, $(\sqrt{2})^2=2$ .

$\sqrt{2}$

Hay una gran cantidad de situaciones en las que tendremos que definir nuevos números como $\sqrt{3}, \sqrt{5}, \sqrt{6}, \sqrt{13}, \sqrt{3453}, \sqrt{\frac{6}{19}}$ , etc. El símbolo $\sqrt{ \ \ }$ se llama raíz cuadrada, y así como se han presentado estos números, se presentarán otras ocasiones en los que debemos definir nuevos números como por ejemplo $\pi$ , $\phi$ ó $\epsilon$ .

Todos estos números a diferencia de los números racionales tendrán una extensión decimal infinita no periódica, es decir, su extensión decimal nunca se repite. Por ejemplo, con técnicas computarizadas se han logrado calcular hasta la fecha 31 4159 2653 5897 dígitos del número $\pi$ . Estos son los primeros 160 publicados en pi day:

3.1415 9265 3589 7932 3846 2643 3832 7950 2884 1971 6939 9375 1058 2097 4944 5923 0781 6406 2862 0899 862 8034 8253 4211 7067 98214 8086 5132 8230 6647 0938 4460 9550 5822 3172 5359 4081 2848 1117 45…

Definiremos un nuevo conjunto que alberga todos estos números y justamente por su característica de no ser racionales, lo llamaremos el conjunto de los Números Irracionales. Lo denotaremos con el símbolo $\mathbb{I}$ .

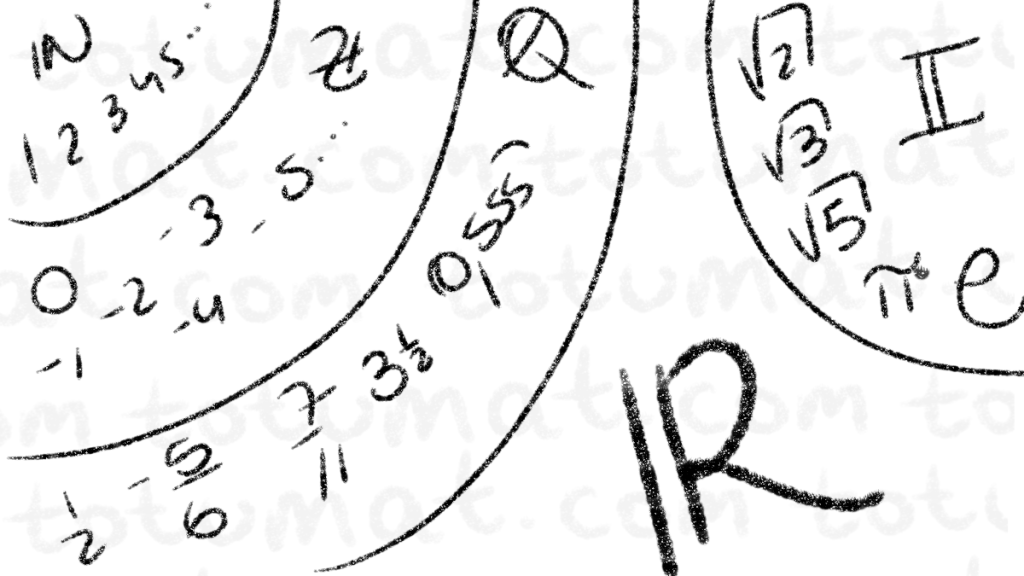
Considerando todos los conjuntos que hemos definido anteriormente, como los números naturales, enteros y racionales, definiremos un nuevo conjunto que alberga a todos los números racionales y todos los números irracionales, lo llamaremos el conjunto de los Números Reales y lo denotaremos por $\mathbb{R}$ , formalmente tendremos que

$\mathbb{R} = \mathbb{Q} \cup \mathbb{I}$

De esta forma nos podemos dar cuenta que el conjunto de los Números Racionales es un subconjunto del conjunto de los Números Reales, más aún, tendremos una cadena de contenciones de la siguiente forma:

$\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$

Es importante notar que a medida que definimos nuevos conjuntos, llenamos los «huecos» que hay entre los elementos de los conjuntos. Se asemeja a una historia de un autor anónimo que frecuentemente se encuentra en internet:

Anónimo…
Un profesor de filosofía llegó al salón de clases con su termo de café caliente como de costumbre, pero esta vez traía consigo una gran jarra y varios objetos. Sin mediar palabra el profesor llenó la jarra con pelotas de golf y preguntó a sus alumnos si la jarra estaba llena. Ellos asintieron con confusión por la obviedad de la pregunta.

Entonces el profesor tomó una caja de canicas y las vertió también dentro de la jarra; agitó con cuidado la jarra. Las canicas rodaron en las áreas abiertas que había entre las pelotas de golf. De nuevo les preguntó a sus estudiantes si la jarra estaba llena. Por segunda vez, todos estuvieron de acuerdo.

Después, el profesor tomó una caja de arena y la vertió en la jarra. Como ya podrán imaginarse, la arena se deslizó por todos los huecos que aún quedaban. El les preguntó una vez más si la jarra estaba llena. Los estudiantes respondieron al unísono «¡SÍII!».

Con mucha tranquilidad el profesor tomó su termo de café y lo vertió completamente en la jarra llenando efectivamente el espacio entre la arena. Los estudiantes rieron.

La historia generalmente viene acompañada con algunas frases de autoayuda o reflexiones sobre la vida pero eso no nos interesa, lo importante es notar que al representar el conjunto de los números reales de forma gráfica obtendremos una pasta cohesionada de números sin espacios entre ellos, que representaremos con una recta centrada en el cero de la siguiente forma:

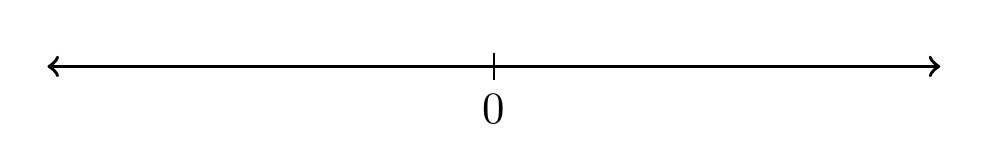
A esta recta la llamaremos Recta Real y en ella representaremos todos los números que hemos conocido hasta ahora.

– ¡Amor! 2 ha llegado de la guerra pero se ha vuelto irracional.
– ¡¿Qué?! ¡No 2! Él siempre ha sido… ¡Oh, dios!
– ¡Se ha radicalizado!

Conjuntos Numéricos: Naturales, Enteros, Racionales y Reales | totumat.com

Los números enteros y sus operaciones

31.10.201911.12.2022 Anthonny Arias-García2 comentarios

¿Qué son los números enteros?

Considere el número 4 y el número 7, estos dos son números naturales y por lo tanto ambos representan una cantidad de objetos. Suponga que se tiene una caja con 7 juguetes y se sacan 4 juguetes de ella. La caja quedaría con 3 juguetes. Ahora bien, ¿qué pasaría si se tiene una caja con 4 juguetes y queremos sacar 4 juguetes? ¿O si se quieren sacar 7 juguetes? ¿Puede el resultado de esta situación representarse con un número natural?

También pudiera interesarte

Respondamos la primera pregunta, si se tienen 4 juguetes en una caja y se sacan 4, no queda ningún juguete en la caja. Sin embargo, no conocemos ningún número natural que podamos corresponder con esta situación, así que definiremos un nuevo número llamado cero que denotaremos por $0$ y nos representará ninguna cantidad.

El número cero permite definir una nueva gama de números, de la siguiente forma: Si $a$ es un número natural entonces definimos un nuevo número $-a$ como su opuesto aditivo, que tendrá la siguiente propiedad:

$a + (-a) = (-a) + a = 0$

Nota: Podemos decir, además, que $a$ es el opuesto aditivo de $-a$ .

Sentando base en estos nuevos números podemos definir una nueva operación, si consideramos dos números naturales $a$ y $b$ , entonces al sumar $a$ con el opuesto aditivo de $b$ , la operación $a+(-b)$ se conoce como la resta y la escribimos de la siguiente forma:

$a-b$

Definiremos el conjunto de los Números Enteros como un nuevo conjunto que contiene a todos los números naturales junto con el número $0$ y el opuesto aditivo de cada número natural. Lo denotaremos por $\mathbb{Z}$ y lo expresamos extensivamente así:

$\mathbb{Z} = \{ \ldots,-3,-2,-1,0,1,2,3,\ldots \}$

Este conjunto continúa de manera indefinida siguiendo la secuencia de los números naturales $1,2,3,4, \ldots$ y además, siguiendo la secuencia de los opuestos aditivos de los números naturales $-1,-2,-3,-4, \ldots$ , es por eso que usamos tres puntos suspensivos al definirlo de forma extensiva.

También será posible representar este conjunto gráficamente, disponiendo cada elemento de forma ordenada en una recta. Los números naturales se escriben hacia la derecha y sus opuestos aditivos se escriben hacia la izquierda, el cero se escribe el medio de ambos, así

Representación gráfica de los números enteros | totumat.com

Es importante acotar que el conjunto de los números naturales es un subconjunto del conjunto de los números enteros, es decir,

$\mathbb{N} \subset \mathbb{Z}$

Operaciones entre Números Enteros

Al efectuar operaciones entre números naturales tales como la suma o el producto, es poco el cuidado que tenemos sobre el signo pues el resultado siempre es positivo. Sin embargo, la resta de números naturales puede presentar algunos problemas, es por esto que hemos definido los números enteros, así que veamos como se efectúan.

También pudiera interesarte

Suma y Resta de Números Enteros

Si consideramos los números enteros 2 y 3, entonces 3+2=5. Sin bien esta operación la podemos hacer en nuestra mente de forma inmediata, para entender de forma general la suma de dos números enteros consideremos la siguiente representación gráfica:

suma de números enteros tres más dos es igual a cinco | totumat.com — tres más dos es igual a cinco

Si sumamos 3+2, lo que en realidad estamos haciendo es trasladándonos dos espacios a la derecha del número 3 para caer en el número 5. Entonces, si así es la suma la pregunta natural que surge es: ¿cómo calculamos la resta?

Si sumamos 2+(-3)=2-3, estamos trasladándonos tres espacios a la izquierda del número 2 para caer en el -1. Consideremos la siguiente representación gráfica:

resta de números enteros dos menos tres es igual a menos uno | totumat.com — dos menos tres es igual a menos uno

De esta forma, podemos establecer una regla informal sobre la suma de números enteros de la siguiente forma:

Signos iguales se suman y se mantiene el signo.
Signos diferentes se restan y dejamos el signo del mayor.

Ejemplos

Ejemplo 1

Para efectuar la suma $7 +10$ , ambos números tienen signo positivo, así que los sumamos y mantenemos el signo positivo.

$7 +10 = 17$

Ejemplo 2

Para efectuar la suma $9 + (-3)$ , estos números tienen signos diferentes, así que los restamos y dejamos del signo del mayor, en este caso, $9$ es el mayor, así que dejamos el signo positivo.

$9 + (-3) = 9 - 3 = 6$

Ejemplo 3

Para efectuar la suma $(-20) + 11$ , estos números tienen signos diferentes, así que los restamos y dejamos del signo del mayor, en este caso, $20$ es el mayor, así que dejamos el signo negativo.

$(-20) + 11 = 11 - 20 = -9$

Ejemplo 4

Para efectuar la suma $(-37) + (-23)$ , ambos números tienen signo negativo, así que los sumamos y mantenemos el signo negativo.

$(-37) + (-23) = - 37 - 23 = - 60$

El producto de Enteros y la Ley de los Signos

El producto entre dos números enteros lo definiremos igual que el producto entre números naturales, pero debemos tener ciertas consideraciones sobre los signos. Sean a y b dos números naturales, entonces:

$(+a) \cdot (+b) = +(a \cdot b)$

$(-a) \cdot (+b) = -(a \cdot b)$

$(+a) \cdot (-b) = -(a \cdot b)$

$(-a) \cdot (-b) = +(a \cdot b)$

De esta forma, podemos establecer una regla informal conocida como la Ley de Los Signos sobre el producto de números enteros de la siguiente forma:

Más por más, más.
Más por menos, menos.
Menos por más, menos.
Menos por menos, más.

Ejemplo

Ejemplo 5

Para efectuar el producto $3 \cdot 3$ , el signo de ambos factores es positivo, así que los multiplicamos y el resultado tendrá signo positivo.

$3 \cdot 3 = 9$

Ejemplo 6

Para efectuar el producto $(-2) \cdot 5$ , el signo de ambos factores distinto, así que los multiplicamos y el resultado tendrá signo negativo.

$(-2) \cdot 5 = - ( 2 \cdot 5 ) = -10$

Ejemplo 7

Para efectuar el producto $6 \cdot (-3)$ , el signo de ambos factores distinto, así que los multiplicamos y el resultado tendrá signo negativo.

$6 \cdot (-3) = - (6 \cdot 3) = -18$

Ejemplo 8

Para efectuar el producto $(-4) \cdot (-8)$ , el signo de ambos factores es negativo, así que los multiplicamos y el resultado tendrá signo positivo.

$(-4) \cdot (-8) = (4 \cdot 8) = 32$

Definiendo los números enteros podemos encontrar una respuesta al problema que no se nos presentó cuando restábamos números naturales, pero aún nos queda una pregunta por responder sobre los números naturales y que se aplica también a los números enteros: ¿Qué sucede si dividimos dos números enteros? Debemos entonces definir los Números Racionales.

Operaciones entre conjuntos

28.10.201911.12.2022 Anthonny Arias-García2 comentarios

Al considerar dos conjuntos $A$ y $B$ , son diversas las operaciones que se pueden definir sobre ellos dos. Sin embargo, todas se basan en las operaciones de unión, intersección y el complemento. A continuación estudiaremos de forma concisa cada una de estas operaciones apoyándonos en Diagramas de Venn y usando conjuntos numéricos.

También pudiera interesarte

Unión de Conjuntos

Dados dos conjuntos $A$ y $B$ , definiremos la unión de estos dos conjuntos como un nuevo conjunto que contiene todos los elementos de $A$ junto con todos los elementos de $B$ y la denotaremos por $A \cup B$ . Si consideramos un elemento $c$ del conjunto $A \cup B$ entonces $c$ pertenece a $A$ o pertenece a $B$ .

Los Diagramas de Venn nos ayudan a expresar visualmente los conjuntos para entender algunas ideas, usualmente se usan círculos para representar conjuntos contenidos en un universo rectangular. A continuación, usaremos un Diagrama de Venn para expresar visualmente la unión entre dos conjuntos.