En el estudio de máximos y mínimos de funciones en varias variables, comúnmente se encuentran restricciones sobre las variables involucradas, por ejemplo, al considerar una función de costos conjuntos de una empresa que produce dos artículos A y B tal que la cantidad total de unidades producidas debe ser igual a 200, en este caso tendríamos que
suponiendo que es la cantidad de unidades producidas del artículo A y
la cantidad de unidades producidas del artículo B.
También pudiera interesarte
Método de los Multiplicadores de Lagrange
Al encontrar restricciones sobre las variables, debemos ser cautelosos en el cálculo de los extremos relativos ya que debemos tomar consideraciones adicionales. Debemos entonces establecer un nuevo método que nos permita calcular estos extremos relativos. De esta forma definimos el Método de los Multiplicadores de Lagrange de la siguiente forma:
Sea una función en varias variables y sea
una restricción sobre estas variables. Para calcular los puntos críticos de esta función. consideramos una variable auxiliar
y definimos una función auxiliar
como sigue
Nuestro propósito será el de calcular los puntos críticos de esta función auxiliar , pues si
es un punto crítico de
, entonces
es punto crítico de
sujeta a la restricción indicada. Para esto debemos calcular la solución del siguiente sistema de ecuaciones:
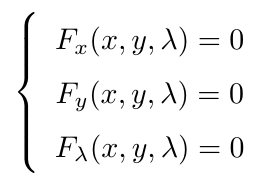
Finalmente, evaluamos la función en los puntos que satisfacen el sistema de ecuaciones y a partir de los valores resultantes concluimos lo siguiente:
- El mayor de estos valores será el máximo de la función
.
- El menor de estos valores será el mínimo de la función
.
- En el caso de haber sólo un valor, se utiliza el criterio de la Segunda Derivada para funciones de dos variables.
Veamos con algunos ejemplos como calcular los extremos relativos de funciones con restricción sobre sus variables.
Ejemplo
Sea una función, cuyas variables están restringidas a
. Determine los extremos relativos de esta función considerando la restricción indicada.
Para empezar, debemos reescribir la restricción como una función de la siguiente forma
Obteniendo la función , definimos nuestra función auxiliar
como
Y planteamos el sistema de ecuaciones siguiente para calcular los puntos críticos de esta función:

Sustituimos y
en la última ecuación para hallar el valor de
Ahora sustituimos en
y
:
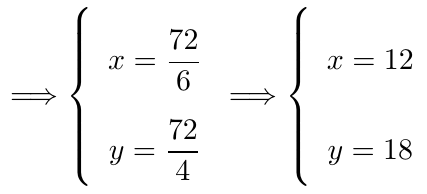
Concluimos entonces que el punto es el punto crítico de la función
y en consecuencia, el punto
es un punto crítico de la función
cuando las variables
y
están restringidas a
. Calculamos ahora las derivadas de orden superior de la función
para definir
.
Finalmente, como y
entonces por el criterio de la segunda derivada concluimos que la función
alcanza un mínimo relativo en el punto
.



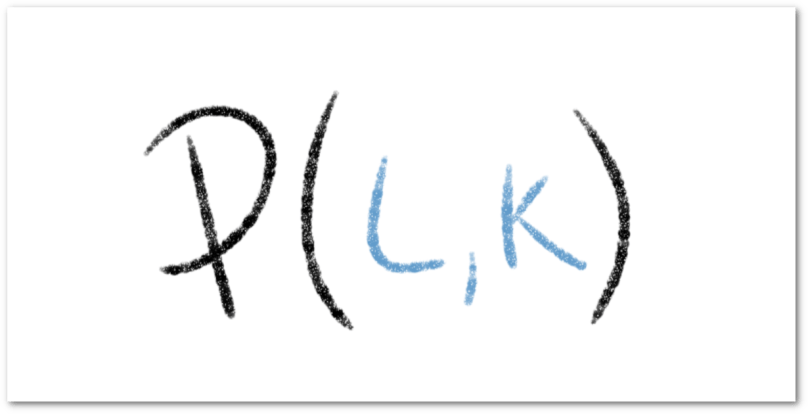



Debe estar conectado para enviar un comentario.