Calcular áreas puede resultar tedioso si cada vez debemos calcular límites de Sumas de Riemann, sin embargo, esto no necesariamente debe ser así. A continuación veremos un resultado matemático cuya importancia radica en que enlaza el cálculo diferencial (derivadas y antiderivadas) con un concepto netamente geométrico como el cálculo de áreas. Citando a Michael Spivak en su libro de Cálculo Infinitesimal:
La derivada no despliega toda su fuerza hasta que se alía con la «integral»… El estudio de las integrales requiere una preparación larga, pero una vez hecho este trabajo preliminar, las integrales constituyen un instrumento de valor incalculable para construir nuevas funciones y la derivada volverá a aparecer, más poderosa que nunca (en el Teorema Fundamental del Cálculo Infinitesimal)…
También pudiera interesarte
El Teorema Fundamental del Cálculo usualmente se presenta en dos partes: La primera parte nos permite definir un nuevo rango de funciones usando el concepto de antiderivada. La segunda parte es consecuencia de la primera y provee una herramienta vital para el cálculo de áreas bajo la curva.
El Teorema Fundamental del Cálculo, Parte I
Si es una función integrable en un intervalo
y
es una función definida como
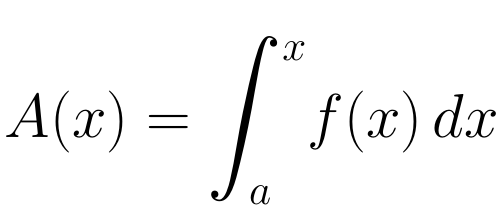
Si es continua en un punto
. Entonces, la función
es derivable en el punto
y además,
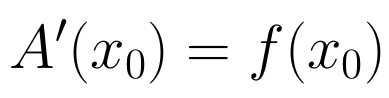
Demostración:
Consideremos un punto en el intervalo
, entonces verifiquemos si
es derivable en el punto
, es decir, verifiquemos que existe el siguiente límite:
Para esto, estudiemos las derivadas laterales de la función en el punto
para verificar si estas existen y son iguales.
Caso I: La derivada de la función por la derecha en el punto
está definida para
de la siguiente forma
La función es continua en el intervalo
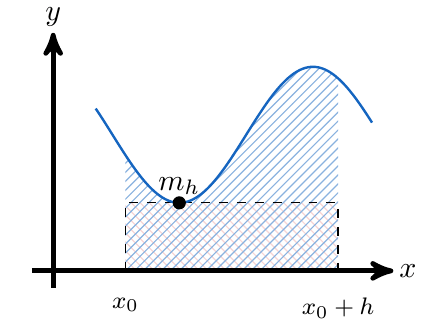
, esto quiere decir que es una función acotada, particularmente estará acotada inferiormente, esto quiere decir que del conjunto de todas las cotas inferiores, podemos considerar la más grande de ellas, es decir, podemos definir un número
de la siguiente forma:
E inmediatamente, podemos notar que el área del rectángulo con base y altura
, es menor que el área bajo la curva que define
.
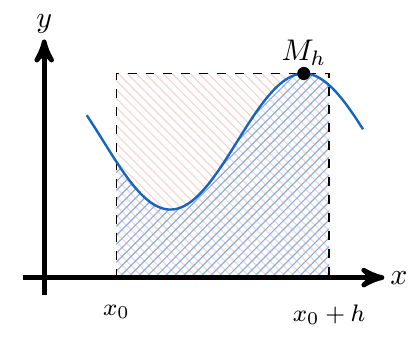
De igual forma, la función estará acotada superiormente, esto quiere decir que del conjunto de todas las cotas superiores, podemos considerar la más pequeña de ellas, es decir, podemos definir un número
de la siguiente forma:
E inmediatamente, podemos notar que el área del rectángulo con base y altura
, es mayor que el área bajo la curva que define
.
Tomando en cuenta los rectángulos señalados, podemos, decir que estas áreas acotan a la integral definida de la función en el intervalo
, es decir,
Tomando en cuenta que , podemos partir el área que bajo la curva que define
en el intervalo
de la siguiente forma:
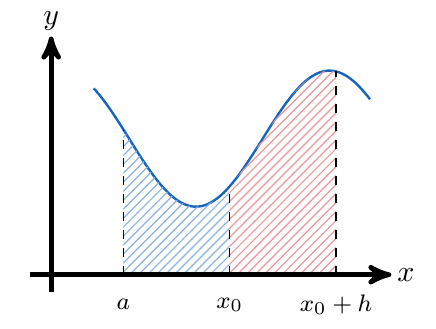
Es decir, un área en el intervalo y otra área en el intervalo
. De esta forma, podemos reescribir la integral sobre el intervalo
de la siguiente forma
A partir de esta igualdad, podemos hacer un simple despeje para concluir que
Inmediatamente, debemos notar que y que
para concluir que
y en consecuencia
Dividimos cada elemento de la inecuación por y como este es un valor positivo, las desigualdades permanecen inalteradas, así,
Finalmente, para determinar el límite de la función cuando
aplicamos el Teorema del Emparedado, pues notamos que ambas funciones
y
tienden a
cuando
. De esta forma, concluimos que
Caso II: La derivada de la función por la izquierda en el punto
está definida para
de la siguiente forma
La función es continua en el intervalo
, esto quiere decir que es una función acotada, particularmente estará acotada inferiormente, esto quiere decir que del conjunto de todas las cotas inferiores, podemos considerar la más grande de ellas, es decir, podemos definir un número
de la siguiente forma:
E inmediatamente, podemos notar que el área del rectángulo con base y altura
, es menor que el área bajo la curva que define
.
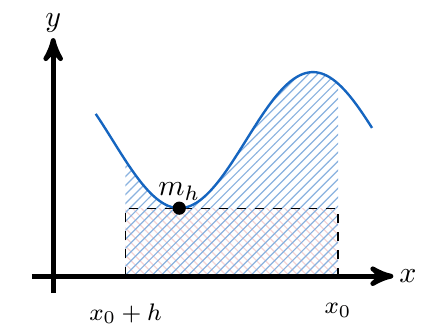
De igual forma, la función estará acotada superiormente, esto quiere decir que del conjunto de todas las cotas superiores, podemos considerar la más pequeña de ellas, es decir, podemos definir un número
de la siguiente forma:
E inmediatamente, podemos notar que el área del rectángulo con base y altura
, es mayor que el área bajo la curva que define
.

Tomando en cuenta los rectángulos señalados, podemos, decir que estas áreas acotan a la integral definida de la función en el intervalo
, es decir,
Tomando en cuenta que , podemos partir el área que bajo la curva que define
en el intervalo
de la siguiente forma:
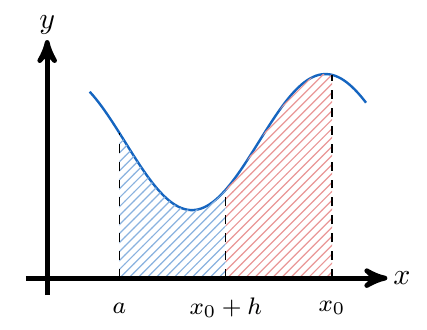
Es decir, un área en el intervalo y otra área en el intervalo
. De esta forma, podemos reescribir la integral sobre el intervalo
de la siguiente forma
A partir de esta igualdad, podemos hacer un simple despeje para concluir que
Inmediatamente, debemos notar que y que
para concluir que
y en consecuencia
Dividimos cada elemento de la inecuación por y como este es un valor positivo, las desigualdades permanecen inalteradas, así,
Finalmente, para determinar el límite de la función cuando
aplicamos el Teorema del Emparedado, pues notamos que ambas funciones
y
tienden a
cuando
. De esta forma, concluimos que
Habiendo calculado las derivadas laterales, verificando que estas existen y son iguales, concluimos que la derivada de la función en el punto
existe y está definida de la siguiente forma
Que es lo que queríamos demostrar.
Es importante destacar, que si la función en esta primera parte del Teorema Fundamental del Cálculo es continua en todo el intervalo
, entonces podemos concluir que para todo
, se tiene que
De esta forma, sentamos una base para poder enunciar la segunda parte del Teorema Fundamental del Cálculo.
El Teorema Fundamental del Cálculo, Parte II
Si es una función continua en un intervalo
y
es una antiderivada de esta, entonces
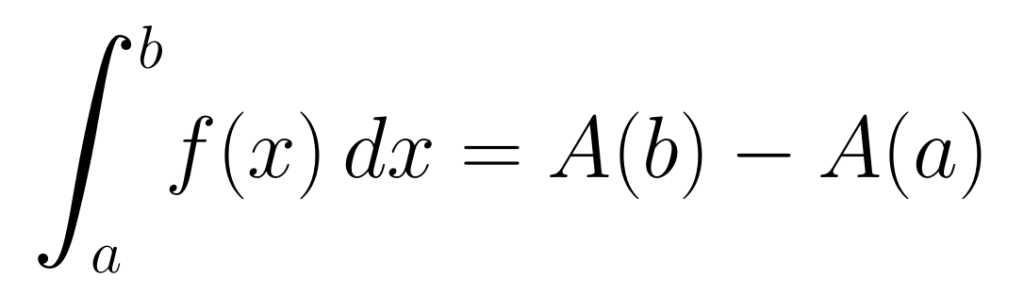
Cálculo de Área Bajo la Curva
Esta segunda parte es la que presentará particular interés para lo que queremos desarrollar, pues usando esta herramienta podemos calcular áreas bajo curvas sin tener que recurrir al cálculo tedioso de límites o de sumatorias. Veamos con algunos ejemplos como calcular áreas bajo curvas.
Ejemplos
Ejemplo 1
Calcule el área bajo la curva en el intervalo
.
Identificamos el área que queremos calcular
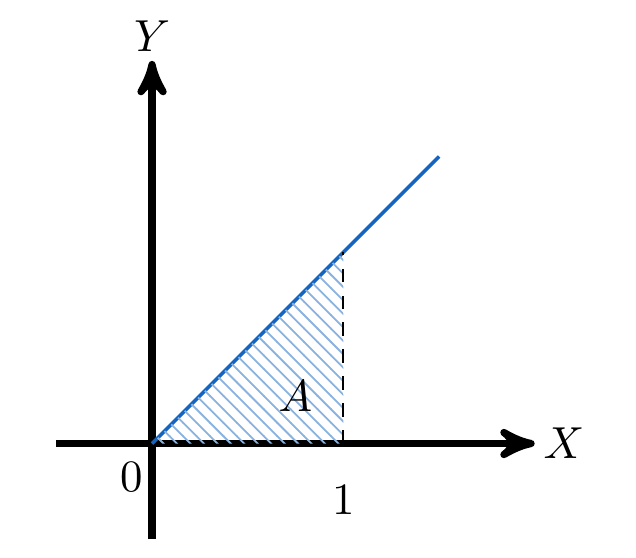
Calculamos el área usando el Teorema Fundamental del Cálculo, entonces
Ejemplo 2
Calcule el área bajo la curva en el intervalo
.
Identificamos el área que queremos calcular
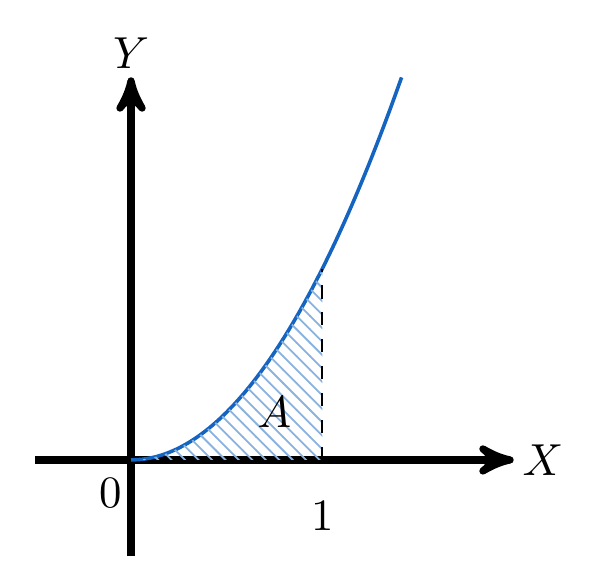
Calculamos el área usando el Teorema Fundamental del Cálculo, entonces
Ejemplo 3
Calcule el área bajo la curva en el intervalo
.
Identificamos el área que queremos calcular
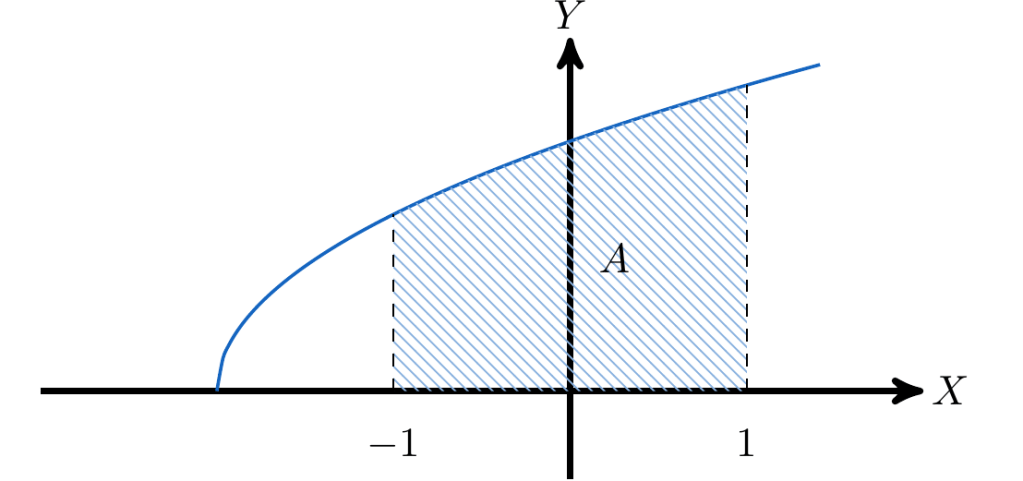
Calculamos el área usando el Teorema Fundamental del Cálculo, entonces
Es importante señalar que aunque la integral definida es una herramienta usada principalmente para calcular áreas bajo curvas, el Teorema Fundamental del Cálculo permite determinar elementos de interés en distintos campos de la ciencia, ingeniería y economía; es por esto que debemos tomar en cuenta que al considerar aplicaciones prácticas, estas pueden no representar áreas en el plano cartesiano.
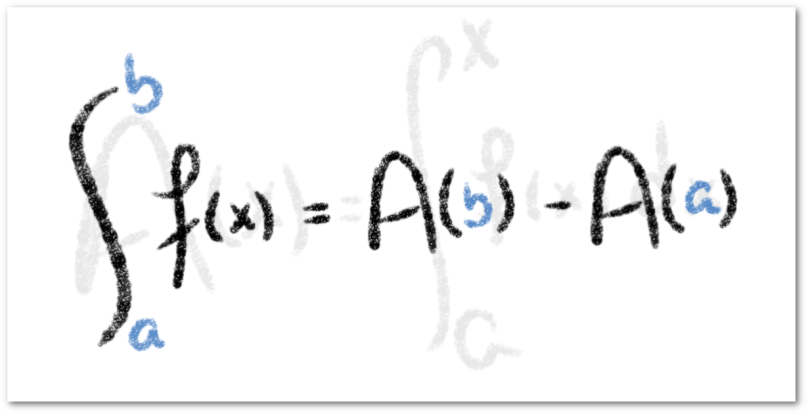





















Debe estar conectado para enviar un comentario.