Caso: «Mayor que»
Al definir el valor absoluto de un número real, hemos visto que es igual a la distancia entre dicho número y el número cero. Partiendo de esta definición, pudimos definir ecuaciones que involucran el valor absoluto de una variable.
De forma que si queremos determinar todos los números que cuya distancia entre cuya distancia a cero es igual a , entonces planteamos la siguiente ecuación:
y finalmente, determinamos que estos números son
y
.
Pero, ¿y si queremos determinar todos los números cuya distancia a cero es mayor que ? Para dar respuesta a esta pregunta, podemos plantear la siguiente inecuación:
También pudiera interesarte
Entonces, ¿qué números satisfacen dicha inecuación? Podemos tantear las respuestas, por ejemplo: el número no la satisface, pues
y
no es mayor que
. Así podemos probar con los números
,
y
pero ninguno de estos números satisface la inecuación.
Sin embargo, si consideramos ,
u
podemos ver que estos números sí satisfacen la inecuación y en general podemos decir que cualquier número mayor que
satisface la inecuación pero, ¿serán esos los únicos números que satisfacen la inecuación?
La respuesta es no, pues si consideramos ,
u
entonces estos números también satisfacen la inecuación y en general podemos decir que cualquier número menor que
satisface la inecuación.
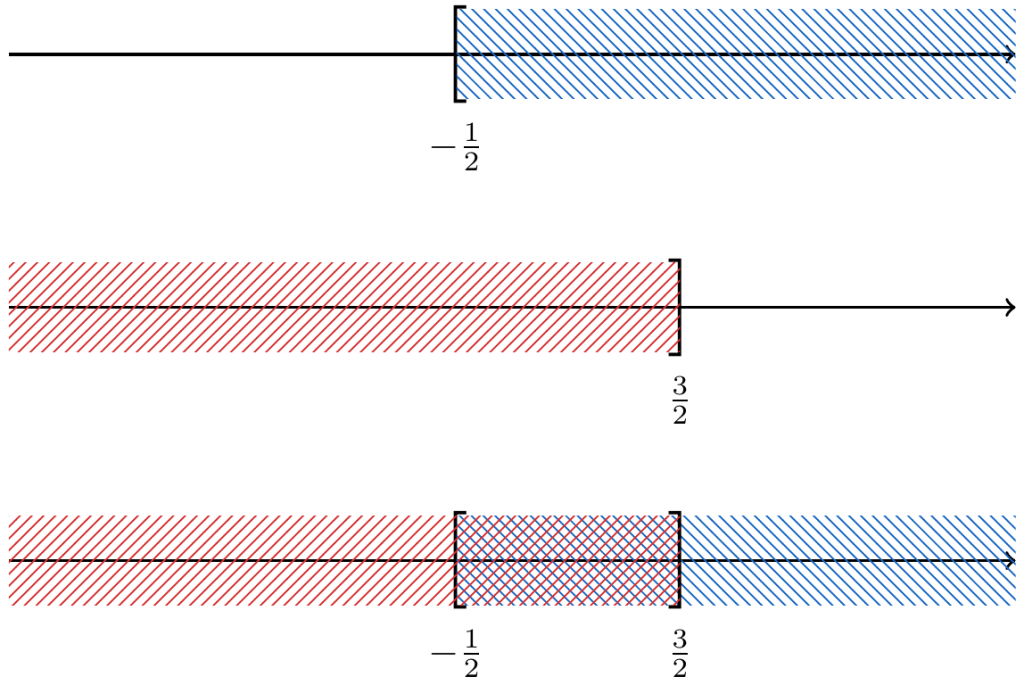
Razonando de esta forma, podemos concluir que cualquier número que sea mayor que o menor que
satisface la inecuación
. Gráficamente, podemos representar todos estos números en la recta real de la siguiente forma:

En general, diremos que al considerar una inecuación de la forma , donde
es un número real; la solución viene dada por todos los números mayores que
ó todos los números menores que
, formalmente se puede calcular la solución planteando la siguiente equivalencia:
Nota: el «ó» que se expresa en nuestra solución tiene un carácter lógico proposicional, esto quiere decir que es un «ó» inclusivo. Es decir, ambas opciones pueden presentar una solución para nuestra solución.
Imagínese que en una reunión con sus amigos, acuerdan llevar empanadas o pastelitos para comer, es decir, si sólo hay empanadas, solo hay pastelitos o hay ambas cosas, igual van a comer.
Veamos con algunos ejemplos como calcular la solución de este tipo de inecuaciones.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 1
Calcule los valores de que satisfacen la siguiente desigualdad
Para calcular la solución de esta ecuación, debemos plantear dos casos:
- Cuando la variable que está dentro del valor absoluto es mayor que la expresión que está en el lado derecho de la inecuación.
- Cuando la variable que está dentro del valor absoluto es menor que el opuesto aditivo de la expresión que está en el lado derecho de la inecuación.
De esta forma, planteamos dos ecuaciones:
Entonces, calculamos cada una de las ecuaciones planteadas:
Solución (1):
La solución de esta inecuación viene dada por todos los valores mayores que , formalmente,

Solución (2):
La solución de esta inecuación viene dada por todos los valores menores que , formalmente,

Finalmente tomamos en cuenta que la solución general viene dada por todos los números que cumplen con la solución (1) o todos los números que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
Solución General:

Ejemplo 2
Calcule los valores de que satisfacen la siguiente desigualdad
Para calcular la solución de esta ecuación, debemos plantear dos casos:
- Cuando la variable que está dentro del valor absoluto es mayor o igual que la expresión que está en el lado derecho de la inecuación.
- Cuando la variable que está dentro del valor absoluto es menor o igual que el opuesto aditivo de la expresión que está en el lado derecho de la inecuación.
De esta forma, planteamos dos ecuaciones:
Entonces, calculamos cada una de las ecuaciones planteadas:
Solución (1):
La solución de esta inecuación viene dada por todos los valores mayores o iguales que , formalmente,

Solución (2):
La solución de esta inecuación viene dada por todos los valores menores o iguales que , formalmente,
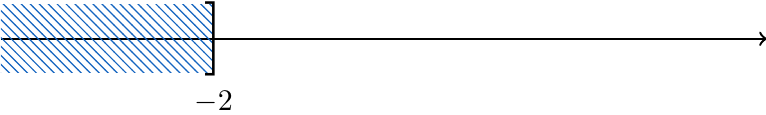
Finalmente tomamos en cuenta que la solución general viene dada por todos los números que cumplen con la solución (1) o todos los números que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
Solución General:
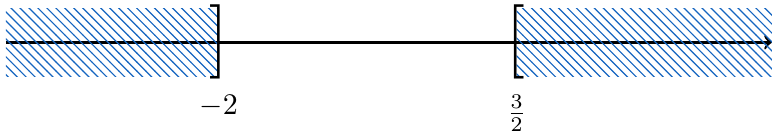
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 3: Valor absoluto mayor que un número negativo
Calcule los valores de que satisfacen la desigualdad
Al considerar esta inecuación, no es necesario hacer el procedimiento que hemos visto en los primeros ejemplos pues recordando que el valor absoluto de un número siempre es positivo, tenemos que sea cual sea el valor de x ese valor absoluto siempre será mayor que -8. Básicamente la pregunta es: ¿cuándo un número positivo es mayor que un número negativo?
La respuesta es: Siempre. Por lo tanto, la solución de esta inecuación viene dada por el conjunto de todos los números reales:
Ejemplo 4: Variables en ambos lados de la inecuación
Calcule los valores de que satisfacen la siguiente desigualdad
Lo primero que debemos notar al calcular la solución de esta inecuación, es que en ambos lados de la desigualdad hay una incógnita. Así que al final debemos tener evaluar para qué valores, esta desigualdad tiene sentido.
Para calcular la solución de esta ecuación, debemos plantear dos casos:
- Cuando la variable que está dentro del valor absoluto es mayor que la expresión que está en el lado derecho de la inecuación.
- Cuando la variable que está dentro del valor absoluto es menor que el opuesto aditivo de la expresión que está en el lado derecho de la inecuación.
De esta forma, planteamos dos ecuaciones:
Entonces, calculamos cada una de las ecuaciones planteadas:
Solución (1):
La solución de esta inecuación viene dada por todos los valores mayores que , formalmente,

Solución (2):
La solución de esta inecuación viene dada por todos los valores menores que , formalmente,

Definimos la solución parcial a partir de todos los números que cumplen con la solución (1) o todos los números que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
Solución Parcial:

Para determinar la solución general, debemos verificar los valores de para los cuales la expresión
es negativa, pues para estos valores, la desigualdad
siempre se cumple. Entonces, consideramos la siguiente condición sobre la variable

Finalmente, la solución general se define como la solución parcial incluyendo la condición, es decir,
Solución General:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 5: Variables en ambos lados de la inecuación
Calcule los valores de que satisfacen la siguiente desigualdad
Lo primero que debemos notar al calcular la solución de esta inecuación, es que en ambos lados de la desigualdad hay una incógnita. Así que al final debemos tener evaluar para qué valores, esta desigualdad tiene sentido.
Para calcular la solución de esta ecuación, debemos plantear dos casos:
- Cuando la variable que está dentro del valor absoluto es mayor o igual que la expresión que está en el lado derecho de la inecuación.
- Cuando la variable que está dentro del valor absoluto es menor o igual que el opuesto aditivo de la expresión que está en el lado derecho de la inecuación.
De esta forma, planteamos dos ecuaciones:
Entonces, calculamos cada una de las ecuaciones planteadas:
Solución (1):
La solución de esta inecuación viene dada por todos los valores menores o iguales que , formalmente,

Solución (2):
La solución de esta inecuación viene dada por todos los valores menores que , formalmente,

Definimos la solución parcial a partir de todos los números que cumplen con la solución (1) o todos los números que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
Solución Parcial:

Para determinar la solución general, debemos verificar los valores de para los cuales la expresión
es negativa, pues para estos valores, la desigualdad
siempre se cumple. Entonces, consideramos la siguiente condición sobre la variable

Finalmente, la solución general se define como la solución parcial incluyendo la condición, es decir,
Solución General:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 6: Se anula la variable en la inecuación
Calcule los valores de que satisfacen la siguiente desigualdad
Lo primero que debemos notar al calcular la solución de esta inecuación, es que en ambos lados de la desigualdad hay una incógnita. Así que al final debemos tener evaluar para qué valores, esta desigualdad tiene sentido.
Para calcular la solución de esta ecuación, debemos plantear dos casos:
- Cuando la variable que está dentro del valor absoluto es mayor o igual que la expresión que está en el lado derecho de la inecuación.
- Cuando la variable que está dentro del valor absoluto es menor o igual que el opuesto aditivo de la expresión que está en el lado derecho de la inecuación.
De esta forma, planteamos dos ecuaciones:
Entonces, calculamos cada una de las ecuaciones planteadas:
Solución (1):
Podemos notar que se anularon las variables y obtuvimos la desigualdad , esta desigualdad es falsa, por lo tanto, la solución aportada por esta inecuación se representa con el conjunto vacío
pues no hay ningún valor de
que la satisfaga.
Solución (2):
La solución de esta inecuación viene dada por todos los valores menores o iguales que , formalmente,

Definimos la solución parcial a partir de todos los números que cumplen con la solución (1) o todos los números que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
Solución Parcial:

Para determinar la solución general, debemos verificar los valores de para los cuales la expresión
es negativa, pues para estos valores, la desigualdad
siempre se cumple. Entonces, consideramos la siguiente condición sobre la variable

Finalmente, la solución general se define como la solución parcial incluyendo la condición, es decir,
Solución General:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 7: Se anula la variable en la inecuación
Calcule los valores de que satisfacen la siguiente desigualdad
Lo primero que debemos notar al calcular la solución de esta inecuación, es que en ambos lados de la desigualdad hay una incógnita. Así que al final debemos tener evaluar para qué valores, esta desigualdad tiene sentido.
Para calcular la solución de esta ecuación, debemos plantear dos casos:
- Cuando la variable que está dentro del valor absoluto es mayor o igual que la expresión que está en el lado derecho de la inecuación.
- Cuando la variable que está dentro del valor absoluto es menor o igual que el opuesto aditivo de la expresión que está en el lado derecho de la inecuación.
De esta forma, planteamos dos ecuaciones:
Entonces, calculamos cada una de las ecuaciones planteadas:
Solución (1):
Podemos notar que se anularon las variables y obtuvimos la desigualdad , esta desigualdad es verdadera, por lo tanto, la solución aportada por esta inecuación se representa con todo el conjunto los números reales
pues cualquier valor de
que la satisface.

Solución (2):
La solución de esta inecuación viene dada por todos los valores menores que , formalmente,

Definimos la solución parcial a partir de todos los números que cumplen con la solución (1) o todos los números que cumplen con la solución (2). Por lo tanto, consideraremos la unión de la solución (1) y (2).
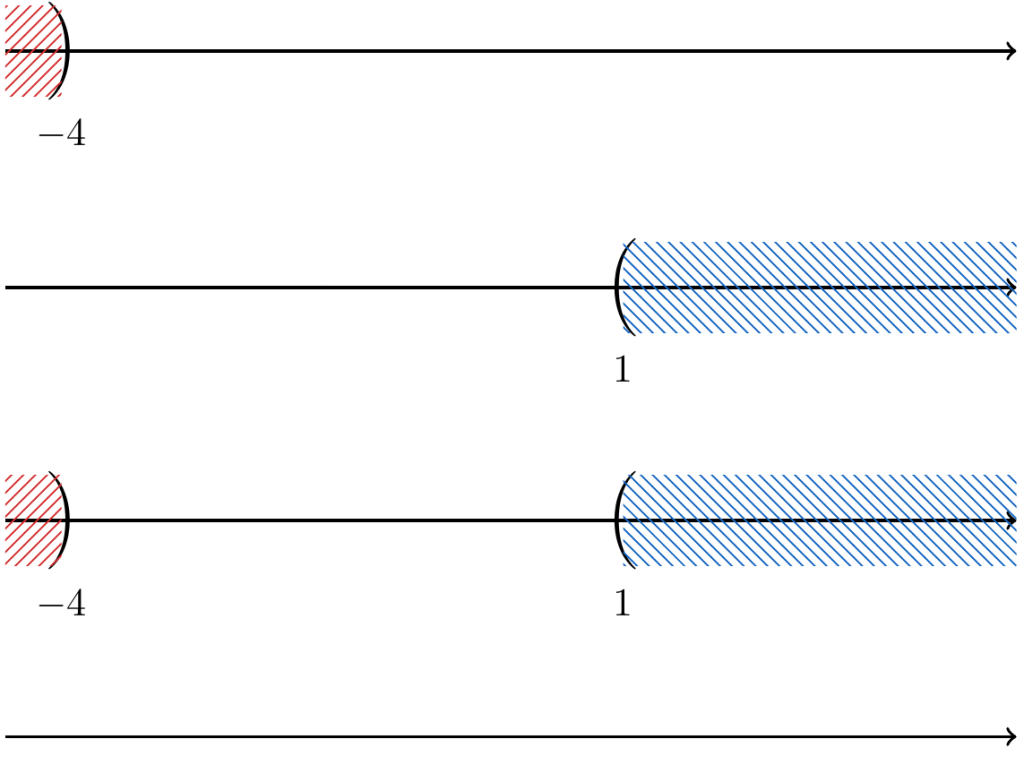
Solución Parcial:

Para determinar la solución general, debemos verificar los valores de para los cuales la expresión
es negativa, pues para estos valores, la desigualdad
siempre se cumple. Pero notemos que si unimos el conjunto que obtenemos de esta condición, independientemente de cual sea, la solución será la misma: el conjunto de los números reales
.

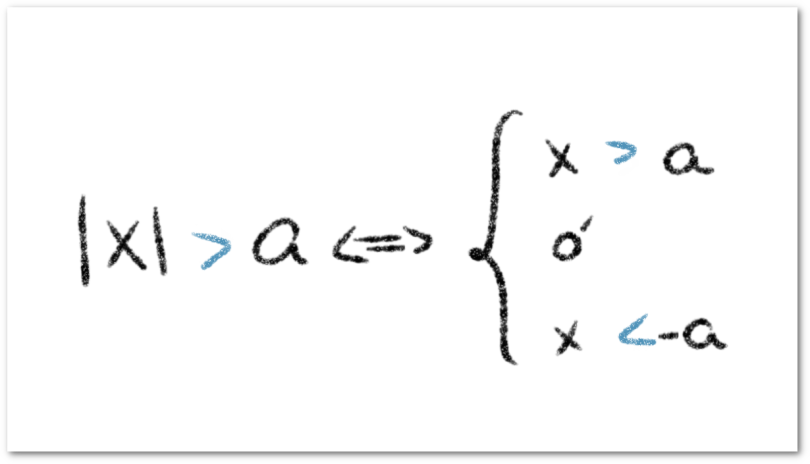


























Debe estar conectado para enviar un comentario.