Habiendo definido los cofactores de una matriz, podemos establecer un método que nos permite calcular el determinante de cualquier matriz cuadrada de tamaño .
También pudiera interesarte
El Método de Laplace
Al considerar una columna , el Método de Laplace indica que el determinante de una matriz se calcula de la siguiente manera:
En otras palabras, debemos escoger una columna, multiplicar cada elemento de la columna por su cofactor y sumar estos productos. Veamos el caso para una matriz cuadrada de tamaño tres para tener esta idea más clara, formalmente,
Podemos calcular su determinante escogiendo la primera columna y plantear la siguiente suma:
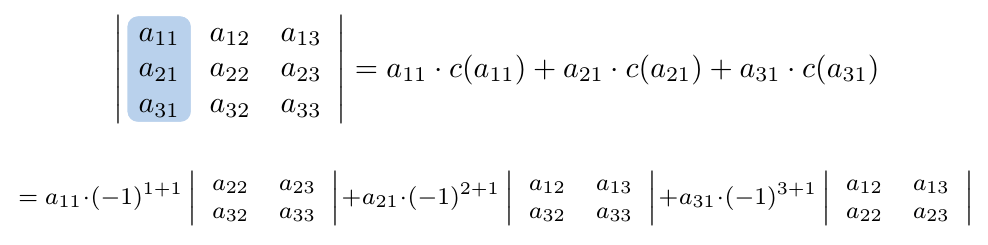
Podemos calcular su determinante escogiendo la segunda columna y plantear la siguiente suma:
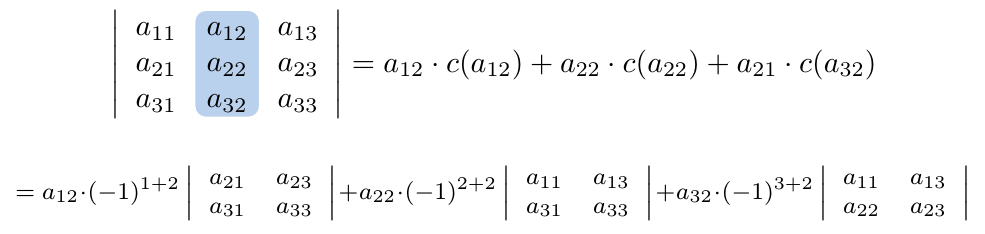
Podemos calcular su determinante escogiendo la tercera columna y plantear la siguiente suma:
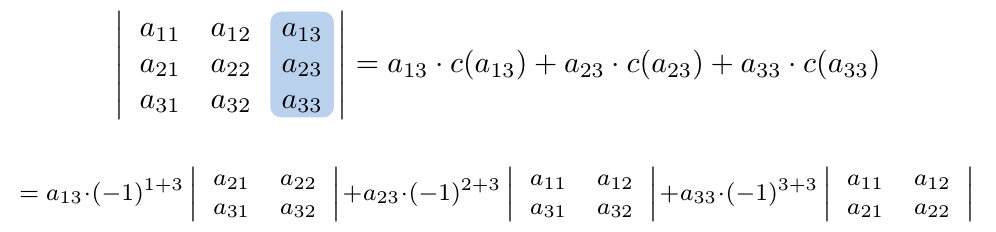
Veamos entonces, con algunos ejemplos como calcular determinantes de matrices cuadradas de tamaño tres.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 1
Considerando la matriz cuadrada de tamaño tres, calcule su determinante escogiendo la columna 2.
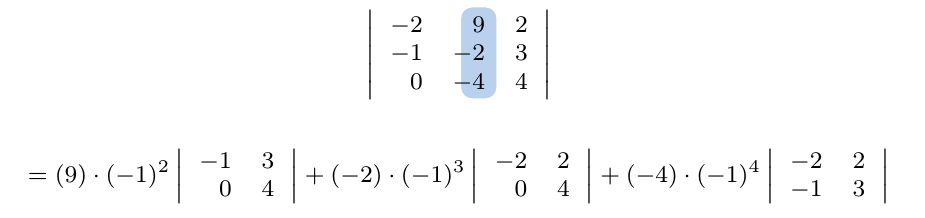
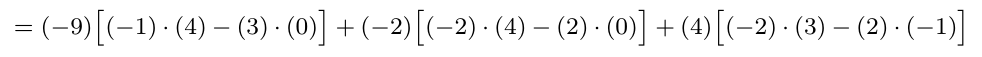
Ejemplo 2
Considerando la matriz cuadrada de tamaño tres, calcule su determinante escogiendo la columna 1.
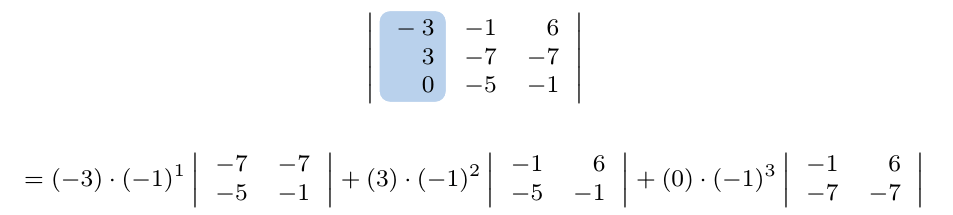

Ejemplo 3
Considerando la matriz cuadrada de tamaño tres, calcule su determinante escogiendo la columna 3.
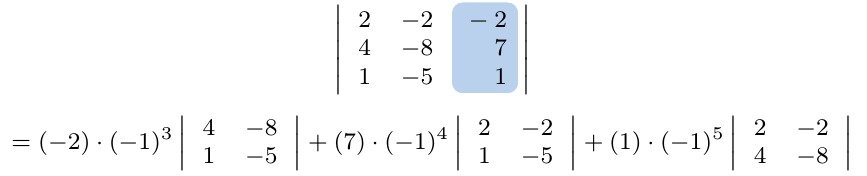
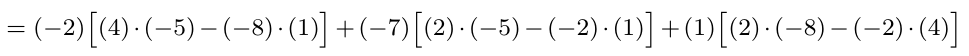
Ejemplo 4
Considerando la matriz cuadrada de tamaño tres, calcule su determinante escogiendo la columna 1.
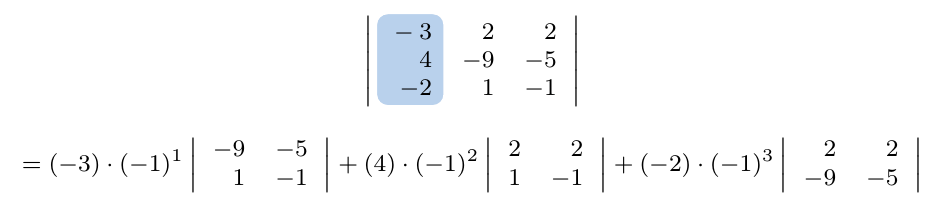
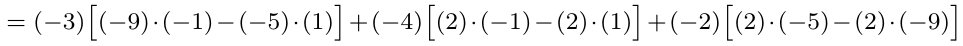
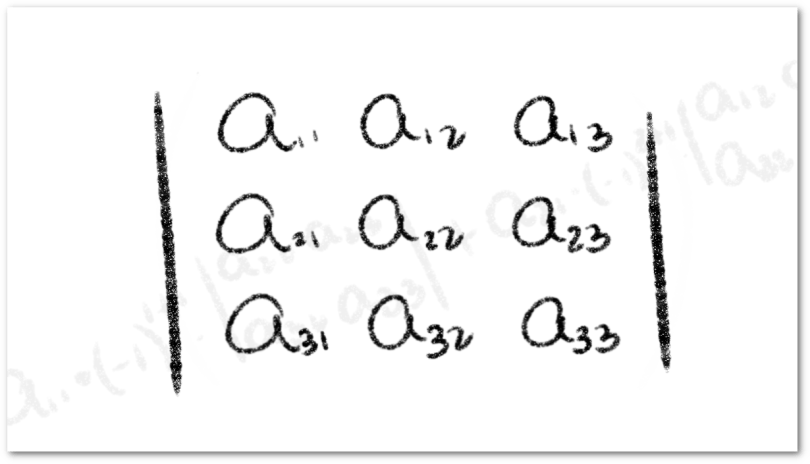
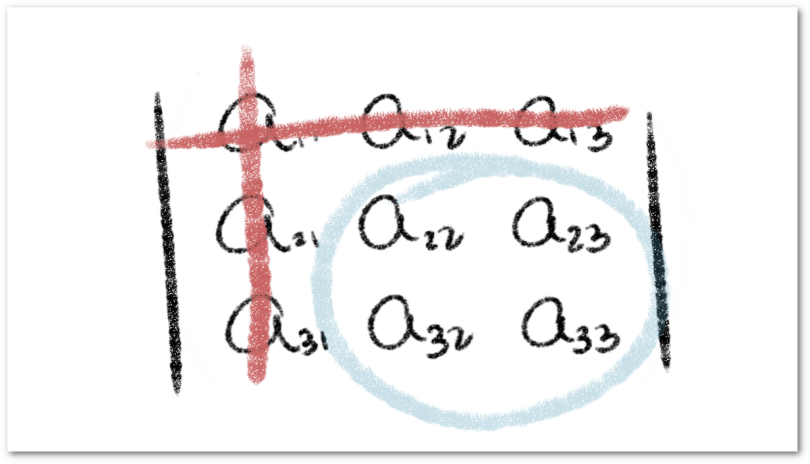

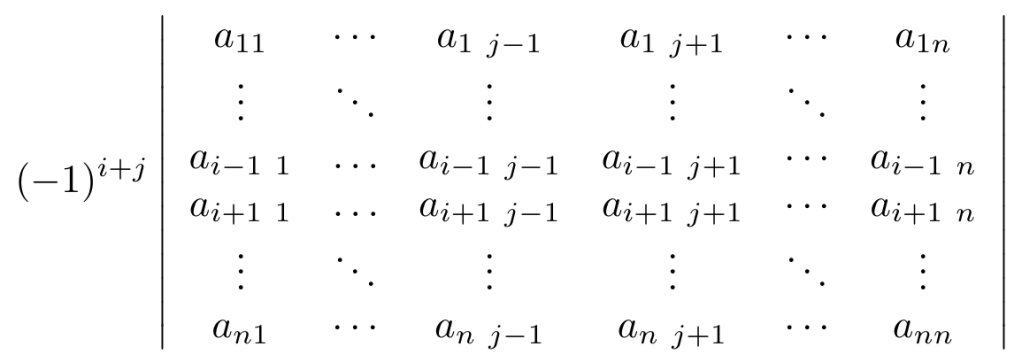










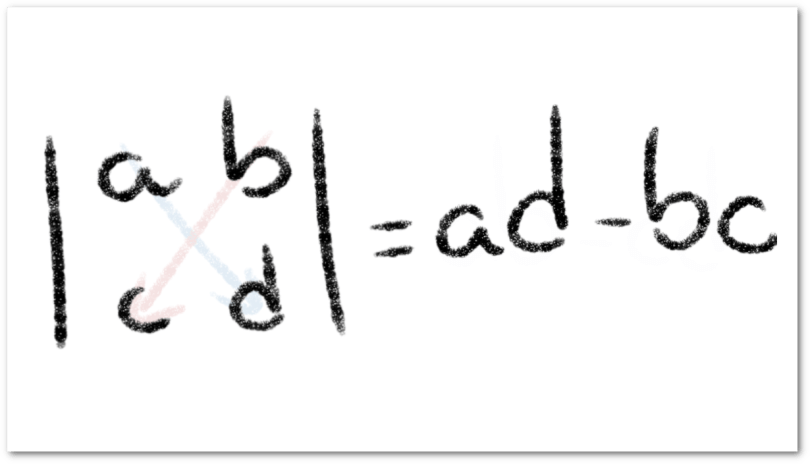
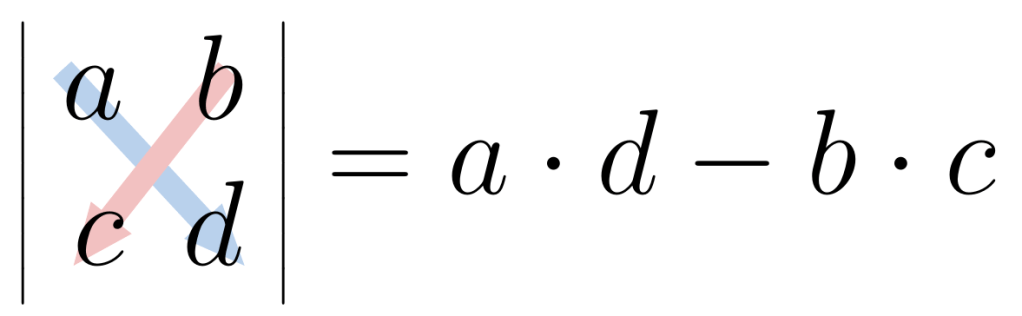
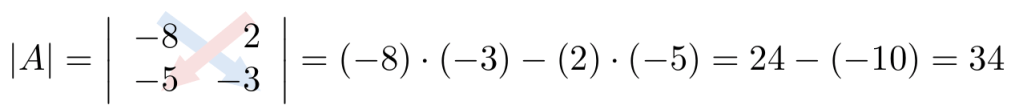
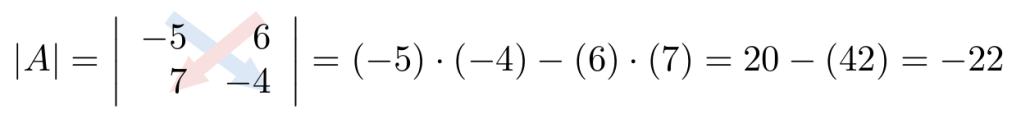
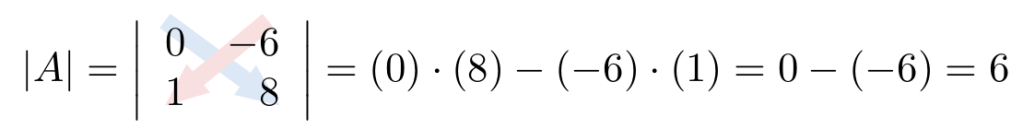
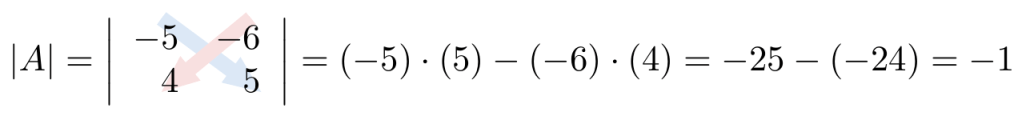












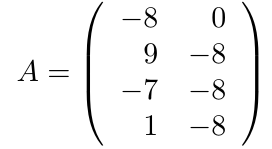


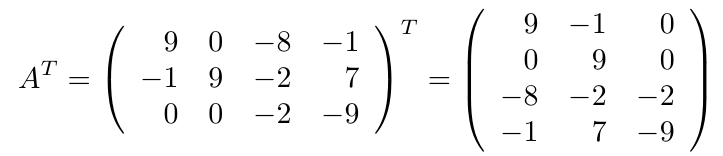
Debe estar conectado para enviar un comentario.