Receta: Almojábanas

31.01.202101.10.2021 Anthonny Arias-García2 comentarios

Las almojábanas son una especie de panecillo de queso hecho con base de almidón de yuca. En algunas regiones se conocen variedades de estas, conocidas como Pan de Bono (Colombia) o Chipa (Paraguay), esta receta es sencilla de hacer, si te gustan los bocados más salados que dulces, la textura y el aroma de las almojábanas te encantará.

Ingredientes

1 taza de leche líquida.
1/2 taza de aceite.
250gr. de Almidón de Yuca.
2 Huevos.
1 pizca de sal.
1 taza de Queso Ahumado Rallado.

También pudiera interesarte

Preparación

Se vierte la leche líquida en una olla y posteriormente se vierte el aceite.

Se mezcla y se pone en la estufa con llama alta, batiendo con suavidad de forma constante para evitar que la leche se pegue en el fondo de la olla.

Anuncios

Previamente (o paralelamente, dependiendo de sus multifuncionalidad) se vierte el almidón de yuca en un tazón. De esta forma, una vez que la leche haya alcanzado el punto de ebullición, se vierte en el tazón con almidón de yuca y se mezcla.

Una vez que la leche y el almidón se hayan mezclado bien, se vierten los dos huevos junto con la pizca de sal y se mezcla, una vez que esté todo bien incorporado, se vierte el queso ahumado y se vuelve a mezclar.

Anuncios

La mezcla, que tendrá una textura espesa, se porciona en pequeñas cantidades y se disponen en una bandeja para posteriormente hornearlas. Puede ser una bandeja plana, pero en mi caso, me gusta usar un molde para ponqués.

Se hornean a 200°C por alrededor de 20 minutos (cada horno es diferente), en mi caso particular, los últimos 3 minutos enciendo el gratinador para que queden tostaditas por encima.

Finalmente, se sacan del horno y se dejan refrescar un poco.

Operaciones entre polinomios

16.01.202107.12.2022 Anthonny Arias-García2 comentarios

Podemos definir las operaciones de suma, resta, multiplicación y división entre polinomios como una generalización de las operaciones que hemos definido entre los números reales.

También pudiera interesarte

Suma de polinomios

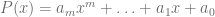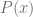Para sumar o restar polinomios, recurrimos a la propiedad asociativa de los números reales, pues agrupamos los sumandos que tengan la misma potencia de $x$ como factor, de forma que si consideramos dos polinomios $P(x) = a_m x^m + \ldots + a_1 x + a_0$ y $Q(x) = b_n x^n + \ldots + b_1 x + b_0$ , donde el grado de $P(x)$ es mayor que el grado de 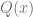$Q(x)$ , es decir, $m \geq n$ ; definimos la suma $P(x)+Q(x)$ de la siguiente forma:

De igual forma, definimos la resta $P(x)-Q(x)$ de la siguiente forma:

Notando que si el grado de 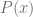$P(x)$ es estrictamente mayor que el grado de 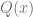$Q(x)$ , entonces completamos el polinomio 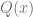$Q(x)$ con coeficientes ceros, es decir, 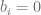$b_i = 0$ para todo $i > n$ .

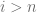Veamos con algunos ejemplos como efectuar la suma de polinomios.

Anuncios

Ejemplos

Ejemplo 1

Considerando los polinomios $P(x) = 3x^2 - 5x + 2$ y $Q(x) = 7x + 1$ , calcule la suma $P(x) + Q(x)$ .

Por lo tanto, 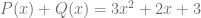$P(x) + Q(x) = 3 x^2 + 2x + 3$ .

Ejemplo 2

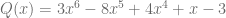Considerando los polinomios $P(x) = 4x^6 + x^4 - 2x^2 + 9x + 12$ y $Q(x) = 3x^6 - 8x^5 + 4x^4 + x - 3$ , calcule la suma $P(x) + Q(x)$ .

Por lo tanto, 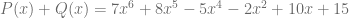$P(x) + Q(x) = 7x^6 + 8x^5 - 5x^4 - 2x^2 + 10x + 15$ .

Ejemplo 3

Considerando los polinomios $P(x) = 6x^3 + 7x^2 - 4$ y $Q(x) = 2x + 3$ , calcule la resta $P(x) - Q(x)$ .

Por lo tanto, $P(x) - Q(x) = 6x^3 + 7x^2 - 2x - 7$ .

Ejemplo 4

Considerando los polinomios 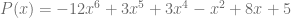$P(x) = -12x^6 + 3x^5 + 3x^4 - x^2 + 8x + 5$ y $Q(x) = x^6 + 5x^5 + 2x^4 - 4x^3 - 10x^2 - x$ , calcule la resta $P(x) - Q(x)$ .

Por lo tanto, $P(x) - Q(x) = 11x^6 - 2x^5 + x^4 + 4x^3 + 9x^2 + 9x + 5$ .

Anuncios

Producto de polinomios

Para multiplicar polinomios, recurrimos a la propiedad distributiva de los números reales, de forma que si consideramos dos polinomios 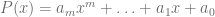$P(x) = a_m x^m + \ldots + a_1 x + a_0$ y $Q(x) = b_n x^n + \ldots + b_1 x + b_0$ , podemos definir el producto de estos dos polinomios distribuyendo los productos de la siguiente forma

Producto o Multiplicación de Polinomios | totumat.com

Una vez que se ha expandido este producto, lo podemos expresar como una sumatoria de la siguiente manera:

$\sum_{i=1}^n \sum_{j=1}^m a_i b_j x^{i+j}$

Este procedimiento pudiera resultar extenso y la notación del caso general pareciera engorrosa, sin embargo, efectuar el producto de polinomios no es más que la aplicación de la propiedad distributiva para los números reales y la posterior aplicación de las propiedades de las potencias para sumar los exponentes.

Veamos en los siguientes ejemplos como calcular algunos productos entre polinomios.

Anuncios

Ejemplos

Ejemplo 5

Considerando los polinomios $P(x) = 4 x + 3$ y $Q(x) = - 10 x - 4$ . Calcule el producto $P(x) \cdot Q(X)$ , es decir,

$\left( 4 x + 3 \right) \cdot \left( - 10 x - 4 \right)$

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

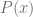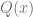Por lo tanto el producto de los polinomios $P(x)$ y $Q(x)$ es igual a

$- 40 x^{2} - 46 x - 12$

Ejemplo 6

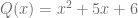Considerando los polinomios $P(x) = 6 x^{2} - 8 x + 2$ y $Q(x) = x^{2} + 5 x + 6$ . Calcule el producto $P(x) \cdot Q(X)$ , es decir,

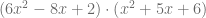
$\left( 6 x^{2} - 8 x + 2 \right) \cdot \left( x^{2} + 5 x + 6 \right)$

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

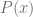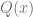Por lo tanto el producto de los polinomios $P(x)$ y $Q(x)$ es igual a

$6 x^{4} + 22 x^{3} - 2 x^{2} - 38 x + 12$

Ejemplo 7

Considerando los polinomios 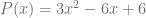$P(x) = 3 x^{2} - 6 x + 6$ y $Q(x) = - 9 x^{3} - 5 x^{2} + 4 x + 7$ . Calcule el producto $P(x) \cdot Q(X)$ , es decir,

$\left( 3 x^{2} - 6 x + 6 \right) \cdot \left( - 9 x^{3} - 5 x^{2} + 4 x + 7 \right)$

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

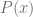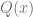Por lo tanto el producto de los polinomios $P(x)$ y $Q(x)$ es igual a

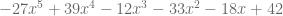
$- 27 x^{5} + 39 x^{4} - 12 x^{3} - 33 x^{2} - 18 x + 42$

Ejemplo 9

Considerando los polinomios $P(x) = - 4 x^{3} + x^{2} - 2 x + 2$ y $Q(x) = 9 x^{2} - x + 4$ . Calcule el producto $P(x) \cdot Q(X)$ , es decir,

$\left( - 4 x^{3} + x^{2} - 2 x + 2 \right) \cdot \left( 9 x^{2} - x + 4 \right)$

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

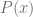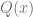Por lo tanto el producto de los polinomios $P(x)$ y $Q(x)$ es igual a

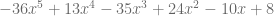
$- 36 x^{5} + 13 x^{4} - 35 x^{3} + 24 x^{2} - 10 x + 8$

Anuncios

División de polinomios

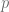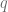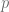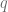Para definir la división entre polinomios, debemos hacer algunas observaciones sobre división entre números reales pues considerando $p$ y $q$ dos números enteros, al dividir $p$ entre $q$ , buscamos un número tal que al multiplicarlo por 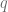$q$ el resultado sea exactamente 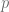$p$ , es decir, un número entero $c$ tal que

$p = c \cdot q$

En este caso, decimos que la división es exacta. Sin embargo, si no podemos encontrar este número, buscamos un número tal que al multiplicarlo por 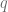$q$ , el resultado sea mayor de los enteros menores que 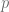$p$ , es decir, un número entero $c$ tal que

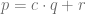
$p = c \cdot q + r$

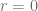Donde $0 < r < a$ . Esta propiedad se conoce como el algoritmo de la división. Al número $r$ lo llamaremos el resto de la división y se puede calcular como $r = p - c \cdot q$ . Además notemos que si la división es exacta, entonces el resto de la división es igual a cero, es decir, $r=0$ . Veamos en los siguientes ejemplos como expresar algunas divisiones usando el algoritmo de la división.

Anuncios

Ejemplos

Ejemplo 9

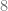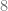Si dividimos $8$ entre $4$ , entonces buscamos un número entero tal que al multiplicarlo por $4$ el resultado sea o que está cerca de $8$ , particularmente el número que estamos buscando es 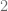$2$ pues $2 \cdot 4 = 8$ y de acuerdo con el algoritmo de la división, el resto es igual a $8 - 8 = 0$ , esto lo expresamos de la siguiente forma:

División de Números Enteros | totumat.com

Por lo tanto decimos que $8 = 2 \cdot 4 + 0$ . En este caso el resto es igual a cero, por lo tanto, decimos que la división es exacta.

Ejemplo 10

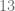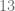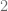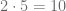Si dividimos $13$ entre $5$ , entonces buscamos un número entero tal que al multiplicarlo por $5$ el resultado sea o que está cerca de $13$ , particularmente el número que estamos buscando es $2$ pues $2 \cdot 5 = 10$ y de acuerdo con el algoritmo de la división, el resto es igual a 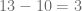$13 - 10 = 3$ , esto lo expresamos de la siguiente forma:

Por lo tanto decimos que $13 = 2 \cdot 5 + 3$ . En este caso el resto es distinto de cero, por lo tanto, decimos que la división no es exacta.

Ejemplo 11

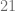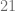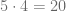Si dividimos $21$ entre $4$ , entonces buscamos un número entero tal que al multiplicarlo por $4$ el resultado sea o que está cerca de $21$ , particularmente el número que estamos buscando es $5$ pues $5 \cdot 4 = 20$ y de acuerdo con el algoritmo de la división, el resto es igual a $21 - 20 = 1$ , esto lo expresamos de la siguiente forma:

Por lo tanto decimos que $21 = 5 \cdot 4 + 1$ . En este caso el resto es distinto de cero, por lo tanto, decimos que la división no es exacta.

Ejemplo 12

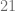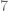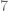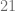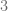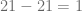Si dividimos $21$ entre $7$ , entonces buscamos un número entero tal que al multiplicarlo por $7$ el resultado sea o que está cerca de $21$ , particularmente el número que estamos buscando es $3$ pues $3 \cdot 7 = 21$ y de acuerdo con el algoritmo de la división, el resto es igual a $21 - 21 = 1$ , esto lo expresamos de la siguiente forma:

Por lo tanto decimos que 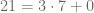$21 = 3 \cdot 7 + 0$ . En este caso el resto es igual a cero, por lo tanto, decimos que la división es exacta.

Anuncios

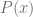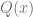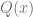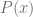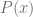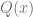El algoritmo de la división se puede generalizar al operar entre polinomios. De modo que si consideramos $P(x)$ y $Q(x)$ dos polinomios tales que el grado de $Q(x)$ es menor o igual que el grado de $P(x)$ , al dividir $P(x)$ entre $Q(x)$ , buscamos un polinomio tal que al multiplicarlo por 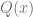$Q(x)$ el resultado sea exactamente 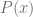$P(x)$ , es decir, un polinomio $C(x)$ tal que

$P(x) = C(x) \cdot Q(x)$

En este caso, decimos que la división es exacta. Sin embargo, si no podemos encontrar este polinomio, buscamos un polinomio tal que al multiplicarlo por 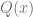$Q(x)$ el polinomio resultante tenga el mismo grado que 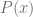$P(x)$ y que el grado del polinomio que define el resto sea menor que el grado de 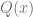$Q(x)$ , es decir, un polinomio $C(x)$ tal que

$P(x) = C(x) \cdot Q(x) + R(x)$

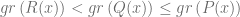Donde $gr\left( R(x) \right) < gr\left( Q(x) \right) \leq gr\left( P(x) \right)$ . Además notemos que si la división es exacta, entonces el resto de la división es igual a cero, es decir, 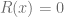$R(x) = 0$ . Veamos en los siguientes ejemplos el método para dividir polinomios y además, como expresar estas divisiones usando el algoritmo de la división.

Anuncios

Ejemplos

Ejemplo 13

Si dividimos el polinomio $P(x) = x^2 + x + 3$ entre el polinomio $Q(x) = x + 1$ , entonces los escribimos de la siguiente forma

El siguiente paso será buscar un polinomio tal que al multiplicarlo por el primer sumando del polinomio $Q(x) = x + 1$ el resultado sea exactamente igual al primer sumando del polinomio $P(x) = x^2 + x + 3$ , en este caso el polinomio que estamos buscando es $x$ y lo escribimos de la siguiente forma

El siguiente paso será multiplicar el polinomio $Q(x) = x + 1$ por $x$ y el resultado se lo restamos al polinomio $P(x) = x^2 + x + 3$ de la siguiente forma

Notamos que el grado del polinomio en el resto es menor que el grado del polinomio 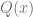$Q(x)$ , Por lo tanto, concluimos que

$x^2 + x + 3 = x \cdot (x+1) + 3$

Ejemplo 14

Si dividimos el polinomio 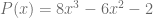$P(x) = 8x^3 - 6x^2 - 2$ entre el polinomio $Q(x) = 2x^2 + x - 1$ , entonces completamos los polinomios incompletos y los escribimos de la siguiente forma

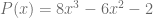El siguiente paso será buscar un polinomio tal que al multiplicarlo por el primer sumando del polinomio $Q(x) = 2x^2 + x - 1$ el resultado sea exactamente igual al primer sumando del polinomio $P(x) = 8x^3 - 6x^2 - 2$ , en este caso el polinomio que estamos buscando es 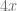$4x$ y lo escribimos de la siguiente forma

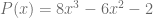El siguiente paso será multiplicar el polinomio $Q(x) = 2x^2 + x - 1$ por $x$ y el resultado se lo restamos al polinomio $P(x) = 8x^3 - 6x^2 - 2$ de la siguiente forma

Notamos que el grado del polinomio en el resto es menor que el grado del polinomio 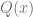$Q(x)$ , por lo tanto, el siguiente paso será buscar un polinomio tal que al multiplicarlo por el primer sumando del polinomio $Q(x) = 2x^2 + x - 1$ el resultado sea exactamente igual al primer sumando del polinomio en el resto, de decir, el polinomio $-10x^2 + 4x$ .

En este caso el polinomio que estamos buscando es 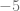$-5$ y lo multiplicamos por el polinomio $Q(x) = 2x^2 + x - 1$ ; el resultado se lo restamos al polinomio $-10x^2 + 4x$ de la siguiente forma

Notamos que el grado del polinomio en el resto es menor que el grado del polinomio 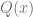$Q(x)$ , Por lo tanto, concluimos que

$8x^3 - 6x^2 - 2 = (4x-5) \cdot (2x^2 + x - 1) + 9x-7$

Memes Matemáticos – Diciembre 2020

04.01.202112.04.2021 Anthonny Arias-GarcíaDeja un comentario

La popularidad de un meme refleja la forma en que la sociedad comprende un hecho y las matemáticas no se escapan de esto, pues la comunidad matemática en las redes sociales ha aumentado su presencia en los últimos meses. Llegamos (con vida) al final del infame año 2020 y traemos para ti una compilación de los mejores memes matemáticos de Diciembre 2020.

También pudiera interesarte

¿Por qué los matemáticos fallan las pruebas de Coeficiente Intelectual?

Hay situaciones que tienen una solución simple, pero algunas personas sobre dimensionan los problemas. Este es el caso de esta sencilla secuencia numérica, tal como lo expone el usuario u/MostCharmingChicken. En la imagen se puede leer:

Descanso de matemáticas!
1,3,5,7,…
¿Qué número sigue?

217341, porque si
$f(x)=\frac{18111}{2} x^4 - 90555 x^3$
$+ \frac{633885}{2} x^2 - 452773x + 217331$
entonces:

$f(1)=1$
$f(2)=3$
$f(3)=5$
$f(4)=7$
$f(5)=217341$

+C

Uno de los memes más repetidos en las matemáticas, es el que nos recuerda que debemos sumar $C$ después de calcular la integrales, esto se debe a que al calcular la integral de una función, estamos calculando toda la familia de antiderivadas. El usuario u/SalazarRED, nos trae este meme (de antaño, memísticamente hablando).

$\int aspiri \ dn = aspirin + C$

Anuncios

Nadie puede escribir ξ

Si bien muchos de nosotros sufrimos durante los estudios de educación primaria para que nuestra escritura fuera más que garabatos con tediosas lecciones de caligrafía, pocos son los que en el ámbito de las matemáticas, logran escribir de una forma agradable a la vista, la letra ξ (Xi) del alfabeto griego.

Nueva contraseña
Sgdk178&_2oS
débil

Nueva contraseña
ξ
Fuerte

La opinión de los demás

Si bien es cierto que ninguna opinión es inválida y todos tienen derecho a expresarse, hay cosas que dice la gente que no tiene sentido alguno. Esto es lo que expone el usuario u/FaGa_44. En la imagen se puede leer

«Debes que respetar la opinión de los demás»

La opinión de los demás

$3^3 = 6$

Anuncios

La calculadora de los teléfonos

Si bien hoy en día se pueden encontrar potentes calculadoras navegando en la red o como aplicaciones para los celulares. Las calculadoras nativas de los teléfonos que inicialmente parecen calculadoras bodegueras, su rango de operaciones puede ampliarse cuando se posiciona el teléfono de forma horizontal. Esto es lo que expone el usuario u/officiallyaninja. En la imagen se puede leer:

Las calculadoras en los teléfonos son como

El cero no es un número natural

Si desean generar una discusión aireada cuando estén hablando con un grupo de matemáticos, pregunten si el cero es un número natural. Si bien, considerar el cero como un número natural puede facilitar con grandiosidad las demostraciones matemáticas, este usualmente no se considera como natural por la forma en que está definido. Esto es lo que expone el usuario u/12_Semitones, asociando esta situación a una escena icónica del universo de Star Wars. En la imagen se puede leer:

Primer Panel

$\mathbb{N}$

Tú estás en el Concejo de los Enteros, pero no de podemos otorgar el título de Número Natural.

Segundo Panel

$0$

¿Qué? ¡Esto es indignante! ¡No es justo!

El principal argumento que se usa para excluir al cero de los números naturales es que los números naturales se usan para contar, y el cero no denota ninguna cantidad. El usuario u/12_Semitones, también hace referencia a esta discusión. En la imagen se puede leer:

En la izquierda de la imagen

En la derecha de la imagen

Una persona diciendo que cero no es un número porque es la ausencia de una cantidad no es una cantidad.

Anuncios

Integrar por Partes

Al calcular la integral de una función, uno de los métodos más potentes es el Método de Integración por Partes y en muchas ocasiones ocurre que al aplicar el método, la integral resultante también requiere que se aplique nuevamente el método. Esto es lo que expone el usuario u/Focal-Point1.

Primer Panel

Yo (Moe) integrando por partes (botando a Barney del bar.)

Segundo Panel

Yo (sacudiéndome las manos)

Tercer Panel

Otro método de integración por partes (Barney otra vez en el bar)

¿Convertir a pi en un racional?

Dividir cualquier número real distinto de cero entre él mismo, da el número uno como resultado. Esto es lo que expone el usuario u/sewingshark. En la imagen se puede leer:

$\frac{\pi}{\pi}$

$\pi$ : me estás pidiendo que sea racional.

Anuncios

La derivada de la función exponencial

Al definir las reglas para calcular derivadas, podemos notar que la derivada de la función exponencial $\textit{\large e}^x$ es exactamente ella misma. Sin embargo, al calcular derivadas parciales, la situación puede cambiar pues dependiendo de la variable, esta derivada puede ser igual a cero. Esto es lo que exponen los usuarios u/12_Semitones y u/TheXray02, respectivamente.

Llegamos al 2021… ¿Qué puede salir mal?

Hay un dicho que no me gusta porque tiende a desalentar a los estudiantes de matemáticas infundiendo temor sobre el cálculo de integrales, pero lo citaré para presentar el contexto de este meme, dice así: «deriva el que sabe, integra el que puede». Si bien es mero prejuicio contra las hermosas integrales, este meme que presenta el usuario u/12_Semitones lo resume todo pues nos muestra como cambiar ligeramente la función que estamos integrando, puede complicar nuestros cálculos.

¿Crees que se nos escapó un meme? ¡Comparte tu mejor meme en los comentarios!

Funciones Cuadráticas

02.01.202107.12.2022 Anthonny Arias-García1 comentario

Una vez que hemos definido las transformaciones de funciones elementales, podemos considerar la función cuadrática para sentar la base de un tipo de funciones que se generan a partir de ellas, conocidas la forma canónica de la función cuadrática, expresadas de la siguiente forma

$f(x) = (px + q)^2 + r, \ p \neq 0$

Estas expresiones pueden expandirse para definir la forma general de la ecuación cuadrática, de la siguiente forma

$f(x) = ax^2 + bx + c, \ a \neq 0$

En general, estas funciones son llamadas Funciones Cuadráticas y notemos que esta expresión es la misma que define a las ecuaciones cuadráticas. La gráfica de esta función se conoce como parábola y su forma depende de los coeficientes $a$ , $b$ y $c$ .

Anuncios

Concavidad de la función cuadrática

Gráficamente, diremos que una parábola es convexa (o cóncava hacia arriba), si la apertura de esta apunta hacia arriba, es decir, si tiene la forma $\cup$ ; por otra parte, diremos que una parábola es cóncava (o cóncava hacia abajo), si la apertura de esta apunta hacia abajo, es decir, si tiene la forma $\cap$ .

Considerando la función $f(x) = ax^2 + bx + c$ , diremos que $a$ es el coeficiente principal y la concavidad de esta función estará definida de la siguiente forma:

Si $a > 0$ entonces la función cuadrática es convexa.
Si $a < 0$ entonces la función cuadrática es cóncava.

Concavidad de la función cuadrática | totumat.com

Vértice de la función cuadrática

Diremos que el máximo de una función es un punto $x_0$ tal que $f(x_0) > f(x)$ para todo valor de $x$ en el conjunto de los números reales, análogamente, iremos que el mínimo de una función es un punto $x_0$ tal que $f(x_0) < f(x)$ para todo valor de $x$ en el conjunto de los números reales. Estos puntos se conocen como extremos de una función.

Habiendo determinado la concavidad de una función cuadrática, podemos notar que esta alcanza un extremo de la siguiente forma:

Si la función cuadrática es convexa, entonces ésta alcanza un mínimo.
Si la función cuadrática es cóncava, entonces ésta alcanza un máximo.

Al extremo de una función cuadrática se le conoce como el vértice y es posible calcular las coordenadas que definen a este punto considerando la forma canónica pues notando que el vértice de la función cuadrática $f(x)=x^2$ se encuentra en el punto $(0,0)$ .

Al transformar esta función, podemos concluir que la expresión $(px + q)^2 + r$ traslada a la función $x^2$ en $-\frac{q}{p}$ unidades en el Eje X y en $r$ unidades en el Eje Y. Particularmente, el vértice estará trasladado hasta el punto $\left( -\frac{q}{p} , r \right)$ .

Vértice de la función cuadrática | totumat.com

Veamos como a partir de este hecho, podemos calcular las coordenadas del vértice de una función cuadrática expresada en su forma general.

Anuncios

Coordenada del vértice en el Eje X

Expandiendo la forma canónica podemos obtener la forma general de la función cuadrática y así, establecer una igualdad entre los coeficientes correspondientes, como sigue

Si la coordenada en el Eje X del vértice está denotada por $V_x$ , entonces podemos plantear el siguiente sistemas de ecuaciones.

$a = p^2$

$b = 2pq$

$V_x = -\frac{q}{p}$

A partir de la segunda ecuación podemos despejar $q$ para obtener que $q=\frac{b}{2p}$ y sustituyendo este valor de $q$ en la tercera ecuación, tenemos que

$V_x \ = \ -\frac{q}{p}$

$\ = \ -\frac{ \ \frac{b}{2p} \ }{p}$

$\ = \ -\dfrac{ \ b \ }{2p^2}$

Entonces, considerando esta última igualdad y que $a = p^2$ , concluimos que la coordenada en el Eje X de la función cuadrática $f(x) = ax^2 + bx + c$ es

$V_x = -\dfrac{ \ b \ }{2a}$

Coordenada del vértice en el Eje Y

Para calcular la coordenada en el Eje Y del vértice, basta con evaluar la función $f(x) = ax^2 + bx + c$ en $V_x = -\dfrac{ \ b \ }{2a}$ .

$f \left( V_x \right) \ = \ a\left( V_x \right)^2 + b \left( V_x \right) + c$

$\ = \ a\left( -\dfrac{ \ b \ }{2a} \right)^2 + b \left( -\dfrac{ \ b \ }{2a} \right) + c$

$\ = \ a \dfrac{ \ b^2 \ }{4a^2} - \dfrac{ \ b^2 \ }{2a} + c$

$\ = \ \dfrac{ \ b^2 \ }{4a} - \dfrac{ \ b^2 \ }{2a} + c$

$\ = \ \dfrac{ \ b^2 \ }{4a} - \dfrac{ \ 2b^2 \ }{4a} + \frac{4ac}{4a}$

$\ = \ \dfrac{b^2 - 2b^2 + 4ac}{4a}$

$\ = \ \dfrac{-b^2 + 4ac}{4a}$

De esta forma, concluimos que la coordenada en el Eje Y de la función cuadrática $f(x) = ax^2 + bx + c$ es

$V_y = \dfrac{-b^2 + 4ac}{4a}$

Anuncios

Eje de Simetría de la Función Cuadrática

Una de las características que más destaca al observar la gráfica de una función cuadrática, es decir, una parábola, es que esta crece de forma simétrica respecto a un eje, a este eje lo llamamos eje de simetría y una vez que hemos calculado el vértice de una función cuadrática, definimos este eje como la recta vertical definida por la siguiente ecuación:

$x = V_x$

Eje de Simetría de la Función Cuadrática | totumat.com

Puntos de Corte de la Función Cuadrática

Con el Eje Y

Para calcular el punto de corte con el Eje Y, basta con evaluar la función en el punto $x=0$ , es decir, calcular la imagen $f(0) = a(0)^2 + b(0) + c$ .

Puntos de Corte de la Función Cuadrática | totumat.com

Con el Eje X

Si bien una función cuadrática definida en todos los números reales tendrá un punto de corte con el Eje Y, no siempre podemos garantizar que esta tenga un punto de corte en el Eje X. Veamos a continuación los tres casos posibles que podemos encontrar al estudiar los puntos de corte con el Eje X.

Para calcular los puntos de corte con el Eje X, debemos calcular los valores de $x$ para los cuales $f(x) = 0$ , es decir, para los cuales se satisface la ecuación cuadrática $ax^2 + bx + c = 0$ . Para determinar la solución de esta ecuación definimos su discriminante como la expresión $b^2-4 \cdot a \cdot c$ y éste número nos determina la cantidad de puntos de corte con el Eje X, de la siguiente manera:

Si $b^2-4 \cdot a \cdot c > 0$ , entonces existen dos puntos de corte.
Si $b^2-4 \cdot a \cdot c = 0$ , entonces existe sólo un punto de corte.
Si $b^2-4 \cdot a \cdot c < 0$ , entonces no tiene puntos de corte.

A partir del discriminante podemos definir una fórmula conocida como el Método del Discriminante que permite calcular los valores de $x$ que satisfacen la ecuación cuadrática, de la siguiente forma:

$\dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a}$

Receta: Hallacas

22.12.202002.12.2022 Anthonny Arias-GarcíaDeja un comentario

La hallaca es el plato típico de la navidad venezolana, y aunque en cada país de Latinoamérica existen platos similares, cada uno tiene su propia sazón e identidad cultural. La hallaca también varía dentro de Venezuela pues dependiendo de la región en que uno se encuentre, puede encontrar una u otra versión. En esta ocasión les comparto la Receta de la Hallaca Andina, la más simple de todas las versiones andinas, pero que es muy rica en sabor.

Como anécdota personal comento que la primera vez que mi mamá hizo hallacas cuando se independizó, una señora le enseñó la receta (la Sra. Consuelo, que por cierto, hacía unas arepas riquísimas) a mi mamá cuando ella fue profesora en una zona rural del Estado Mérida y esta ha sido la receta que hemos seguido en mi casa desde que yo tengo uso de razón.

Esta receta alcanza para hacer 60 hallacas de 6-7 cm de ancho y 14-16 cm de largo, queda a su criterio decir si son pequeñas o medianas, pero con toda seguridad, no son grandes.

También pudiera interesarte

Ingredientes

Aceite Onotado
- 1 litro Aceite vegetal (preferiblemente aceite de maíz).
- 100 gr. de Onoto

Guiso
- 1/2 Kg. de Cebollín
- 2 Cebollas
- 2 Cabezas de Ajo
- 2 Pimentones Rojos
- 1/4 Kg. de Ají Dulce (Rojo)
- 1 Tallo de Ajo Porro (sólo lo blanco)
- 1 Tallo de Apio España.
- 1 Kg. de Carne de Res en Bistec
- 4 Muslos de Pollo deshuesados
- 4 Tiras de Tocineta Ahumada
- 1/2 Kg. de Pulpa de Cochino
- Sal, oregano y laurel al gusto

Masa
- Caldo de Huesos de Pollo
- 2 Cubitos
- 1 Kg. de Harina PAN (De Maíz Amarillo)
- Sal al gusto

Para armar la hallaca
- 100 gr. de Pasas
- 100 gr. de Aceitunas
- 3 Kg. de Hojas Para Hallacas Arregladas
- 1 Rollo de Hilo Pabilo

Anuncios

Preparación

Preparación del Aceite

La preparación para este tipo de hallacas dura al menos dos días, durante el primer día se prepara el guiso. Lo primero que hay que hacer es tintar el aceite (o pintar), para esto debemos sofreír durante unos 4 minutos con llama muy baja el onoto en un sartén con unos unos 100 ml de aceite. La idea es que el onoto suelte su color para que el aceite se torne rojo intenso.

Esta fotografía incluye una arepa porque estaba haciendo desayuno.

Una vez que el aceite tiene ese color rojo intenso, ser vierte dentro la botella de aceite para que todo el litro de aceite para que todo el resto del aceite se tinte, esto también se conoce como onotar el aceite.

Anuncios

Preparación del Guiso

Una vez que ya se ha tintado el aceite procedemos a picar las carnes en cuadritos (no muy pequeños), es decir, picamos la carne de res en bistec, la pulpa de cochino, el pollo y la tocineta.

Una vez que se han picado todas las carnes, se vierten en un bowl grande y se mezclan.

Anuncios

Para procesar los aliños, se empieza por pelar los ajos y licuarlos con el aceite onotado, el puré de ajo se sofríe por cuatro minutos, se deja enfriar (importante para que no se cocine la carne con el calor del sofrito); posteriormente se incorpora al bowl y se mezcla.

Se pica el Apio España, se sofríe con aceite onotado por cuatro minutos, se deja enfriar (importante para que no se cocine la carne con el calor del sofrito); posteriormente se incorpora al bowl y se mezcla.

Se pica el Ajo Porro, se sofríe con aceite onotado por cuatro minutos, se deja enfriar (importante para que no se cocine la carne con el calor del sofrito); posteriormente se incorpora al bowl y se mezcla.

Se pica la Cebolla, se sofríe con aceite onotado por cuatro minutos, se deja enfriar (importante para que no se cocine la carne con el calor del sofrito); posteriormente se incorpora al bowl y se mezcla.

Se pica el Cebollín, se sofríe con aceite onotado por cuatro minutos, se deja enfriar (importante para que no se cocine la carne con el calor del sofrito); posteriormente se incorpora al bowl y se mezcla.

Se pica el Ají Dulce, se sofríe con aceite onotado por cuatro minutos, se deja enfriar (importante para que no se cocine la carne con el calor del sofrito); posteriormente se incorpora al bowl y se mezcla.

Se pica el Pimentón, se sofríe con aceite onotado por cuatro minutos, se deja enfriar (importante para que no se cocine la carne con el calor del sofrito); posteriormente se incorpora al bowl y se mezcla.

Finalmente, se mezcla todo y se deja reposar en la nevera hasta el otro día.

Anuncios

Preparación de la Masa

La parte más importante de la preparación de la masa es el sabor que le demos al agua que se va a usar, eso por esto que se debe hacer un caldo de huesos de pollo y dejarme que el agua merme un poco para que el sabor se concentre.

Tuve que cambiar el pollo a una olla porque debía usar el caldero.

Una vez que el caldo de pollo está listo, se pasa a un bowl grande donde se preparará la masa, se le agregan dos cubitos desmenuzados y al menos media taza de aceite onotado, mientras más aceite, más amarilla quedará la masa al final, aunque también tendrá más sabor a onoto, así que hay que encontrar el equilibrio. Una vez que esto esté mezclado, se agrega una cucharada de sal y se mezcla.

Posteriormente, se empieza a verter la harina poco a poco mientras se mezcla para evitar que se empelote (es decir, que la harina forme cúmulos de masa pequeños). Si desea, puede agregar un poco de harina de maíz blanco para darle cuerpo a la masa pues la harina de maíz blanco es más fina que la harina de maíz amarillo.

Es importante mezclar con insistencia para que la masa quede con la textura ideal, puede empezar con un batidor mientras la masa está líquida pero al finalizar es mejor mezclar a mano pues el volumen de masa que se genera es muy grande. La contextura final debería ser blanda pero a la vez maleable.

La contextura que se debería conseguir es la siguiente:

Más o menos esta textura para la masa. #Hallacas. pic.twitter.com/hl545XPdCy
— Anthonny sin luz en cuarentena (@AnthonnyAG) December 12, 2020

Anuncios

Armar las Hallacas

El primer paso para armar las hallacas es escoger y arreglar las hojas, y aunque se pueden conseguir en los supermercados ya arregladas (como en el caso de esta receta), lo ideal es usar las hojas que estén bien ahumadas (es decir, que no estén verde vibrante) y que sean grandes (el tamaño ideal para mí es 40cm de ancho y 40cm de largo), se les corta la hebra principal pues esta por ser dura puede quebrar las hojas cuando estas se doblan.

Una vez escogidas las hojas, se deben lavar una a una con agua y esponja (use jabón sólo si tienen mal olor), posteriormente se deben secar una a una y terminar de arreglarlas de ser necesario.

Una vez que las hojas están listas, se prepara el armado de las hallacas. En este caso se hace un armado simple que consta sólo de masa, guiso, aceitunas, pasas y aceite onotado.

Anuncios

Para armar las hallacas se debe colocar una hoja sobre la mesa de trabajo de modo que la parte lisa quede hacia arriba pues si las hebras quedan apuntando hacia arriba, la hallaca queda marcada por estas una vez que se envuelvan. Sobre la hoja se vierte una cucharadita de aceite onotado y sobre el aceite una bolita de masa.

La bolita de masa se extiende sobre la hoja, puede hacerlo con la mano o en mi caso, pongo un plástico sobre la masa, la aplasto suavemente con un plato y termino de extender con la mano de ser necesario.

Sobre la masa extendida se coloca una cucharada (generosa) de guiso, con cuidado que no se derrame fuera de la masa. Sobre el guiso se colocan aceitunas y pasas al gusto, aunque mi parecer, una aceituna y dos pasas está más que bien. Finalmente, se vierte una cucharadita de aceite onotado para mantener el guiso húmedo dentro de la hallaca mientras se cocina.

En las fotos no se aprecia bien, pero los colores no son tan pálidos, son más vibrantes.

Una vez que se ha armado la hallaca, viene el paso más importante: la envoltura y el amarrado. La importancia de este paso es que si una hallaca está mal envuelta o mal amarrada, se puede derramar mientras se cocina o se puede llenar de agua de la olla (esa agua es asquerosa).

Anuncios

La hallaca se debe envolver dos veces y las dos envolturas son diferentes, en el siguiente video muestro como hacer la primera envoltura de las hallacas.

Cómo envolver la hallaca. pic.twitter.com/MkmLPivLU6
— Anthonny sin luz en cuarentena (@AnthonnyAG) December 12, 2020

En el siguiente video muestro como hacer la segunda envoltura de las hallacas.

Cómo hacer la segunda envoltura de la hallaca. pic.twitter.com/Onw4RpZeb0
— Anthonny sin luz en cuarentena (@AnthonnyAG) December 12, 2020

Para facilitar la hechura de las hallacas, lo ideal es trabajar en serie. Una vez que se tiene la primera envoltura de un lote de hallacas, se hace la segunda envoltura y se va haciendo un lote con doble envoltura para posteriormente amarrar.

Una vez que las hallacas tiene las dos primeras envolturas, se procede a amarrarlas. En el siguiente video se muestra como amarrar correctamente una hallaca:

Cómo amarrar las #hallacas. pic.twitter.com/rYLtdevMsd
— Anthonny sin luz en cuarentena (@AnthonnyAG) December 12, 2020

Una vez amarradas las hallacas se ponen a hervir en una olla grande, una vez que el agua alcanza el punto de ebullición, se cuentan dos horas antes de apagar la ollas y sacarlas.

Anuncios

Las hallacas se deben dejar escurriendo para que boten el agua acumulada de la cocción, es importante que estén en una superficie planta para que no se deformen, y una vez que hayan enfriado, se guardan en la nevera, la idea es que los sabores se concentren, aunque normalmente la tentación es muy grande y uno se come una hallaca recién bajada de la olla.

Una vez que ya refrigeraron y los sabores se concentraron, se calientan en agua hirviendo, se abren y se comen. ¡Buen provecho!