R, lo básico.

14.04.202107.12.2022 Anthonny Arias-García4 comentarios

Una vez que hemos descargado e instalado R, podemos empezar a trabajar en él, pero antes debemos identificar algunos de sus elementos para entender la forma en que le daremos instrucciones a la computadora para que haga los cálculos para nosotros.

También pudiera interesarte

La interfaz gráfica de R

R es el programa que toma las instrucciones que le demos a la computadora y las ejecuta, y aunque lo ideal es que nos leyera la mente o que escuchara las órdenes que le damos a través de comandos de voz, esta no es la realidad. Es por esto que al instalar el programa, también se provee una interfaz gráfica donde podemos escribir las instrucciones que le queremos dar.

Ubicando el acceso directo de R en nuestro escritorio, hacemos doble click en él para abrir el programa.

Lo primero que veremos al abrirse el programa es la interfaz gráfica de R y en ella podemos identificar una ventana con un texto que consta con información sobre la versión que estamos usando, la licencia y algunos tips. Este espacio es conocido como: la consola.

Consola

La consola es el espacio donde le daremos las instrucciones a R para que haga los cálculos por nosotros. Notemos que en ella hay un símbolo «>» de color rojo, es ahí donde aparecerán las instrucciones que queremos dar, y de hecho, empecemos por darle nuestra primera instrucción: calcule la suma dos más dos.

Para esto, escribimos lo siguiente:

2+2

En su pantalla debería aparecer:

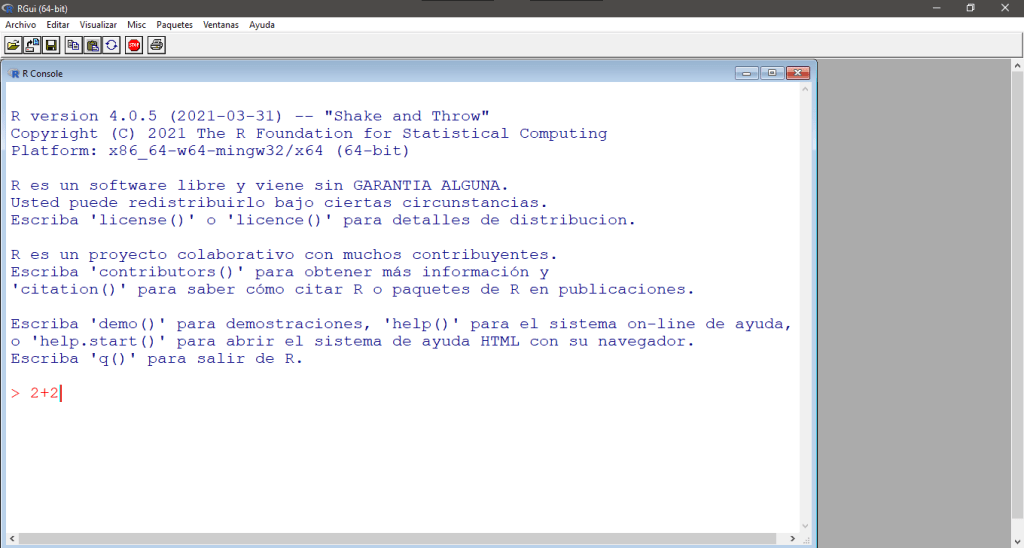
Para ejecutar la instrucción presionamos la tecla ENTER e inmediatamente debemos ver el resultado.

> 2+2
[1] 4

En su pantalla debería aparecer:

Operaciones básicas

Perfecto, ya hemos ejecutado nuestra primera instrucción en R y si bien, es una tarea sencilla como una suma, veremos que podemos efectuar más operaciones y también instrucciones más complejas. Por ejemplo, si queremos calcular el resultado de la operación

$\dfrac{-3+\sqrt{3^2-4 \cdot 5 \cdot (-2) }}{10}$

Antes, debemos entender cómo se indican las operaciones básicas en R:

La suma se indica con +
La resta se indica con –
El producto se indica con *
La división se indica con /
La potencia se indica con ^
La raíz cuadrada se indica con sqrt()
Se agrupan operaciones con ()

Sabiendo esto, para efectuar la operación, escribimos lo siguiente:

(-3+sqrt(3^3-4*5*(-2)))/10

Para ejecutar la instrucción presionamos la tecla ENTER e inmediatamente debemos ver el resultado.

> (-3+sqrt(3^3-4*5*(-2)))/10
[1] 0.5185353

En su pantalla debería aparecer:

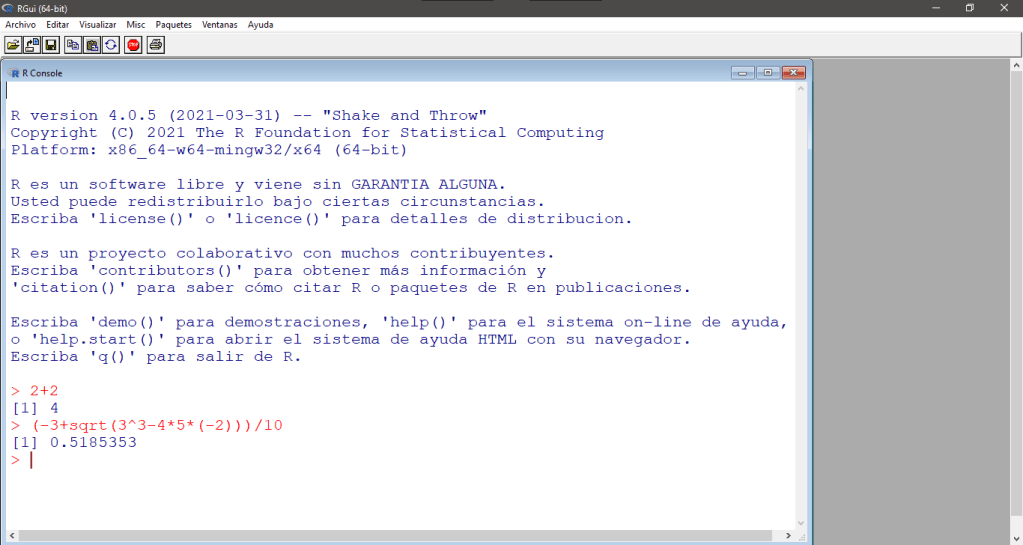
Variables

Es común que al toparnos con operaciones engorrosas de escribir, resulte necesario volverlas a efectuar para usar el resultado que estas producen, por lo que resulta necesario almacenarlas en un espacio de la memoria. Para esto definimos las variables.

Una variable nos provee un espacio de almacenamiento que puede ser nombrado para posteriormente ser manipulado para generar resultados más complejos y si bien, podemos almacenar en ella el resultado de algunas operaciones básicas, a medida que aprendemos más sobre el uso de R, veremos que podemos almacenar otro tipo de elementos.

El nombre que le demos a una variable puede contener letras, números, puntos o subguiones; por ejemplo: var, PIB, M0, M1, M2, casas_3 o media.edad. Supongamos que queremos almacenar el resultado de la operación 2+2 en una variable llamada var, entonces escribimos lo siguiente:

var <- 2+2

Para ejecutar la instrucción presionamos la tecla ENTER, en su pantalla debería aparecer:

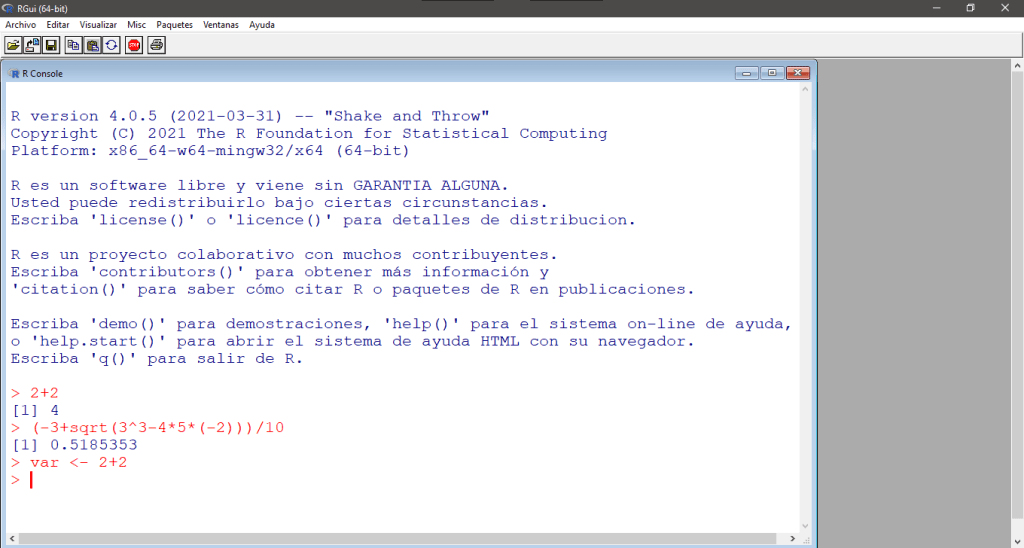
Esto es lo que se conoce como definir una variable, la instrucción «<-» denota una flecha esto quiere decir que a la variable var le estamos almacenando el resultado de la operación 2+2. Aunque otra forma de definir una variable es usando el signo de igualdad «=», entonces para definir esta variable, podemos escribir lo siguiente:

var = 2+2

Para ejecutar la instrucción presionamos la tecla ENTER, en su pantalla debería aparecer:

Una vez que hemos definido una variable, podemos utilizarla para operaciones más complejas. Por ejemplo, si al resultado que hemos almacenado en la variable var le queremos sumar seis, entonces escribimos

var+6

Para ejecutar la instrucción presionamos la tecla ENTER e inmediatamente debemos ver el resultado.

> var+6
[1] 10

En su pantalla debería aparecer:

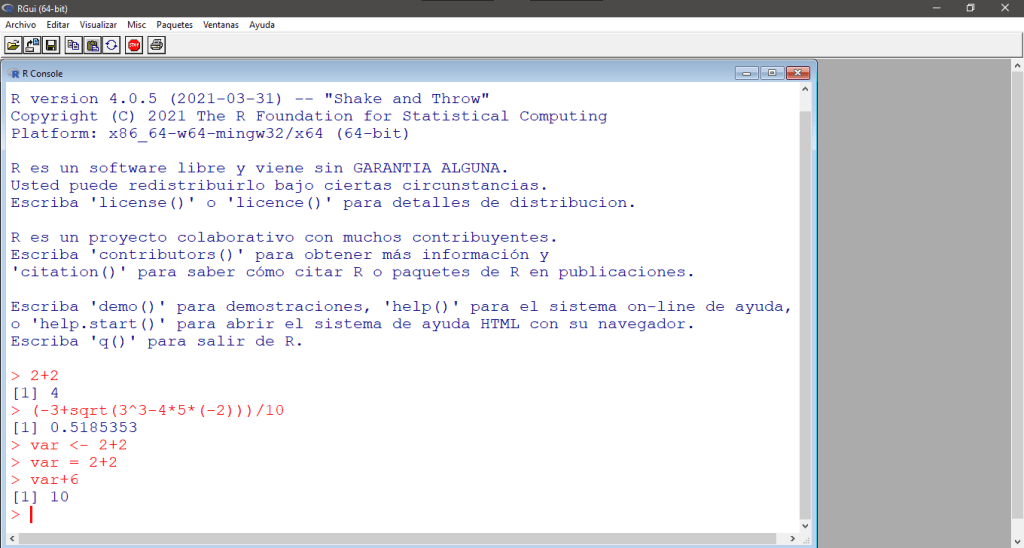
Podemos también definir otras variables y efectuar operaciones entre ellas. Por ejemplo, si definimos una variable var_1 que almacena el producto de tres por cinco y otra variable var_2 que almacena la división de doce entre cuatro, podemos efectuar la resta de estas dos variables.

Para esto, ejecutamos las siguientes instrucciones:

var_1 <- 3*5

var_2 <- 12/4

var_1 - var_2

Para ejecutar cada instrucción presionamos la tecla ENTER e inmediatamente debemos ver el resultado.

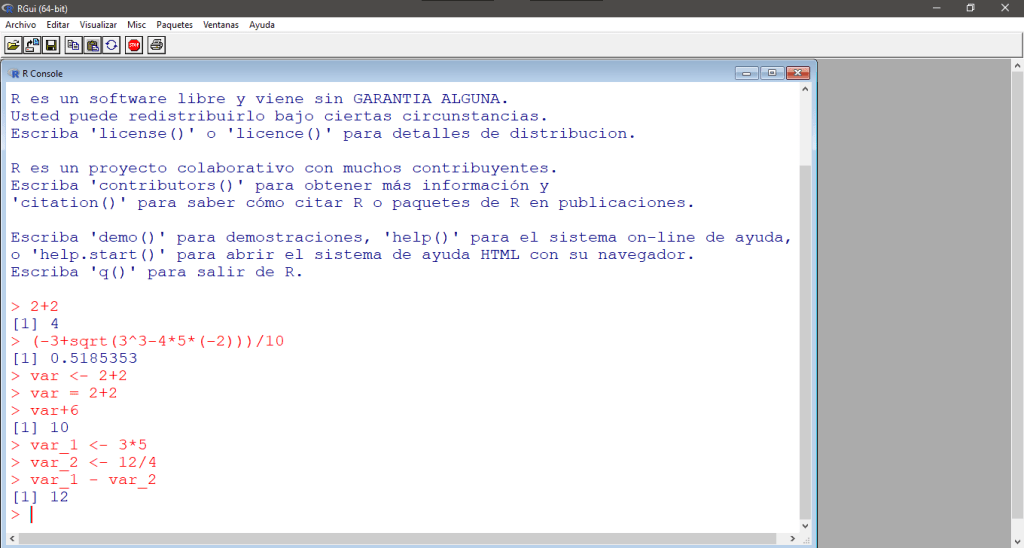
> var_1 <- 3*5
> var_2 <- 12/4
> var_1 - var_2
[1] 12

En su pantalla debería aparecer:

Scripts

Trabajar con problemas más complejos requiere de instrucciones más complejas, o incluso, secuencias de instrucciones. Afortunadamente, la interfaz gráfica de R trae incorporada un editor de texto que nos permite escribir estas secuencias de instrucciones y que además, se pueden ejecutar sin necesidad de copiarlas y pegarlas en la consola.

Un script es una secuencia de instrucciones que nos permite llevar a cabo una tarea, estos se escriben en el editor de texto que provee R para posteriormente ser ejecutados, ya sean línea por línea o en su totalidad. Para crear un nuevo script, ubicamos el menú de Archivo, hacemos click en él y seleccionamos Nuevo Script.

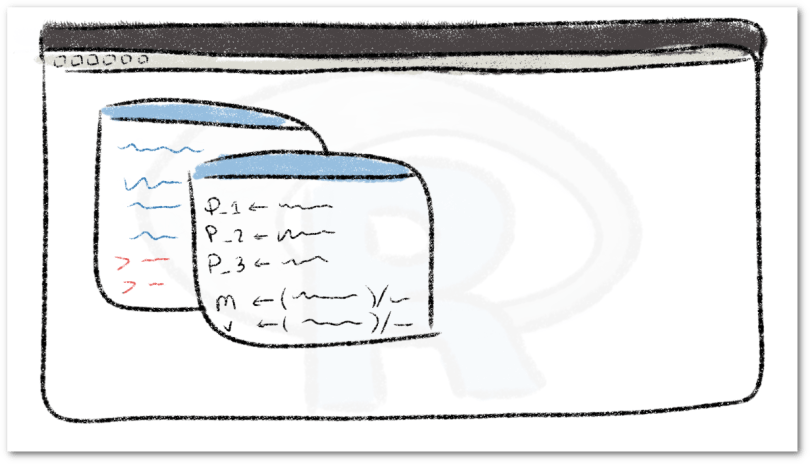
Inmediatamente se abrirá una nueva ventana con un editor de texto sobre el cuál podemos escribir.

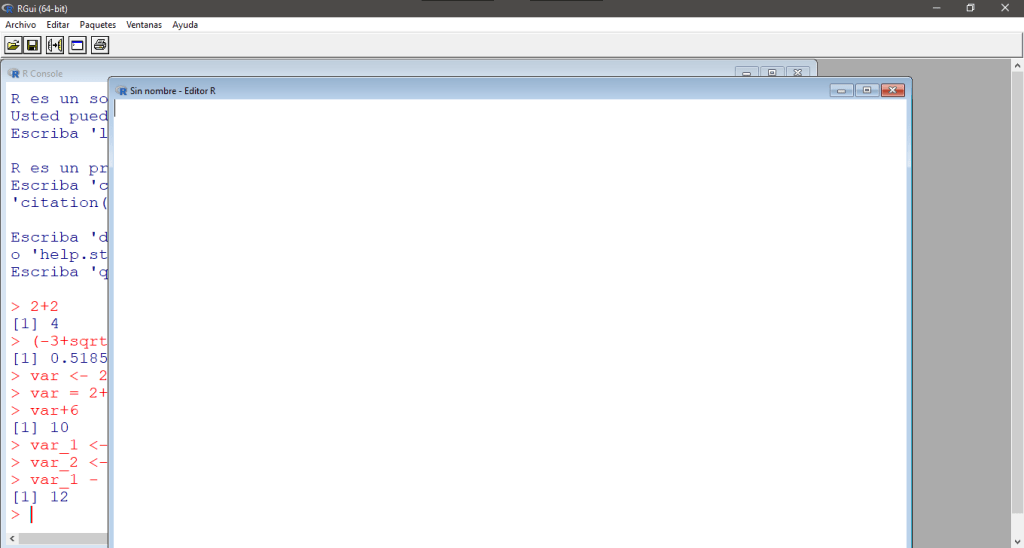
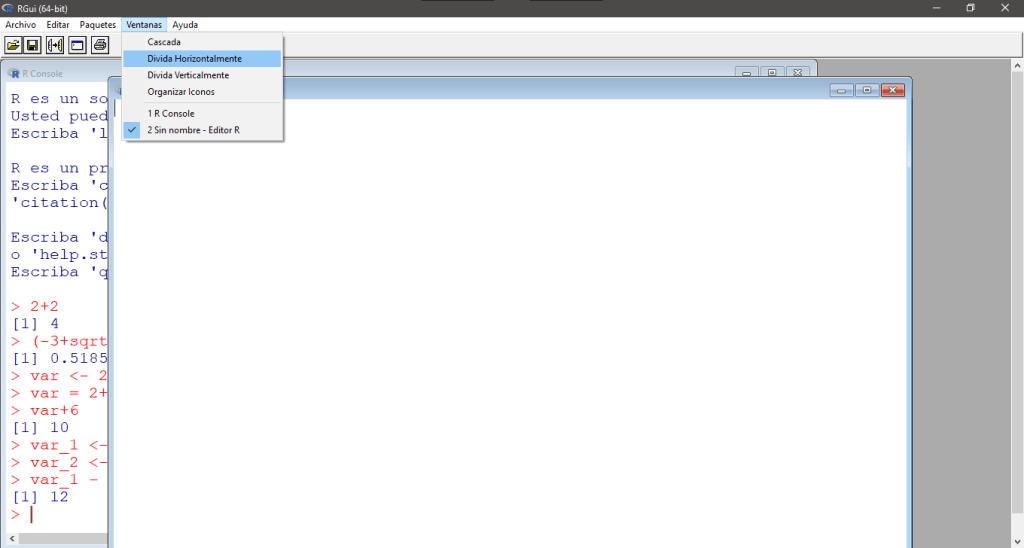
En este momento, recomiendo ajustar el tamaño y posición de la ventana que muestra la consola y la ventana que muestra el script para poder observar ambas con mayor comodidad, para esto, ubicamos el menú Ventanas, hacemos click en él y seleccionamos el arreglo más cómodo. A mí en particular me gusta la pantalla Dividida Horizontalmente.

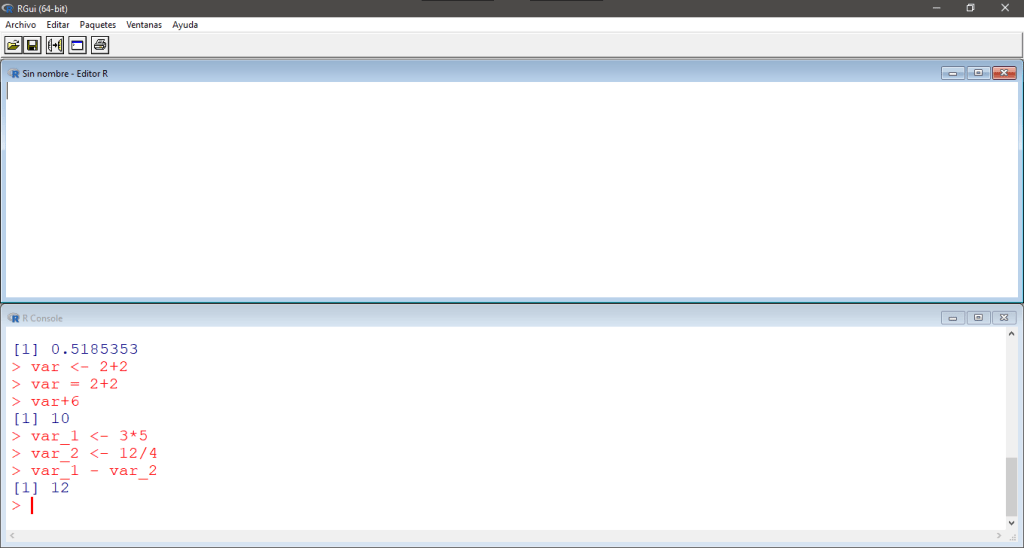
Veamos un ejemplo de un script simple.

Suponga que tiene la siguiente tarea: Considerando cinco personas, guarde las edades de cada uno en cinco variables distintas llamadas p_1, p_2, p_3, p_4 y p_5; calcule la edad promedio de estos y guarde este valor en una variable llamada m; calcule la varianza de este conjunto de datos y guarde este valor en una variable llamada var.

Los datos con los que contamos son los siguientes:

Juan tiene 52 años.
Pedro tiene 14 años.
Fabiana tiene 33 años.
Jerick tiene 5 años.
Laura tiene 23 años.

Definimos las variables escribiendo las siguientes instrucciones en nuestro script:

p_1 <- 52
p_2 <- 14
p_3 <- 33
p_4 <- 5
p_5 <- 23

La edad promedio de estas cinco personas, se calcula sumando todas las edades y dividiendo todo esto entre cinco, es decir,

$\dfrac{p_1 + p_2 + p_3 + p_4 + p_5}{5}$

Entonces, escribimos la siguiente instrucción en nuestro script:

m <- (p_1 + p_2 + p_3 + p_4 + p_5)/5

La varianza mide la variabilidad de los datos respecto a su media y se calcula sumando los cuadrados de la diferencias entre cada observación y la media, y dividiendo todo esto entre cinco, es decir,

$\dfrac{(p_1-m)^2 + (p_2 -m)^2 + (p_3 -m)^2 + (p_4 -m)^2 + (p_5 -m)^2 }{5}$

Entonces, escribimos la siguiente instrucción en nuestro script:

var <- ((p_1-m)^2 + (p_2 -m)^2  + (p_3 -m)^2  + (p_4 -m)^2  + (p_5 -m)^2)/5

En su pantalla debería aparecer:

Puede ejecutar la instrucción de cada línea en el script seleccionándola y haciendo click en el botón de correr línea o puede ejecutar todas las instrucciones de una vez seleccionando todas las líneas y presionando correr línea.

De esta forma, se ejecutan las instrucciones en la consola sin necesidad de copiarlas y pegarlas, además, el script se mantiene intacto, lo que permite manipular las instrucciones con facilidad en el caso que hayamos escrito algo mal.

En la consola aparecerá:

> p_1 <- 52
> p_2 <- 14
> p_3 <- 33
> p_4 <- 5
> p_5 <- 23
> m <- (p_1 + p_2 + p_3 + p_4 + p_5)/5
> var <- ((p_1-m)^2 + (p_2 -m)^2  + (p_3 -m)^2  + (p_4 -m)^2  + (p_5 -m)^2)/5

Ley de los Signos

18.03.202117.12.2022 Anthonny Arias-García3 comentarios

Al efectuar el producto entre números reales, debemos ser estar muy atentos al signo de los factores involucrados para llegar a la conclusión correcta. Es por esto que enunciaremos los cuatro casos que se pueden presentar al efectuar el producto de de dos factores.

También pudiera interesarte

Consideremos dos números reales $a$ y $b$ ; y para ser enfáticos, los denotaremos con $+a$ y $+b$ . En contraparte, consideremos sus opuestos aditivos denotados con $-a$ y $-b$ , entonces tenemos que:

$(+a) \cdot (+b) = +(a \cdot b)$

$(-a) \cdot (+b) = -(a \cdot b)$

$(+a) \cdot (-b) = -(a \cdot b)$

$(-a) \cdot (-b) = +(a \cdot b)$

De esta forma, podemos establecer una regla informal conocida como la Ley de Los Signos sobre el producto de números enteros de la siguiente forma:

Más por más, más.
Más por menos, menos.
Menos por más, menos.
Menos por menos, más.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ejemplo

Ejemplo 1

Para efectuar el producto $3 \cdot 3$ , el signo de ambos factores es positivo, así que los multiplicamos y el resultado tendrá signo positivo.

$3 \cdot 3 = 9$

Ejemplo 2

Para efectuar el producto $2 \cdot \sqrt(5)$ , el signo de ambos factores es positivo, así que los multiplicamos y el resultado tendrá signo positivo.

$2 \cdot \sqrt{5} = 2 \sqrt{5}$

Ejemplo 3

Para efectuar el producto $(-2) \cdot 5$ , el signo de ambos factores distinto, así que los multiplicamos y el resultado tendrá signo negativo.

$(-2) \cdot 5 = - ( 2 \cdot 5 ) = -10$

Ejemplo 4

Para efectuar el producto $(-3) \cdot \frac{1}{3}$ , el signo de ambos factores distinto, así que los multiplicamos y el resultado tendrá signo negativo.

$(-3) \cdot \frac{1}{3} = - ( 3 \cdot \frac{1}{3} ) = -1$

Ejemplo 5

Para efectuar el producto $6 \cdot (-3)$ , el signo de ambos factores distinto, así que los multiplicamos y el resultado tendrá signo negativo.

$6 \cdot (-3) = - (6 \cdot 3) = -18$

Ejemplo 6

Para efectuar el producto $10 \cdot (-\sqrt{7})$ , el signo de ambos factores distinto, así que los multiplicamos y el resultado tendrá signo negativo.

$10 \cdot (- \sqrt{7}) = - (10 \cdot \sqrt{7}) = -10 \sqrt{7}$

Ejemplo 7

Para efectuar el producto $(-4) \cdot (-8)$ , el signo de ambos factores es negativo, así que los multiplicamos y el resultado tendrá signo positivo.

$(-4) \cdot (-8) = (4 \cdot 8) = 32$

Ejemplo 8

Para efectuar el producto $(-x) \cdot (-x)$ , donde $x$ es una variable real. Notemos que si bien no sabemos si la variable es positiva o negativa, el signo de ambos factores es negativo, así que los multiplicamos y el resultado tendrá signo positivo.

$(-x) \cdot (-x) = (x \cdot x) = x^2$

Herramientas Básicas de una Calculadora Científica

17.10.202004.04.2024 Anthonny Arias-García2 comentarios

En mis años de experiencia docente a nivel universitario, he notado que si bien, la mayoría de los estudiantes tienen acceso a una calculadora científica, el uso que se le da no es mayor del que se le puede dar a una «calculadora bodeguera», es decir, una de este tipo

MX-12B | Serie con valor agregado | HOGAR | Calculadoras | CASIO

La Calculadora CASIO fx-82MS

La calculadora más común encontrada en las aulas de clases, desde bachillerato hasta el nivel universitario, es la calculadora CASIO fx-82MS. Aunque es sencilla en comparación con otras calculadoras científicas, es muy versátil.

Aparte de las operaciones de suma, resta, multiplicación y división. Veamos cuales son las operaciones básicas que se pueden efectuar con esta calculadora, pero además, veamos que con conocimientos matemáticos, varias de las opciones se pueden usar para hacer distintos tipos de operaciones.

Fracciones y Decimales

Las operaciones con fracciones o con decimales pueden resultar engorrosas para calcular a mano, afortunadamente, las calculadoras tienen una opción para reescribir fracciones como números decimales y viceversa. Para esto, se debe presionar el siguiente botón:

Este botón, reescribirá los números decimales como fracciones mixtas, particularmente para poder usar la opción correspondiente a las fracciones puras, se debe presionar la tecla SHITF previamente, pues con ella se pueden usar las opciones resaltadas en amarillo sobre cada tecla.

Potencias

El caso en el que más se usa una potencia en los cursos de matemáticas es cuando debemos elevar un número al cuadrado, seguido de esto, cuando debemos elevar un número al cubo. Para esto, existen dos botones dedicados.

Sin embargo, ¿qué haremos si queremos elevar un número a la 4? ¿O a la 10? ¿Y a la 7/5? Para esto, debemos usar el circunflejo… ¿El circunqué? El circunflejo es el signo (^) y de forma general, en el lenguaje matemático compucional, se usa para denotar una potencia.

Usando esta tecla, podemos calcular distintas potencias, de forma que

Si queremos calcular 6 elevado a la 4, entonces escribimos
6^4.
Si queremos calcular 2 elevado a la 10, entonces escribimos
2^10.
Si queremos calcular 4 elevado a la 7/5, entonces escribimos
4^(7/5).

Nótese que en este último caso, se usaron paréntesis para escribir la potencia. Esto es para indicarle a la calculadora que primero debe hacer las operación que está dentro del paréntesis. El uso de los paréntesis para definir operaciones es necesario para no incurrir en errores de cálculo.

Radicales

El caso en el que más se usa un radical en los cursos de matemáticas es cuando debemos calcular la raíz cuadrada, seguido de esto, cuando debemos calcular la raíz cúbica. Para esto, existen dos botones dedicados.

Particularmente para poder usar la opción correspondiente a la raíz cúbica, se debe presionar la tecla SHITF previamente, pues con ella se pueden usar las opciones resaltadas en amarillo sobre cada tecla.

Sin embargo, ¿qué haremos si queremos calcular la raíz cuarta? ¿O a la raíz décima? ¿Y a la sétima de un número elevado a la 5? Para esto, debemos usar presionar SHIFT seguido de el circunflejo (^), pues con esto activamos la expresión $\sqrt[x]{ \ }$ .

Usando esta tecla, podemos calcular distintas raíces, de forma que

Si queremos calcular la raíz cuarta de 6, entonces escribimos
4 $\sqrt[x]{ \ }$ 6.
Si queremos calcular la raíz décima de 2, entonces escribimos
10 $\sqrt[x]{ \ }$ 2.
Si queremos calcular la raíz quinta de 4 elevado a la 7, entonces escribimos
5 $\sqrt[x]{ \ }$ (4^7).

También nos podemos fijar que la raíz quinta de 4 elevado a la 7 también se puede calcular usando 4^(7/5), esto se debe a que de acuerdo a las propiedades de las potencias y radicales, tenemos que

$a^{\frac{m}{n}} = \sqrt[n]{a^m}$

Logaritmos

Los logaritmos se usan con frecuencia para estudiar cambios proporcionales o porcentuales en conjuntos de datos. Usualmente se considera el logaritmo con base 10 o el logarimo con base $\textit{\Large e}$ , este último conocido como el logaritmo neperiano o logaritmo natural. Para esto, existen dos botones dedicados.

Usando esta tecla, podemos calcular distintos logaritmos, de forma que

Si queremos el logaritmo base 10 de 6, entonces escribimos
log6.
Si queremos el logaritmo base 10 de 2 elevado a la 5, entonces escribimos
log(2^5).
Si queremos el logaritmo neperiano de 8, entonces escribimos
ln8.
Si queremos el logaritmo neperiano de la raíz cúbica de 15, entonces escribimos
ln( $\sqrt[3]{ \ }$ 15).

Calcular el logaritmo de cualquier base

Usualmente, las calculadoras científicas sólo permiten calcular el logaritmo base diez o el logaritmo neperiano. Sin embargo, debemos recordar la propiedad cambio de base, que indica que

$\log_a(b) = \dfrac{\log_c(b)}{\log_c(a)}$

Entonces, podemos calcular el logaritmo de cualquier base en la calculadora de la siguiente forma:

Si queremos el logaritmo base 3 de 2, entonces escribimos
log2/log3.
Si queremos el logaritmo base 9 de 13, entonces escribimos
log13/log9.
Si queremos el logaritmo base 12 de 33, entonces escribimos
log(33)/log12.
Si queremos el logaritmo base 5 de 4+7, entonces escribimos
log(4+7)/log5.

Exponenciales

Hay una potencia muy particular que debemos calcular con regularidad cuando se hacen desarrollos matemáticos y esta se presenta cuando operamos con la función exponencial. Usualmente se considera la base 10 o la base $\textit{\Large e}$ . Para esto, existen dos botones dedicados.

Para poder usar estas opciones, se debe presionar la tecla SHITF previamente, pues con ella se pueden usar las opciones resaltadas en amarillo sobre cada tecla.

Usando esta tecla, podemos calcular distintas expresiones exponciales, de forma que

Si queremos 10 elevado a la 6, entonces escribimos
$10^x$ 6.
Si queremos 10 elevado a la 2, entonces escribimos
$10^x$ 2.
Si queremos 10 elevado a la 7/3, entonces escribimos
$10^x$ (7/3).
Si queremos $\textit{\Large e}$ elevado a la 8, entonces escribimos
$\textit{\Large e}^x$ 8.
Si queremos $\textit{\Large e}$ elevado a la 15 + 5, entonces escribimos
$\textit{\Large e}^x$ (15+5).

Para definir directamente el número $\textit{\Large e}$ tenemos dos opciones, podemos escribir $\textit{\Large e}^x$ 1 o podemos presionar el siguiente botón

Para poder usar estas opciones, se debe presionar la tecla ALPHA previamente, pues con ella se pueden usar las opciones resaltadas en rojo sobre cada tecla.

Usando esta tecla, podemos calcular distintas expresiones exponciales con base $\textit{\Large e}$ , de forma que

Si queremos $\textit{\Large e}$ elevado a la 3, entonces escribimos
$\textit{\Large e}$ ^3.
Si queremos $\textit{\Large e}$ elevado a la 1/2, entonces escribimos
$\textit{\Large e}$ ^(1/2).

Guardar un número en la memoria de la calculadora

Al hacer recurrir varias veces un mismo cálculo, resulta engorroso tener que escribir la operación una y otra vez. Afortunadamente, las calculadoras cuentan una opción para guardar números o resultados de operaciones en una calculadora.

La opción STO denota la palabra en inglés storage, que se traduce como almacenamiento en español. La calculadora CASIO fx-82MS tiene seis espacios disponibles para almacenar en su memoria, estos son los correspondientes a A, B, C, D, E y F.

Almacenar un número en la memoria se efectúa en tres pasos sencillos. Supongamos que debe almacenar el número 3 en el espacio de memoria A. Entonces, debe presionar 3, seguido de STO (presionando previamente SHITF), seguido de la tecla correspondiente a A (sin presionar ALPHA):

Posteriormente, deberá aparecer en la pantalla lo siguiente:

3 $\rightarrow$ A

De esta forma, si hacemos el llamado de A (presionando previamente ALPHA), este tendrá almacenado el valor 3. Entonces, si escribimos

7 + A

El resultado será igual a 10, pues es como sumar 7+3.

Aunque no pareciera muy útil para operaciones sencillas, esto resultará de utilidad en el caso que estemos evaluando un polinomio. Supongamos que usted está calculando los máximos y mínimos del polinomio $P(x) = x^3 - 2x^2 -x +2$ y uno de sus puntos críticos es $x_1=\frac{2 + \sqrt{7}}{3}$ .

Para evalular el polinomio en esta expresión, lo más conveniente es guardarla en la memoria. Si queremos guardarla en el espacio B, seguimos los siguientes pasos

Escribimos la operación
(2 + $\sqrt{ \ }$ 7)/3
Seguido de STO (presionando previamente SHITF)
Seguido de B (sin presionar ALPHA)

Posteriormente, deberá aparecer en la pantalla lo siguiente:

(2 + $\sqrt{ \ }$ 7)/3 $\rightarrow$ B

Una vez que hemos almacenado este valor en memoria, podemos usarlo para evalular el polinomio en ese punto crítico, de la siguiente forma.

B^3 – 2B^2 -B +2

La Diferencia de Cuadrados

13.04.202007.12.2022 Anthonny Arias-García9 comentarios

Al efectuar operaciones matemáticas es común toparse con restas entre dos números, sin embargo, al encontrar la resta de los cuadrados de dos números diremos que esta es una diferencia de cuadrados y es de nuestro particular interés porque a través de la propiedad distributiva, podemos expresarla como el producto de dos factores.

También pudiera interesarte

Formalmente, si $a$ y $b$ son dos números reales, entonces la diferencia de sus cuadrados será igual a la suma del primero más el segundo, multiplicado por la resta del primero por el segundo, es decir,

La Diferencia de Cuadrados | totumat.com

Esta igualdad se puede deducir efectuando la propiedad distributiva de los números reales, veamos entonces,

Este tipo de expresiones se encuentra a menudo en el desarrollo las operaciones algebraicas y se usa principalmente para factorizar operaciones, veamos en los siguientes ejemplos como aplicar esta operación:

Anuncios

Ejemplos

Ejemplo 1

Factorice la expresión $5^2 - 3^2$ . Notamos que en este caso, podemos simplemente aplicar la potencia cada uno de los sumandos y efectuar la resta directamente.

$5^2 - 3^2 \ =\ 25 - 9$

$\ =\ 16$

Ejemplo 2

Factorice la expresión $x^2 - 9$ . Notamos que en este caso, uno de los sumandos es equis al cuadrado y el otro es nueve, así que no podemos efectuar la resta entre ellos así que aplicamos la diferencia de cuadrados notando que nueve es igual a tres al cuadrado.

$x^2 - 9 \ =\ x^2 - 3^2$

$\ =\ (x-3)(x+3)$

Ejemplo 3

Factorice la expresión $x^2 - 2$ . Notamos que en este caso, uno de los sumandos es equis al cuadrado y el otro es dos, así que no podemos efectuar la resta entre ellos así que aplicamos la diferencia de cuadrados notando que dos se puede reescribir como $2 = \left( \sqrt{2} \right)^2$ .

$x^2 - 2 \ =\ x^2 -\left( \sqrt{2} \right)^2$

$\ =\ \left(x-\sqrt{2}\right) \left(x+\sqrt{2}\right)$

De esta forma, podemos notar que si la raíz cuadrada de un numero no es exacta, este se puede reescribir para poder usar la diferencia de cuadrados.

Anuncios

Ejemplo 4

Factorice la expresión $8 - x^6$ . Notamos que en este caso, uno de los sumandos es 8 y el otro es equis a la seis, así que no podemos efectuar la resta entre ellos así que aplicamos la diferencia de cuadrados notando que ocho se puede reescribir como $8 = \left( \sqrt{8} \right)^2$ y equis a la seis como $x^6 = \left( x^3 \right)^2$ .

$8 - x^6 \ =\ \left( \sqrt{8} \right)^2 - \left(x^3 \right)^2$

$\ =\ \left(\sqrt{8}-x^3\right) \left(\sqrt{8}+x^3\right)$

Ejemplo 5

Factorice la expresión $36x^4 - 5x^8$ . Notamos que en este caso, no podemos efectuar la resta entre ellos así que aplicamos la diferencia de cuadrados usando las observaciones expuestas en los ejemplos anteriores.

$36x^4 - 5x^8 \ =\ \left( 6x^2 \right)^2 - \left( \sqrt{5}x^4 \right)^2$

$\ =\ \left(6x^2-\sqrt{5}x^4\right) \left(6x^2+\sqrt{5}x^4\right)$

La Propiedad Distributiva

13.04.202007.12.2022 Anthonny Arias-García6 comentarios

Al sumar números reales tenemos la libertad de asociar los números involucrados con ligereza y de igual forma, podemos asociar los números involucrados si estamos multiplicando números reales, sin embargo, debemos ser precavidos cuando nos topamos con operaciones mixtas, es decir, sumas y productos al mismo tiempo. A continuación veremos una propiedad que nos permite operar sumas y productos al mismo tiempo.

También pudiera interesarte

La propiedad distributiva establece que si un número multiplica a la suma de dos números, entonces el factor involucrado se distribuye entre cada uno de los sumandos. Formalmente, si $a$ , $b$ y $c$ son números reales, entonces

Podemos también aplicar esta propiedad si dentro de los paréntesis está involucrada una resta en vez de una suma, de la siguiente forma:

Notamos que si observamos esta igualdad de derecha a izquierda, estamos tomando el factor común que hay en ambos sumandos y lo estamos sacando a multiplicar:

$a \cdot b \pm a \cdot c = a \cdot (b \pm c)$

Esta es una de las propiedades más usadas en al cálculo de operaciones mixtas y a partir de ellas, se deducen algunos casos que facilitan la simplificación de expresiones matemáticas. Veamos algunos ejemplos para entender bien esta propiedad:

Anuncios

Ejemplos

Ejemplo 1

Use la propiedad distributiva para expandir la expresión $2 \cdot (1 + 6)$ . En este caso no es necesario usar la propiedad distributiva ya que podemos sumar los números que están dentro de los paréntesis y posteriormente multiplicar de la siguiente forma:

$2 \cdot (1 + 6) = 2 \cdot 7 = 14$

Ejemplo 2

Use la propiedad distributiva para expandir la expresión $2 \cdot \left( 1 + \sqrt{6} \right)$ . Notemos que uno de los sumandos involucrados es la raíz cuadrada de 6, por lo tanto no se puede sumar con 1, entonces distribuimos el factor involucrado

$2 \cdot \left( 1 + \sqrt{6} \right) = 2 \cdot 1 + 2 \cdot \sqrt{6} = 2 + 2 \sqrt{6}$

Ejemplo 3

Use la propiedad distributiva para expandir la expresión $5 \cdot \left( x - \sqrt{10} \right)$ . Notemos que uno de los sumandos involucrados es la raíz cuadrada de 10 y el otro es una incógnita, por lo tanto no se pueden restar, entonces distribuimos el factor involucrado

$5 \cdot \left( x - \sqrt{10} \right) = 5 \cdot x - 5 \cdot \sqrt{10} = 5x - 5\sqrt{10}$

Ejemplo 4

Use la propiedad distributiva para expandir la expresión $x \cdot \left( x + x^2 \right)$ . Notemos que uno de los sumandos involucrados una incógnita y el otro es una incógnita elevada al cuadrado, por lo tanto no se pueden sumar, entonces distribuimos el factor involucrado

$x \cdot \left( x + x^2 \right) = x \cdot x + x \cdot x^2 = x^2 + x^3$

Ejemplo 5

Use la propiedad distributiva para sacar el factor común de la expresión $18 + 3\sqrt{7}$ . Notemos que $18=3 \cdot 6$ , entonces,

$18 + 3\sqrt{7} = 3 \cdot 6 + 3 \sqrt{7} = 3 \cdot \left( 6 + \sqrt{7} \right)$

Ejemplo 6

Use la propiedad distributiva para sacar el factor común de la expresión $x^4 - 8x$ . Notemos que uno de los sumandos involucrados es una incógnita elevada a la cuatro y el otro es 8 veces dicha incógnita, por lo tanto no se pueden restar, entonces

$x^4 - 8x = x \cdot x^3 - x \cdot 8 = x \cdot \left( x^3 - 8 \right)$

Ejemplo 7

Use la propiedad distributiva para sacar el factor común de la expresión $12x^7 + 15x^4$ . Estos dos elementos no se pueden sumar, entonces

$12x^7 + 15x^4 = 3 \cdot 4 \cdot x^4 \cdot x^3 + 3 \cdot 5 \cdot x^4 = 3 x^4 \cdot \left( 4x^3 + 5 \right)$

Anuncios

Ejemplo 8

Use la propiedad distributiva para expandir la expresión $2 \cdot (3x + 4 + 7x + 5)$ . Notemos que podemos agrupar los elementos que están dentro de los paréntesis, para obtener

$2 \cdot (3x + 7x + 4 + 5)$

Sumamos los elementos que están multiplicando a $x$ y por otra parte, los términos independientes.

$2 \cdot (10x + 9)$

Finalmente, efectuamos la propiedad distributiva.

$20x + 18$

Ejemplo 9

Use la propiedad distributiva para expandir la expresión $5 \cdot (10 + x - 5x + 6y - 6 + 8y)$ . Notemos que podemos agrupar los elementos que están dentro de los paréntesis, para obtener

$5 \cdot (x - 5x + 6y +8y + 10 - 6)$

Sumamos los elementos que están multiplicando a $x$ , por otra parte los elementos que están multiplicando a $y$ y por otra parte, los términos independientes.

$5 \cdot (- 4x + 14y + 4)$

Finalmente, efectuamos la propiedad distributiva.

$-20x + 70y + 20$

Ejemplo 10

Use la propiedad distributiva para expandir la expresión $(\frac{24}{100}q + 10) \cdot q$ . Pese a que la variable $q$ aparece como un factor en el lado derecho de la expresión, podemos distribuirlo en cada uno de los sumandos tal como si apareciera del lado izquierdo:

$\frac{24}{100}q \cdot q + 10 \cdot q$

Notando que al multiplicar $q \cdot q$, ambos factores tienen la misma base, entonces obtenemos lo siguiente

$\frac{24}{100}q^2 + 10q$

La interfaz gráfica de R

Consola

Operaciones básicas

Variables

Scripts

Comparte

Ejemplo

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Ejemplo 5

Ejemplo 6

Ejemplo 7

Ejemplo 8

Comparte

La Calculadora CASIO fx-82MS

Fracciones y Decimales

Potencias

Radicales

Logaritmos

Calcular el logaritmo de cualquier base

Exponenciales

Guardar un número en la memoria de la calculadora

Comparte

Ejemplos

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Ejemplo 5

Comparte

Ejemplos

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Ejemplo 5

Ejemplo 6

Ejemplo 7

Ejemplo 8

Ejemplo 9

Ejemplo 10

Video Complementario

Comparte