- Definición
- Clasificación de las Ecuaciones Diferenciales
- Ejemplos
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
- Solución de una Ecuación Diferencial
- Ejemplos
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
- Ejemplo 4
- Problemas de Valor Inicial
- Teorema (de Existencia y Unicidad)
- Ejemplos
- Ejemplo 5
- Ejemplo 6
- Ejemplo 7
- Ejemplo 8
Definición
Definimos una ecuación diferencial como una expresión matemática que establece una relación entre una o más variables independientes; una o más variables dependientes; y las derivadas de estas variables dependientes a través de una igualdad.
También pudiera interesarte
Formalmente, considerando una variable independiente  y una variable que dependiente
y una variable que dependiente  , diremos que la siguiente expresión es una Ecuación Diferencial:
, diremos que la siguiente expresión es una Ecuación Diferencial:

De forma particular, si consideramos la siguiente relación

diremos que ésta es una ecuación diferencial.
Nuestro propósito será el de determinar qué función  es la que satisface esta igualdad y en este ejemplo, a simple vista podemos notar que
es la que satisface esta igualdad y en este ejemplo, a simple vista podemos notar que 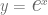 es una solución de esta ecuación diferencial pues
es una solución de esta ecuación diferencial pues  .
.
El estudio de las ecuaciones diferenciales tiene su base en el desarrollo de distintas técnicas para hallar la solución de distintas ecuaciones diferenciales y para esto debemos clasificarlas.
Clasificación de las Ecuaciones Diferenciales
Las ecuaciones diferenciales se clasifican de tres formas: Por tipo, por linealidad y por orden.
Por tipo: Si la ecuación diferencial involucra derivadas respecto a sólo una variable independiente, diremos que la ecuación diferencial es ordinaria. En otro caso, diremos que es una ecuación diferencial parcial.
Por linealidad: Una ecuación diferencial es lineal si ésta es lineal respecto a la variable dependiente y sus derivadas.
Por orden: El orden de una ecuación diferencial viene dada por la derivada de mayor orden que se encuentre involucrada en ésta.
A medida que aprendamos las técnicas para calcular soluciones de ecuaciones diferenciales, veremos otras formas de clasificarlas, por ahora consideremos algunos ejemplos de ecuaciones diferenciales para determinar la clasificación que hemos visto.
Ejemplos
Ejemplo 1
Si consideramos la ecuación diferencial  , entonces
, entonces
- Es ordinaria pues si consideramos
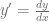 , notamos que ésta sólo involucra la derivada de sólo una variable independiente.
, notamos que ésta sólo involucra la derivada de sólo una variable independiente.
- Es lineal ya que el exponente de
 y
y  es exactamente igual a uno.
es exactamente igual a uno.
- Es de primer orden porque la derivada de mayor orden es de primer orden.
Por lo tanto es una Ecuación Diferencial Ordinaria lineal de primer orden.
Ejemplo 2
Si consideramos la ecuación diferencial  , entonces
, entonces
- Es ordinaria pues ésta sólo involucra una variable independiente.
- No es lineal ya que la variable dependiente
 está elevada al cubo.
está elevada al cubo.
- Es de tercer orden porque la derivada de mayor orden es de tercer orden.
Por lo tanto es una Ecuación Diferencial Ordinaria no lineal de tercer orden.
Ejemplo 3
Si consideramos la ecuación diferencial 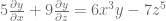 , entonces
, entonces
- Es parcial pues ésta involucra las derivadas respecto a más de una variable independiente.
- Es lineal ya que el exponente de
 ,
,  y
y  es exactamente igual a uno.
es exactamente igual a uno.
- Es de primer orden porque la derivada de mayor orden es de primer orden.
Por lo tanto es una Ecuación Diferencial Parcial lineal de primer orden.
Nota: Todas las ecuaciones diferenciales que consideraremos mientras estudiemos los aspectos básicos, serán Ecuaciones Diferenciales Ordinarias, es por esto que siempre consideraremos 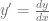 , salvo que se indique otra variable dependiente u otra variable independiente.
, salvo que se indique otra variable dependiente u otra variable independiente.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Solución de una Ecuación Diferencial
Si consideramos la ecuación diferencial

Diremos que una función 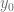 definida en un intervalo
definida en un intervalo  con
con  derivadas continuas en el intervalo
derivadas continuas en el intervalo  es la solución de esta ecuación diferencial de
es la solución de esta ecuación diferencial de  -ésimo orden, si esta satisface la igualdad planteada, es decir, tal que
-ésimo orden, si esta satisface la igualdad planteada, es decir, tal que

Consideremos algunos ejemplos para que ilustrar esta idea con mayor claridad.
Ejemplos
Ejemplo 1
Si consideramos la ecuación diferencial ordinaria 
La función  es una solución de esta ecuación diferencial, pues
es una solución de esta ecuación diferencial, pues

Diremos que esta es una solución particular pues debemos notar que 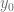 no es la única solución, si consideramos
no es la única solución, si consideramos  , esta también es una solución particular, ya que
, esta también es una solución particular, ya que

De forma general, si consideramos  para cualquier constante real
para cualquier constante real 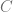 diremos que este tipo de solución es una solución general de la ecuación diferencial.
diremos que este tipo de solución es una solución general de la ecuación diferencial.
Ejemplo 2
Si consideramos la ecuación diferencial ordinaria 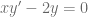
La función  es una solución de esta ecuación diferencial, pues
es una solución de esta ecuación diferencial, pues

Diremos que esta es una solución particular pues debemos notar que 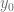 no es la única solución, si consideramos
no es la única solución, si consideramos , esta también es una solución particular, ya que
, esta también es una solución particular, ya que

De forma general, si consideramos  para cualquier constante real
para cualquier constante real 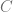 diremos que esta es la solución general de la ecuación diferencial.
diremos que esta es la solución general de la ecuación diferencial.
Ejemplo 3
Si consideramos la ecuación diferencial ordinaria  .
.
La función  es una solución de esta ecuación diferencial, pues
es una solución de esta ecuación diferencial, pues

Diremos que esta es una solución particular pues debemos notar que 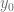 no es la única solución, si consideramos
no es la única solución, si consideramos  , esta también es una solución particular, ya que
, esta también es una solución particular, ya que

De forma general, si consideramos 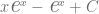 para cualquier constante real
para cualquier constante real 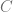 diremos que esta es la solución general de la ecuación diferencial.
diremos que esta es la solución general de la ecuación diferencial.
Ejemplo 4
Si consideramos la ecuación diferencial ordinaria 
La función  es una solución de esta, pues
es una solución de esta, pues

Diremos que esta es una solución particular pues debemos notar que la pena notar que 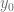 no es la única solución, si consideramos
no es la única solución, si consideramos 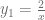 , esta también es una solución particular, ya que
, esta también es una solución particular, ya que

De forma general, si consideramos  para cualquier constante real
para cualquier constante real 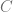 diremos que esta es la solución general de la ecuación diferencial.
diremos que esta es la solución general de la ecuación diferencial.
Tomando en cuenta los ejemplos expuestos, las soluciones de los primeros ejemplos están definidas para todos los números reales, sin embargo, esto no ocurre al considerar las soluciones de  pues particularmente, la función
pues particularmente, la función  no está definida cuando
no está definida cuando  . En este último caso, los intervalos
. En este último caso, los intervalos 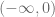 y
y  son los intervalos más grandes donde la solución está definida.
son los intervalos más grandes donde la solución está definida.
Entonces, es importante mencionar que al calcular la solución de una ecuación diferencial, por definición, esta debe estar definida en intervalos, es por esto que siempre consideraremos el mayor intervalo donde la solución y sus derivadas están definidas.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Problemas de Valor Inicial
Hay ecuaciones diferenciales cuya solución está condicionada sobre un punto, este tipo de condiciones es llamado problemas de condición inicial. Formalmente, diremos que la ecuación diferencial tiene un problema de valor inicial si la solución debe cumplir con la condición 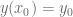 . Sin embargo, ¿cómo sabemos que en efecto podemos encontrar la solución de una ecuación que cumpla con esa condición? A continuación veremos un teorema que nos permitirá determinar si una ecuación diferencial con un problema de valor inicial tiene solución.
. Sin embargo, ¿cómo sabemos que en efecto podemos encontrar la solución de una ecuación que cumpla con esa condición? A continuación veremos un teorema que nos permitirá determinar si una ecuación diferencial con un problema de valor inicial tiene solución.
Teorema (de Existencia y Unicidad)
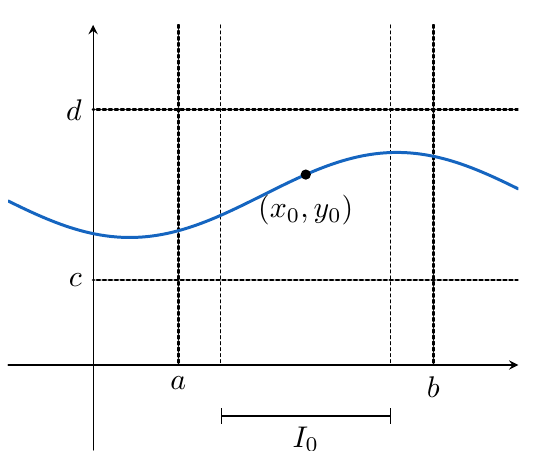
Considerando una ecuación diferencial de la forma  y
y 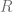 una región rectangular en el plano
una región rectangular en el plano  que contiene al punto
que contiene al punto 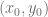 en su interior, definida por
en su interior, definida por

Si  y
y  son funciones continuas en la región
son funciones continuas en la región 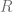 , entonces existe un intervalo
, entonces existe un intervalo  centrado en
centrado en 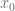 contenido en
contenido en ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) y una única función
y una única función  , definida en el intervalo
, definida en el intervalo  que es solución del problema de valor inicial
que es solución del problema de valor inicial 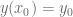 .
.
Las ecuaciones diferenciales que consideraremos de aquí en adelante cumplirán con las condiciones del Teorema de Existencia y Unicidad salvo que se diga lo contrario, sin embargo, siempre es importante verificar que se cumplan las condiciones antes de empezar a calcular la solución de una ecuación diferencial.
Ejemplos
Ejemplo 5
Si consideramos la ecuación diferencial ordinaria  con problema de valor inicial
con problema de valor inicial 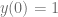 , esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues
, esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues
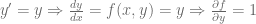
Así,  y
y  son funciones continuas en cualquier región
son funciones continuas en cualquier región 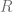 del plano
del plano  , existe un intervalo
, existe un intervalo  centrado en
centrado en  y una única función
y una única función  , definida en el intervalo
, definida en el intervalo  que es solución de la ecuación diferencial con problema de valor inicial
que es solución de la ecuación diferencial con problema de valor inicial 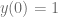 .
.
Particularmente la función 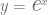 es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues
es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues

Ejemplo 6
Si consideramos la ecuación diferencial ordinaria 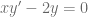 con problema de valor inicial
con problema de valor inicial 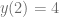 , esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues
, esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues

Así, considerando que  ,
,  y
y  son funciones continuas en cualquier región
son funciones continuas en cualquier región 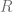 del plano
del plano  tal que
tal que  (
( ), existe un intervalo
), existe un intervalo  centrado en
centrado en  y una única función
y una única función  , definida en el intervalo
, definida en el intervalo  que es solución de la ecuación diferencial con problema de valor inicial
que es solución de la ecuación diferencial con problema de valor inicial  .
.
Particularmente la función  es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues
es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 7
Si consideramos la ecuación diferencial ordinaria  con problema de valor inicial
con problema de valor inicial  , esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues
, esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues

Así,  y
y  son funciones continuas en cualquier región
son funciones continuas en cualquier región 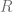 del plano
del plano  , existe un intervalo
, existe un intervalo  centrado en
centrado en 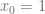 y una única función
y una única función  , definida en el intervalo
, definida en el intervalo  que es solución de la ecuación diferencial con problema de valor inicial
que es solución de la ecuación diferencial con problema de valor inicial  .
.
Particularmente la función  es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues
es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues
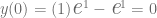
Ejemplo 8
Si consideramos la ecuación diferencial ordinaria  con problema de valor inicial
con problema de valor inicial 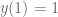 , esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues
, esta ecuación cumple con las condiciones del teorema de existencia y unicidad, pues

Así, considerando que  ,
,  y
y  son funciones continuas en cualquier región
son funciones continuas en cualquier región 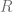 del plano
del plano  tal que
tal que  (
(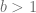 ), existe un intervalo
), existe un intervalo  centrado en
centrado en 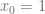 y una única función
y una única función  , definida en el intervalo
, definida en el intervalo  que es solución de la ecuación diferencial con problema de valor inicial
que es solución de la ecuación diferencial con problema de valor inicial  .
.
Particularmente la función  es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues
es una solución de esta ecuación diferencial que satisface la condición dada por el valor inicial, pues
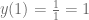
es una ecuación diferencial ordinaria lineal de primer orden no-homogénea y la solución de este tipo de ecuaciones se puede calcular usando el factor integrante.
, se puede reescribir como una ecuación diferencial ordinaria lineal de primer orden homogénea
y en consecuencia se puede calcular su solución separando las variables.
, diremos que una Ecuación de Bernoulli es una ecuación diferencial ordinaria no lineal expresada de la siguiente forma
y
fueron los nombrados en la introducción de esta sección. Así que veremos a continuación, el caso en el que
. Podemos calcular la solución de este tipo de ecuaciones usando recurriendo a la variable auxiliar
para obtener
que en este caso,
, por lo tango estará expresada como
de donde podemos despejar
elevando a
y de forma general, para hacer este despeje, se eleva a
ambos lados de la ecuación para obtener que
, así que usando la regla de la cadena concluimos que
y
en la ecuación diferencial
y así, reescribimos la nueva ecuación como una ecuación diferencial ordinaria lineal no-homogénea
que nos permite calcular el factor integrante de la siguiente manera
en función de
, volvemos a sustituirla para obtener

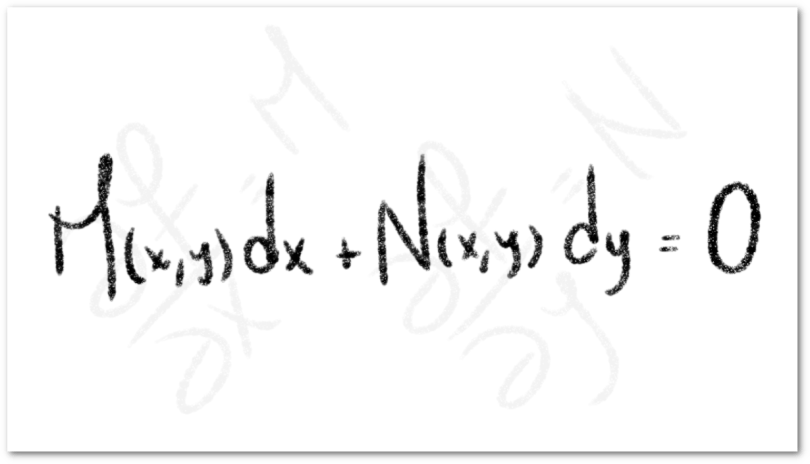
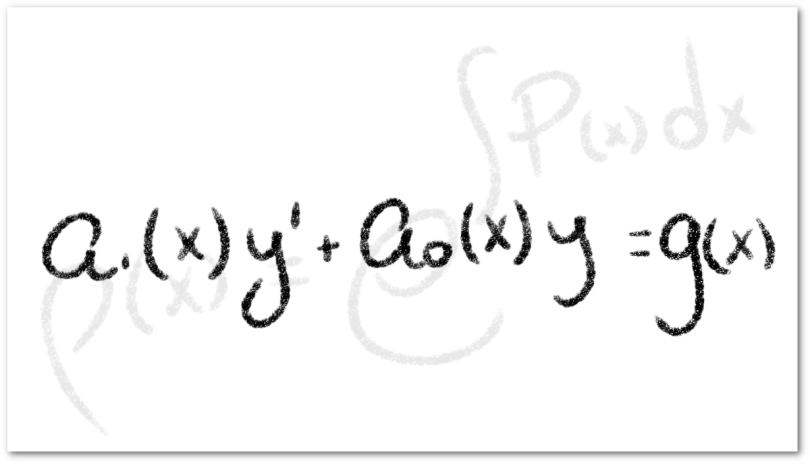
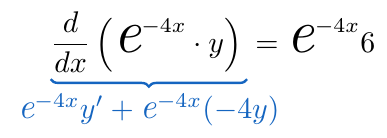
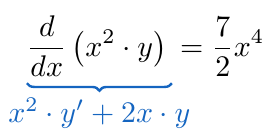
Debe estar conectado para enviar un comentario.