- Determinar la fórmula general de depreciación porcentual
- Ejemplos
- Ejemplo 5
- Ejemplo 6
- Ejemplo 7
- Ejemplo 8
- El valor de desecho
- Ejemplos
- Ejemplo 9
- Ejemplo 10
- Ejemplo 11
- Ejemplo 12
Al estudiar la depreciación simple, hemos visto como un bien pierde su valor describiéndolo de forma lineal, es decir, cuando su valor ser pierde de forma constante a través del tiempo, sin embargo, este no siempre será el caso, pues en ocasiones el valor de un bien se pierde dependiendo de las condiciones que se encuentre actualmente.
También pudiera interesarte
Digamos que este bien se adquiere en  y que este se deprecia en un
y que este se deprecia en un  por ciento cada cierto periodo de tiempo. Entonces, tenemos que
por ciento cada cierto periodo de tiempo. Entonces, tenemos que
Durante el transcurso del primer periodo, este bien tiene un valor de
Durante el transcurso del segundo periodo, este bien ha perdido un  por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de
por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de  y una vez que hemos sacado
y una vez que hemos sacado 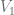 como un factor común, obtenemos
como un factor común, obtenemos
Durante el transcurso del tercer periodo, este bien ha perdido un  por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de
por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de 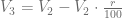 y una vez que hemos sacado
y una vez que hemos sacado  como un factor común, obtenemos
como un factor común, obtenemos
Durante el transcurso del cuarto periodo, este bien ha perdido un  por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de
por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de  y una vez que hemos sacado
y una vez que hemos sacado  como un factor común, obtenemos
como un factor común, obtenemos
Durante el transcurso del n-ésimo periodo, este bien ha perdido un  por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de
por cierto el valor que tenía en el periodo anterior, es decir, durante este periodo su valor es de  y una vez que hemos sacado
y una vez que hemos sacado  como un factor común, obtenemos
como un factor común, obtenemos
De esta forma, tenemos que en el n-ésimo periodo, el valor del bien está dado por

Notando entonces que el valor de este bien durante el transcurso del  -ésimo periodo está determinado por una sucesión geométrica decreciente, a esta expresión se le conoce como la fórmula de depreciación porcentual, al valor
-ésimo periodo está determinado por una sucesión geométrica decreciente, a esta expresión se le conoce como la fórmula de depreciación porcentual, al valor  se le conoce como valor inicial y a
se le conoce como valor inicial y a  se le conoce como la tasa porcentual de depreciación. Veamos entonces algunos ejemplos donde podemos aplicar esta fórmula.
se le conoce como la tasa porcentual de depreciación. Veamos entonces algunos ejemplos donde podemos aplicar esta fórmula.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 1
Suponga que una carnicería adquiere una moledora de carne con un valor de 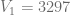 Ps. y esta se deprecia en un
Ps. y esta se deprecia en un  por ciento anual. Determine su valor en el año 4.
por ciento anual. Determine su valor en el año 4.
Nota: Perolitos (Ps.) es la moneda oficial de totumat.
Aplicando la fórmula, el valor de este bien viene dado de la siguiente manera:
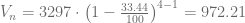
Por lo tanto, el valor de este bien en el año 4 es de 972.21 Ps.
Ejemplo 2
Suponga que una panificadora adquiere una amasadora con un valor de  Ps. y esta se deprecia en un
Ps. y esta se deprecia en un  por ciento anual. Determine su valor en el año 10.
por ciento anual. Determine su valor en el año 10.
Aplicando la fórmula, el valor de este bien viene dado de la siguiente manera:

Por lo tanto, el valor de este bien en el año 10 es de 6116.2 Ps.
Ejemplo 3
Suponga que una empresa constructora adquiere una batidora de cemento con un valor de  Ps. y esta se deprecia en un
Ps. y esta se deprecia en un  por ciento anual. Determine su valor en el año 8.
por ciento anual. Determine su valor en el año 8.
Aplicando la fórmula, el valor de este bien viene dado de la siguiente manera:

Por lo tanto, el valor de este bien en el año 8 es de 145.06 Ps.
Ejemplo 4
Suponga que una cafetería adquiere una máquina de espresso con un valor de 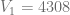 Ps. y esta se deprecia en un
Ps. y esta se deprecia en un  por ciento anual. Determine su valor en el año 2.
por ciento anual. Determine su valor en el año 2.
Aplicando la fórmula, el valor de este bien viene dado de la siguiente manera:

Por lo tanto, el valor de este bien en el año 2 es de 3092.84 Ps.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Considerando que la fórmula depreciación porcentual está determinada por una sucesión geométrica, es posible determinar la fórmula general de depreciación conociendo el valor que tuvo el bien en dos años distintos.
Formalmente, si consideramos el valor que el bien adquirió en dos años distintos, digamos  y
y  , podemos determinar el valor de
, podemos determinar el valor de  y de
y de  calculando la solución del siguiente sistema de ecuaciones:
calculando la solución del siguiente sistema de ecuaciones:
Veamos en los siguientes ejemplos como determinar la fórmula general de depreciación porcentual usando esta técnica.
Ejemplos
Ejemplo 5
Considerando que una moledora de carne tuvo un valor de 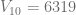 en el año 10 y
en el año 10 y  en el año 13 . Determine la fórmula general de depreciación porcentual de este bien.
en el año 13 . Determine la fórmula general de depreciación porcentual de este bien.
Para esto, calculamos la solución del siguiente sistema de ecuaciones:
Para calcular la solución de este sistema de ecuaciones dividimos ambas ecuaciones, notando que  para obtener la siguiente ecuación
para obtener la siguiente ecuación

A partir de esta ecuación podemos despejar  y para esto, elevamos ambos lados de la ecuación a la potencia
y para esto, elevamos ambos lados de la ecuación a la potencia  para obtener que
para obtener que
Una vez calculado  , podemos sustituir
, podemos sustituir  en la ecuación de nuestra preferencia para calcular
en la ecuación de nuestra preferencia para calcular  . Particularmente sustituimos
. Particularmente sustituimos  en la primera ecuación y despejamos
en la primera ecuación y despejamos 
Finalmente, el valor inicial del bien es  y la tasa porcentual de depreciación es de
y la tasa porcentual de depreciación es de  por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:
por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:
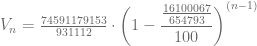
Ejemplo 6
Considerando que una amasadora tuvo un valor de 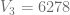 en el año 3 y
en el año 3 y 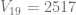 en el año 19 . Determine la fórmula general de depreciación porcentual de este bien.
en el año 19 . Determine la fórmula general de depreciación porcentual de este bien.
Para esto, calculamos la solución del siguiente sistema de ecuaciones:
Para calcular la solución de este sistema de ecuaciones dividimos ambas ecuaciones, notando que  para obtener la siguiente ecuación
para obtener la siguiente ecuación

A partir de esta ecuación podemos despejar  y para esto, elevamos ambos lados de la ecuación a la potencia
y para esto, elevamos ambos lados de la ecuación a la potencia  para obtener que
para obtener que
Una vez calculado  , podemos sustituir
, podemos sustituir  en la ecuación de nuestra preferencia para calcular
en la ecuación de nuestra preferencia para calcular  . Particularmente sustituimos
. Particularmente sustituimos  en la primera ecuación y despejamos
en la primera ecuación y despejamos 
Finalmente, el valor inicial del bien es 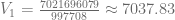 y la tasa porcentual de depreciación es de
y la tasa porcentual de depreciación es de 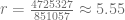 por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:
por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 7
Considerando que una batidora de cemento tuvo un valor de  en el año 2 y
en el año 2 y  en el año 3 . Determine la fórmula general de depreciación porcentual de este bien.
en el año 3 . Determine la fórmula general de depreciación porcentual de este bien.
Para esto, calculamos la solución del siguiente sistema de ecuaciones:
Para calcular la solución de este sistema de ecuaciones dividimos ambas ecuaciones, notando que  para obtener la siguiente ecuación
para obtener la siguiente ecuación

A partir de esta ecuación podemos despejar  y para esto, elevamos ambos lados de la ecuación a la potencia
y para esto, elevamos ambos lados de la ecuación a la potencia  para obtener que
para obtener que
Una vez calculado  , podemos sustituir
, podemos sustituir  en la ecuación de nuestra preferencia para calcular
en la ecuación de nuestra preferencia para calcular  . Particularmente sustituimos
. Particularmente sustituimos  en la primera ecuación y despejamos
en la primera ecuación y despejamos 
Finalmente, el valor inicial del bien es  y la tasa porcentual de depreciación es de
y la tasa porcentual de depreciación es de  por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:
por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:

Ejemplo 8
Considerando que una máquina de espresso tuvo un valor de  en el año 1 y
en el año 1 y 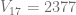 en el año 17 . Determine la fórmula general de depreciación porcentual de este bien.
en el año 17 . Determine la fórmula general de depreciación porcentual de este bien.
Para esto, calculamos la solución del siguiente sistema de ecuaciones:
Para calcular la solución de este sistema de ecuaciones dividimos ambas ecuaciones, notando que  para obtener la siguiente ecuación
para obtener la siguiente ecuación

A partir de esta ecuación podemos despejar  y para esto, elevamos ambos lados de la ecuación a la potencia
y para esto, elevamos ambos lados de la ecuación a la potencia  para obtener que
para obtener que
Una vez calcculado  , podemos sustituir
, podemos sustituir  en la ecuación de nuestra preferencia para calcular
en la ecuación de nuestra preferencia para calcular  . Particularmente sustituimos
. Particularmente sustituimos  en la primera ecuación y despejamos
en la primera ecuación y despejamos 
Finalmente, el valor inicial del bien es  y la tasa porcentual de depreciación es de
y la tasa porcentual de depreciación es de  por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:
por ciento. Entonces podemos expresar la fórmula general que define el valor de este bien de la siguiente manera:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
El valor de desecho
A medida que un bien pierde su valor, llega un punto en el que entrará en desuso o que su reventa no presentará un ingreso significativo, a este valor se le conoce como valor de desecho (o valor residual) y los años que pasan desde que se adquiere el bien hasta que su valor es igual al valor de desecho, se conoce como vida útil del bien.
Veamos en los siguientes ejemplos como calcular la vida útil de un bien considerando que su depreciación ha sido porcentual.
Ejemplos
Ejemplo 9
Suponga que una carnicería adquiere una moledora de carne con un valor de  Ps. y esta se deprecia en
Ps. y esta se deprecia en  por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 4190 .
por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 4190 .
Aplicando la fórmula de depreciación, el valor de este bien durante el  -ésimo año viene dado de la siguiente manera:
-ésimo año viene dado de la siguiente manera:

Nuestro propósito es determinar el valor de  para el cual
para el cual  , es decir, para el cual
, es decir, para el cual  y para esto, despejamos
y para esto, despejamos  .
.
Por lo tanto, la moledora de carne tiene una vida útil de aproximadamente 10 años.
Ejemplo 10
Suponga que una panificadora adquiere una amasadora con un valor de 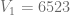 Ps. y esta se deprecia en
Ps. y esta se deprecia en  por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 815.
por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 815.
Aplicando la fórmula de depreciación, el valor de este bien durante el  -ésimo año viene dado de la siguiente manera:
-ésimo año viene dado de la siguiente manera:

Nuestro propósito es determinar el valor de  para el cual
para el cual  , es decir, para el cual
, es decir, para el cual  y para esto, despejamos
y para esto, despejamos  .
.
Por lo tanto, la amasadora tiene una vida útil de aproximadamente 11 años.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 11
Suponga que una empresa constructora adquiere una batidora de cemento con un valor de  Ps. y esta se deprecia en
Ps. y esta se deprecia en 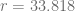 por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 3097.
por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 3097.
Aplicando la fórmula de depreciación, el valor de este bien durante el  -ésimo año viene dado de la siguiente manera:
-ésimo año viene dado de la siguiente manera:

Nuestro propósito es determinar el valor de  para el cual
para el cual  , es decir, para el cual
, es decir, para el cual 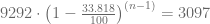 y para esto, despejamos
y para esto, despejamos  .
.
Por lo tanto, la batidora de cemento tiene una vida útil de aproximadamente 4 años.
Ejemplo 12
Suponga que una cafetería adquiere una máquina de espresso con un valor de  Ps. y esta se deprecia en
Ps. y esta se deprecia en 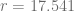 por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 2060.
por ciento anualmente. Determine su vida útil si su valor de desecho es igual a 2060.
Aplicando la fórmula de depreciación, el valor de este bien durante el  -ésimo año viene dado de la siguiente manera:
-ésimo año viene dado de la siguiente manera:

Nuestro propósito es determinar el valor de  para el cual
para el cual 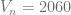 , es decir, para el cual
, es decir, para el cual  y para esto, despejamos
y para esto, despejamos  .
.
Por lo tanto, la máquina de espresso tiene una vida útil de aproximadamente 7 años.
y
son funciones que dependen de la variable
.
: el caso homogéneo con coeficiente constante, es decir, tal que
y
. En este caso, las ecuaciones estarán expresadas de la forma
. En este caso la constante
será conocida como constante de proporcionalidad y este tipo de ecuaciones sirve para describir diversos fenómenos de crecimiento y decrecimiento.
para denotar el tamaño de la población en un tiempo
, la forma en que varía el tamaño de la población respecto al tiempo se puede describir calculando la derivada de la variable
respecto al tiempo
, es decir,
.
es proporcional al tamaño de la población en dicho tiempo
, de esta forma, obtenemos la siguiente igualdad
. Y sabiendo el tamaño de la población en un punto
entonces podemos definir una ecuación diferencial con problema de valor inicial de la siguiente forma:
. Sin embargo, para agilizar los cálculos, podemos considerar
y así,
.
, entonces
. Para esto, debemos recurrir a la otra información aportada en el enunciado del problema.
y así,
. De esta forma, podemos plantear la siguiente igualdad
.
. Entonces, evaluamos la función en 60.










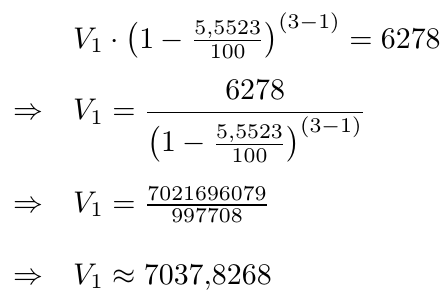





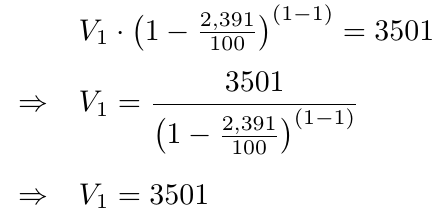





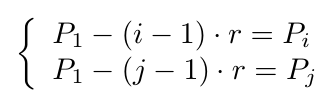

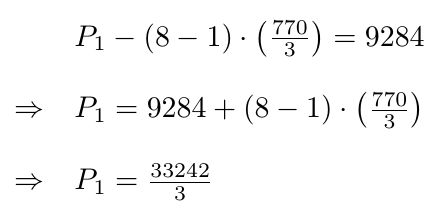












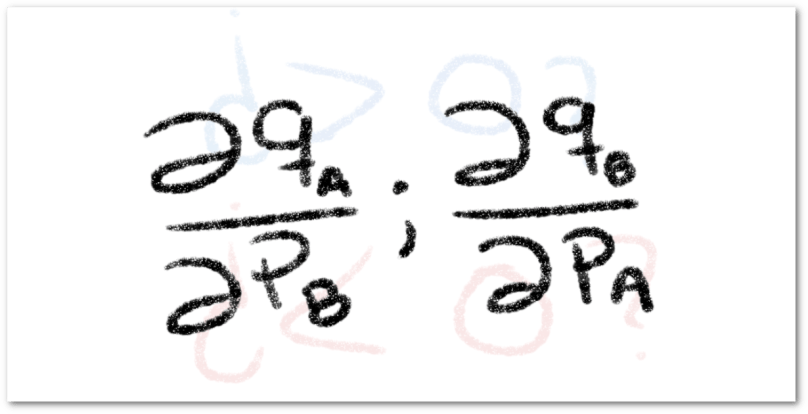
Debe estar conectado para enviar un comentario.