Incógnitas y Variables
¿Qué es una variable?
Si consideramos una ecuación, digamos , definimos una incógnita
como un número desconocido cuyo valor debemos calcular. Este valor está condicionado a la relación que establece la igualdad y que, una vez que aplicamos las técnicas de despeje, concluimos que
.
Sin embargo, el uso de puede extenderse, pues podemos usarla como un elemento cuyo valor puede variar. Si consideramos la expresión
, notamos inmediatamente que el valor de
no está restringido por una igualdad, así que esta pudiera tomar cualquier valor, por ejemplo,
- Si el valor de
es igual a
, entonces
.
- Si el valor de
es igual a
, entonces
.
- Si el valor de
es igual a
, entonces
.
De esta forma, si el valor de no tiene condiciones que lo fijen a un solo valor, podemos decir que este tiene un valor variable. Formalmente, decimos que una variable es un elemento que puede tomar cualquier valor en un conjunto dado y que usualmente se denota con
,
o
.
También pudiera interesarte
Potencias de la variable
Notemos que al considerar ecuaciones cuadráticas, éstas difieren de las ecuaciones lineales porque encontramos que la incógnita aparece multiplicada por ella misma, es decir, aparece
como un sumando.
Recordando que una potencia de un número real es el producto de dicho número
por sí mismo una cierta cantidad de veces, si multiplicamos
n veces, expresamos este producto con
y decimos que es la n-ésima potencia de
. A
lo llamamos exponente y a
lo llamamos base.
Estudiaremos en esta sección, una herramienta que nos define expresiones matemáticas que involucran potencias de una variable.
¿Qué es un polinomio?
Si decimos que x es un número real que puede adquirir cualquier valor en el conjunto de los números reales, entonces decimos que ésta es una variable real y si consideramos un conjunto de
números reales. Definimos un polinomio
con la siguiente expresión:
Considerando la expresión que define a un polinomio, podemos identificar varios elementos en ella:
- Al conjunto de números reales
los llamaremos coeficientes del polinomio.
- El coeficiente
será el coeficiente principal y es quien multiplica a la
con la mayor potencia.
- El coeficiente
será el término independiente y no multiplica la variable
, ni a sus potencias,
- Al número natural
lo llamaremos grado del polinomio y será el mayor de los exponentes involucrados en la expresión.
A un polinomio de grado dos, lo llamaremos polinomio cuadrático y a un polinomio de grado tres lo llamaremos polinomio cúbico.
Pareciera engorrosa la definición de lo que es un polinomio, pero con varios ejemplos veremos que son simplemente la suma de potencias de x multiplicadas por números reales.
Ejemplos
Ejemplo 1
Si consideramos el polinomio , podemos identificar en él los siguientes elementos:
- El grado es
- El coeficiente principal es
- El término independiente es
Ejemplo 2: Polinomio Cuadrático
Si consideramos el polinomio , podemos identificar en él los siguientes elementos:
- El grado es
- El coeficiente principal es
- El término independiente es
Nota: A un polinomio de grado igual a dos, se le conoce como Polinomio de Segundo Grado ó Polinomio Cuadrático.
Ejemplo 3: Polinomio Cúbico
Si consideramos el polinomio , podemos identificar en él los siguientes elementos:
- El grado es
- El coeficiente principal es
- El término independiente es
Nota: A un polinomio de grado igual a tres, se le conoce como Polinomio de Tercer Grado ó Polinomio Cúbico.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Al definir herramientas basadas en los polinomios, puede resultar necesario tomar en consideración algunas formas de reescribirlos, con el fin de estandarizar la forma en que estos se expresan.
Ejemplo 4: Completar un polinomio
Si consideramos el polinomio , podemos identificar en él los siguientes elementos:
- El grado es
- El coeficiente principal es
- El término independiente es
Además, podemos notar que faltan las potencias 4 y 2 de . Como el cero es el elemento nulo del producto y además es el elemento neutro de la suma, podemos decir que los coeficientes que multiplican a
y
son iguales a cero, por esta razón no hace falta escribir esos sumandos. Sin embargo podemos completar el polinomio de la siguiente manera:
Ejemplo 5: Reordenar un polinomio
Si consideramos el polinomio , podemos identificar en él los siguientes elementos:
- El grado es
- El coeficiente principal es
- El término independiente es
Además, podemos notar que la mayor potencia aparece como un primer sumando, pero, como la suma es conmutativa, nosotros podemos reordenar los sumandos del polinomio de modo que las potencias se escriban en orden decreciente de la siguiente manera:
Ejemplo 6: Agrupación de términos
Si consideramos el polinomio , podemos notar que los términos
,
aparecen dos veces, además, ¿hay dos términos independientes? En este caso podemos agrupar los términos semejantes, para esto recurrimos a la propiedad distributiva de la suma y multiplicación (particular mente a sacar el factor común de una suma), y además de la propiedad asociativa de la suma para reescribir el polinomio de la siguiente forma:
Una vez que hemos agrupado los términos semejantes, podemos identificar en él los siguientes elementos:
- El grado es
- El coeficiente principal es
- El término independiente es
Definir polinomios nos proveerá maleabilidad sobre distintas expresiones matemáticas, que de momento no comprenderemos. Entender como está definido un polinomio y saber identificar sus elementos nos permitirá desarrollar herramientas sofisticadas para análisis complejos.
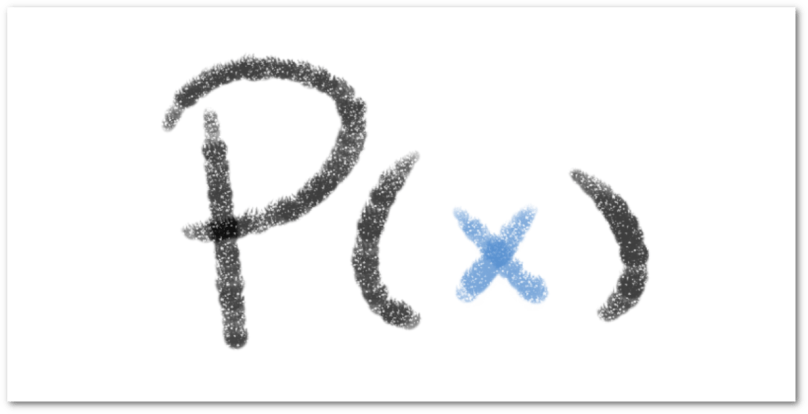


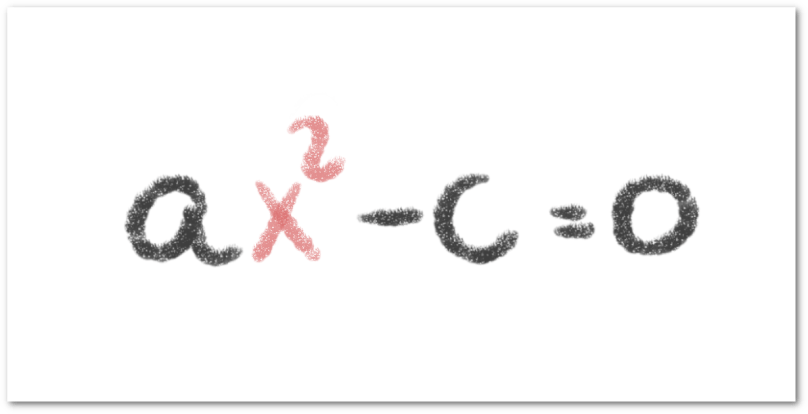


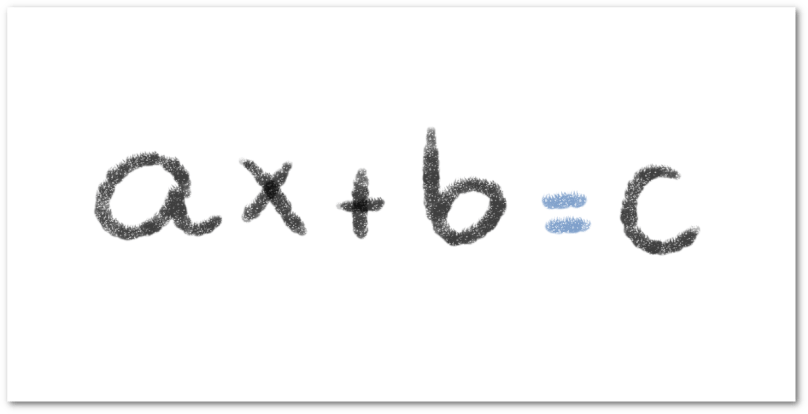
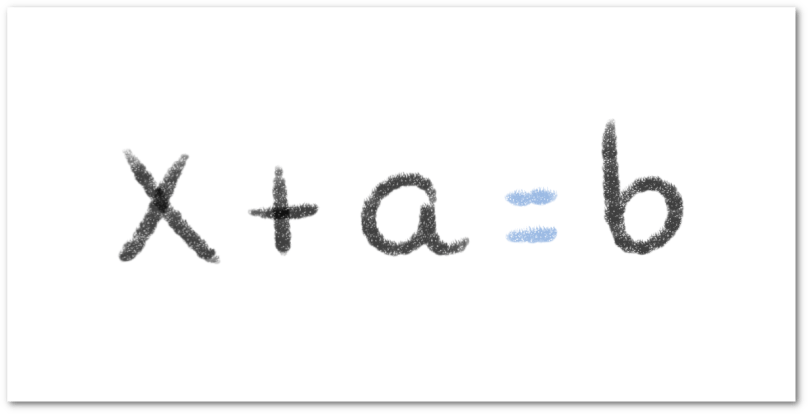
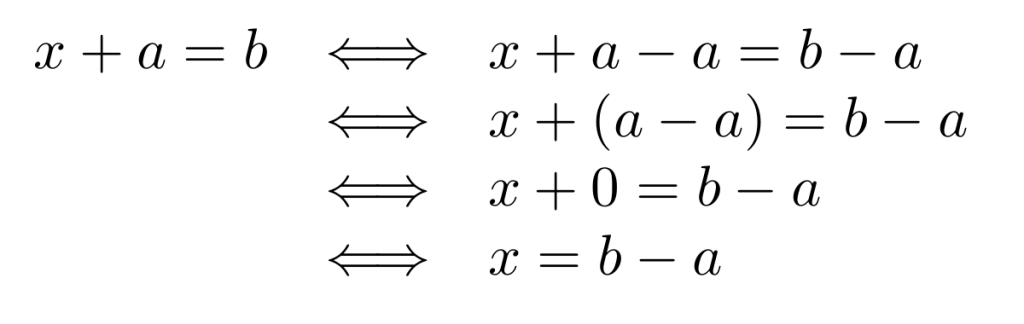
Debe estar conectado para enviar un comentario.