Acotando variables
Suponga que usted debe llenar una pequeña piscina inflable con agua, ésta tiene actualmente treinta litros de agua, pero no puede cargar menos de cuarenta litros porque se desinfla y no debe cargar más de ochenta porque se derrama, ¿cuánta agua puede verter en esta piscina? Éste tipo de situaciones la podemos expresar con una inecuación en la que acotamos un número desconocido por otros dos de la siguiente forma:
Al introducir las inecuaciones lineales, las hemos definido usando sólo una desigualdad y calculamos la solución de estas usando técnicas de despeje muy similares a las usadas al calcular la solución de ecuaciones, que también contaban con sólo una igualdad.
En este caso notamos que la inecuación que se presenta cuenta con dos desigualdades, así que surge la siguiente pregunta: ¿de qué forma podemos aplicar las técnicas de despeje cuando hay dos desigualdades en la inecuación?
También pudiera interesarte
Cómo calcular la solución
La técnica para calcular la solución de una inecuación lineal con dos desigualdades consiste en fraccionarlas en dos inecuaciones lineales y esta forma, poder aplicar las técnicas de despeje en cada una.
Formalmente, si consideramos ,
,
y
números reales, podemos expresar una inecuación lineal con dos desigualdades de la siguiente forma:
Los valores de que satisfacen las inecuación
son exactamente los mismos que satisfacen las siguientes dos inecuaciones al mismo tiempo:
Ejemplos
Ejemplo 1
Para calcular los valores de que satisfacen la inecuación que hemos planteado al inicio de esta sección, debemos calcular la solución de cada una de estas inecuaciones por separado. Entonces, considerando la inecuación original
, tenemos dos inecuaciones
Inecuación 1
Inecuación 2
A partir de estas dos inecuaciones, definimos dos conjuntos de soluciones expresados de forma comprensiva y de forma gráfica sobre la recta real:
Solución 1:

Solución 2:

Al considerar estas dos soluciones, debemos tomar en cuenta que los valores de que satisfacen la inecuación
son los que se encuentran en estos dos conjuntos al mismo tiempo, es decir, se encuentra en la intersección de estos dos conjuntos. Por lo tanto
se encuentra en el siguiente conjunto

Notemos que gráficamente, los elementos de nuestra solución se encuentran en el área donde se cruzan las líneas, es decir, entre 10 y 50. Así, concluimos que se pueden verter entre diez y cincuenta litros de agua a la piscina inflable para que ésta se pueda usar con tranquilidad.
Nota: Si consideramos a menor que b, es lo mismo que considerar b mayor que a. Es decir, y
son expresiones equivalentes.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 2
Calcule los valores de que satisfacen la siguiente desigualdad, escriba el conjunto solución de forma comprensiva y dibuje una representación gráfica de la solución en la recta real.
Inecuación 1
Inecuación 2
A partir de estas dos inecuaciones, definimos dos conjuntos de soluciones expresados de forma comprensiva y de forma gráfica sobre la recta real:
Solución 1:

Solución 2:

Al considerar estas dos soluciones, debemos tomar en cuenta que los valores de que satisfacen la inecuación
son los que se encuentran en estos dos conjuntos al mismo tiempo, es decir, se encuentra en la intersección de estos dos conjuntos. Por lo tanto
se encuentra en el siguiente conjunto
Gráficamente, los elementos de nuestra solución se encuentran en el área donde se cruzan las líneas, es decir, entre y
.

Ejemplo 3
Calcule los valores de que satisfacen la siguiente desigualdad, escriba el conjunto solución de forma comprensiva y haga una representación gráfica de la solución en la recta real.
Inecuación 1
Inecuación 2
A partir de estas dos inecuaciones, definimos dos conjuntos de soluciones expresados de forma comprensiva y de forma gráfica sobre la recta real:
Solución 1:

Solución 2:

Al considerar estas dos soluciones, debemos tomar en cuenta que los valores de que satisfacen la inecuación
son los que se encuentran en estos dos conjuntos al mismo tiempo, es decir, se encuentra en la intersección de estos dos conjuntos. Por lo tanto
se encuentra en el siguiente conjunto
Gráficamente, los elementos de nuestra solución se encuentran en el área donde se cruzan las líneas, es decir, entre y
.

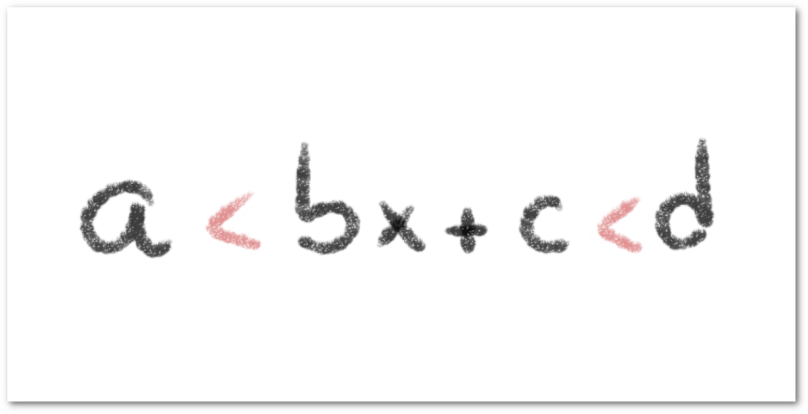








Debe estar conectado para enviar un comentario.