- Propiedades de la Integral Definida
- Área entre dos curvas
- Ejemplos
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
- Ejercicios Propuestos por los usuarios de totumat
- Ejercicio 1
Propiedades de la Integral Definida
Al calcular áreas usando el Teorema Fundamental del Cálculo, no siempre encontraremos funciones elementales positivas, es por esto que debemos contar con herramientas para abordar áreas definidas por otro tipo de funciones. A continuación se presentan una serie de propiedades de la integral definida que permiten ampliar el espectro de áreas bajo curvas que podemos calcular.
También pudiera interesarte
Sean  y
y  dos funciones continuas en un intervalo
dos funciones continuas en un intervalo ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) ,
, 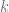 un escalar y
un escalar y  un elemento de
un elemento de ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) , entonces tenemos que
, entonces tenemos que
Las primeras tres propiedades son análogas a las propiedades vistas en la integral indefinida y hacen referencia a la suma, resta y multiplicación por un escalar de funciones.
La siguiente propiedad nos permite comparar el tamaño del área bajo la curva que definen dos funciones considerando la forma en que estas están relacionadas.
Esta propiedad indica que al intercambiar los límites de integración, cambia el signo de la integral.
Las siguientes propiedades indican que si la función es cero entonces su integral será igual a cero y también que la integral definida sobre un sólo punto es igual a cero, respectivamente
Esta propiedad es muy interesante pues lo que indica que es que al calcular la integral de una función es posible partir el intervalo, de esta forma calcular la integral una parte de la función por un lado y otra parte por otro lado, finalmente se pueden juntar los resultados.
Área entre dos curvas
El método que hemos usado para calcular áreas resulta motivado para calcular áreas bajo curvas definidas por funciones positivas, así que es inevitable preguntarse, ¿qué ocurre si la función es negativa? Supongamos que queremos calcular el área bajo la curva  en el intervalo
en el intervalo ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) .
.
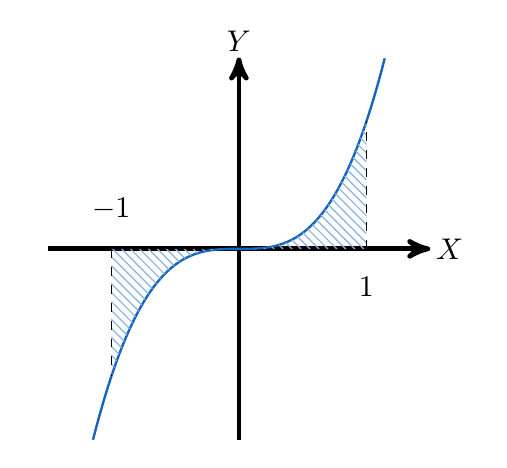
Identificamos el área que queremos calcular
Si aplicamos directamente el Teorema Fundamental del Cálculo, tenemos que
Sin embargo, esto es intuitivamente imposible pues al menos gráficamente podemos identificar el área bajo la curva y no pareciera ser igual a cero. Considerando esto en cuenta, debemos abordar este problema de una forma diferente.
Para entender lo que está pasando debemos recordar que al definir la Sumas de Riemann, calculamos el área de rectángulos cuyas alturas venían dadas por las imágenes de la función, así que al calcular el área cuando la función es negativa, el resultado de la integral será negativo.
Por ahora diremos que basta multiplicar por menos uno (-1) el resultado negativo de la integral para obtener el valor del área, aunque veremos luego veremos cómo solventar esta situación formalmente.
Entonces, para calcular el área bajo la curva  en el intervalo
en el intervalo ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) debemos partir el intervalo en dos partes, uno en el que las imágenes de la función son negativas y otro en el que las imágenes de la función son positivas, a simple vista podemos ver que esto pasa cuando
debemos partir el intervalo en dos partes, uno en el que las imágenes de la función son negativas y otro en el que las imágenes de la función son positivas, a simple vista podemos ver que esto pasa cuando  está en
está en ![[-1,0]](https://s0.wp.com/latex.php?latex=%5B-1%2C0%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) y cuando
y cuando  está en
está en ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) , respectivamente. Entonces podemos identificar dos áreas
, respectivamente. Entonces podemos identificar dos áreas  y
y 
Gracias a las propiedades del la Integral Definida podemos partir la integral que hemos planteado como 
Si aplicamos el Teorema Fundamental del Cálculo para cada una de estas integrales, tenemos que
Finalmente, el área que queremos calcular estará determinada por la suma de estas dos áreas, es decir,

Calcular el área por debajo de una curva que está debajo del Eje X pierde sentido literario, tampoco tiene mucho sentido hablar de áreas negativas. Es por esto que simplemente multiplicar por menos uno no parece una respuesta satisfactoria cuando calculamos áreas si la función tiene imágenes negativas. Es por esto que debemos generalizar nuestra motivación para replantear el enfoque de la integral definida y definirla no como el área bajo la curva si no como el área encerrada entre la curva y el Eje X.
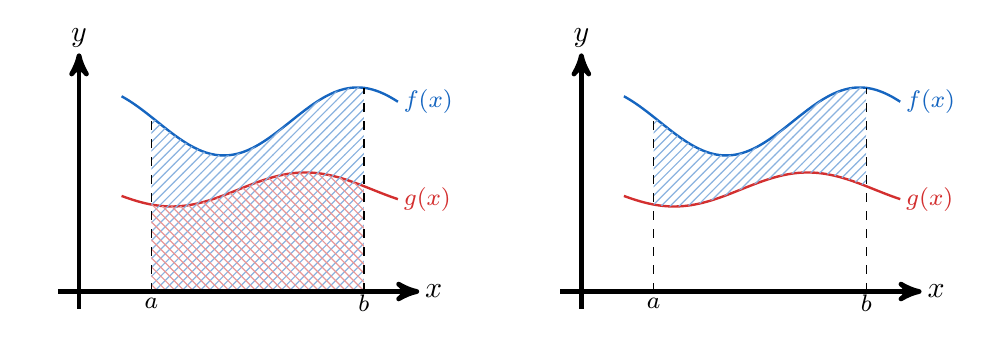
Es posible determinar el área entre dos curvas basándose en la forma que calculamos la longitud de un intervalo, es decir, tomando el valor más grande y restándole el valor más pequeño. De esta forma, si consideramos dos funciones  continuas en un intervalo
continuas en un intervalo ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) , podemos calcular el área encerrada entre las curvas que definen tomando el área de la función
, podemos calcular el área encerrada entre las curvas que definen tomando el área de la función  que está por encima y le restamos el área la función
que está por encima y le restamos el área la función  que está por debajo,
que está por debajo,
Por lo tanto, calculamos el área entre las curvas que definen las funciones  y
y  de la siguiente forma:
de la siguiente forma:
Vemos con algunos ejemplos como calcular encerradas entre curvas.
Ejemplos
Ejemplo 1
Calcule el área encerrada entre las curvas  y
y  en el intervalo
en el intervalo ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) .
.
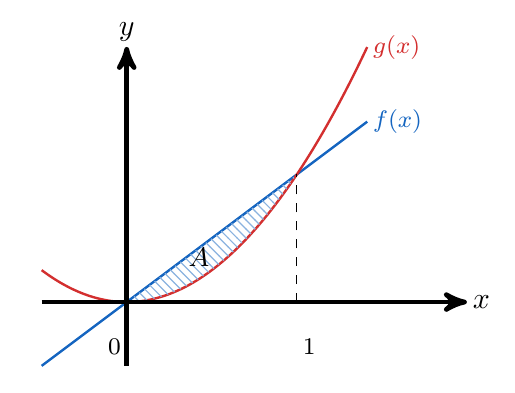
Identificamos el área que queremos calcular
Notamos que la función  está por encima del la función
está por encima del la función  . Entonces el área se calcula con la siguiente resta de integrales
. Entonces el área se calcula con la siguiente resta de integrales
Este ejemplo nos señala el porqué basta con multiplicar por menos uno al calcular el área bajo la curva de una de una función con imágenes negativas.
Ejemplo 2
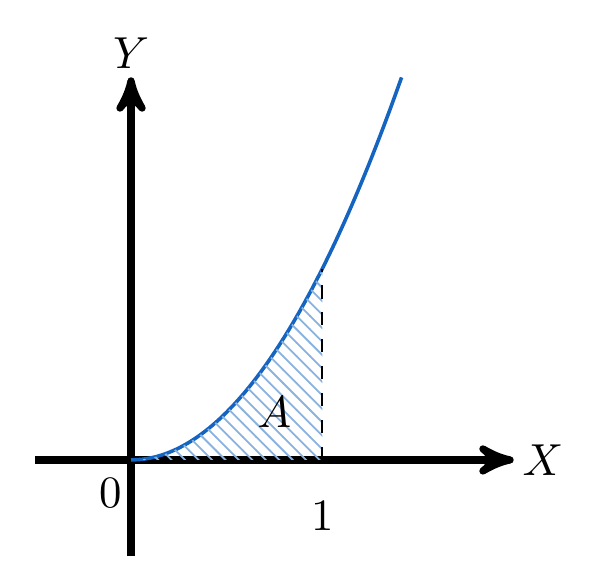
Calcule el área encerrada entre las curvas 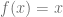 y
y 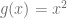 en el intervalo
en el intervalo ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) .
.
Identificamos el área que queremos calcular
Notamos que la función  está por encima del la función
está por encima del la función  . Entonces el área se calcula con la siguiente resta de integrales
. Entonces el área se calcula con la siguiente resta de integrales
Ejemplo 3
Calcule el área encerrada entre las curvas  y
y 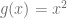 en el intervalo
en el intervalo ![[-1,3]](https://s0.wp.com/latex.php?latex=%5B-1%2C3%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) .
.
En los ejemplos anteriores los puntos de intersección entre ambas funciones eran obvios y así fue bastante claro determinar los puntos en los que unas función estaba por encima de la otra, sin embargo, esto no siempre es así.
Antes de identificar el área que se debe calcular, es necesario calcular los puntos de intersección entre ambas funciones y así apreciar los puntos en los que la una función pasa a estar encima de la otra.
Para calcular los puntos de intersección entre dos funciones, basta con igualar las expresiones que las definen, es decir,

En este caso podemos agrupar todos los elementos de un sólo lado de la ecuación para plantear una ecuación cuadrática de la siguiente forma

Y aplicando el método de su preferencia para calcular la solución de una ecuación cuadrática, obtenemos que los puntos de intersección entre las dos funciones son  y
y  , notando que ambos están dentro del intervalo dado. Identificamos el área que queremos calcular
, notando que ambos están dentro del intervalo dado. Identificamos el área que queremos calcular
Entonces, para calcular el área debemos partir el intervalo en tres partes, ya que funciones involucradas se relacionan de forma diferente en cada una de estas partes. Entonces tenemos que calcular tres áreas y posteriormente sumarlas.
Notamos que la función  está por encima de la función
está por encima de la función  en el intervalo
en el intervalo ![[-1,0]](https://s0.wp.com/latex.php?latex=%5B-1%2C0%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) . Entonces el área se calcula con la siguiente resta de integrales
. Entonces el área se calcula con la siguiente resta de integrales
Notamos que la función  está por encima de la función
está por encima de la función  en el intervalo
en el intervalo ![[0,2]](https://s0.wp.com/latex.php?latex=%5B0%2C2%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) . Entonces el área se calcula con la siguiente resta de integrales
. Entonces el área se calcula con la siguiente resta de integrales
Notamos que la función  está por encima de la función
está por encima de la función  en el intervalo
en el intervalo ![[2,1]](https://s0.wp.com/latex.php?latex=%5B2%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) . Entonces el área se calcula con la siguiente resta de integrales
. Entonces el área se calcula con la siguiente resta de integrales
Finalmente, el área que queremos calcular estará determinada por la suma de estas tres áreas, es decir,
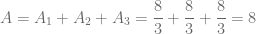
Ejercicios Propuestos por los usuarios de totumat
Ejercicio 1
Calcule el área encerrada entre las curvas  y
y  .
.
Lo primero que debemos notar es que estas funciones están expresadas de forma implícita, así que será necesario reescribirlas como  en función de
en función de  para estudiar su gráfica en el plano cartesiano. Entonces,
para estudiar su gráfica en el plano cartesiano. Entonces,
Esto quiere decir que la función  representa ambas funciones
representa ambas funciones  y
y  al mismo tiempo. Por otra parte, tenemos,
al mismo tiempo. Por otra parte, tenemos,
Esto quiere decir que la función 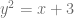 representa ambas funciones
representa ambas funciones  y
y  al mismo tiempo.
al mismo tiempo.
Para calcular los puntos de intersección entre estas dos funciones, debemos plantear un sistema de ecuaciones de dos ecuaciones y dos incógnitas, de la siguiente manera

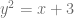
Para hallar la solución de este sistema de ecuaciones, restamos los elementos correspondientes de cada ecuación para obtener la siguiente ecuación:
De esta forma, concluimos que estas dos funciones se cortan cuando 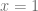 , es decir, en los puntos
, es decir, en los puntos  y
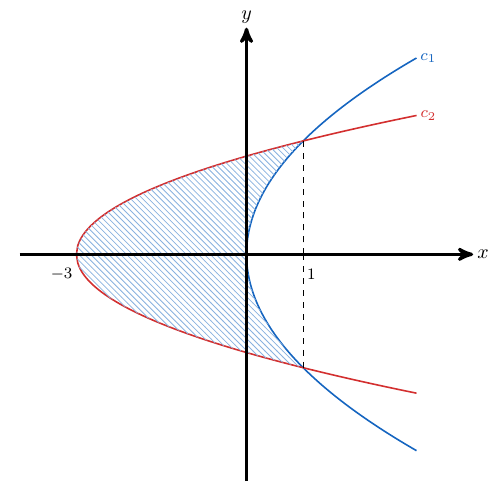
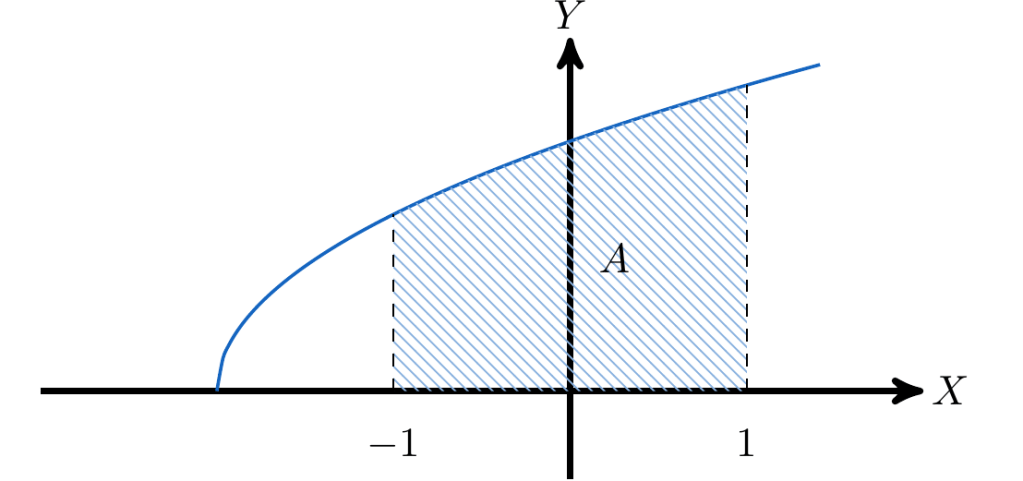
y  . Identificamos el área que queremos calcular,
. Identificamos el área que queremos calcular,
Ya que hemos identificado el área que queremos calcular, podemos notar que esta es simétrica respecto al Eje X. Este hecho presenta una ventaja para hacer este cálculo, pues bastará con calcular sólo la mitad del área, ya sea la mitad superior o la mitad inferior, y posteriormente multiplicarla por dos. En este caso, procederemos a calcular la mitad superior:
Entonces, para calcular el área debemos partir el intervalo en dos partes, ya que curvas involucradas se relacionan de forma diferente en cada una de estas partes. Entonces tenemos que calcular dos áreas y posteriormente sumarlas.
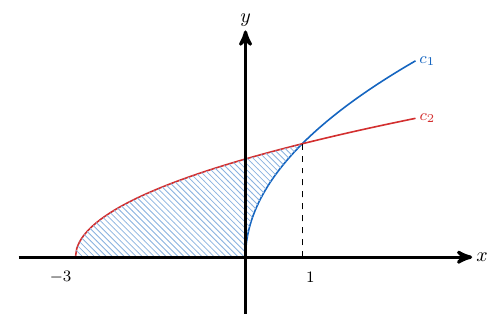
Notamos que la curva 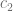 está por encima del Eje X en el intervalo
está por encima del Eje X en el intervalo ![[-3,0]](https://s0.wp.com/latex.php?latex=%5B-3%2C0%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) . Entonces el área se calcula con la siguiente integral
. Entonces el área se calcula con la siguiente integral
Notamos que la curva 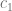 está por encima de la curva
está por encima de la curva 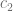 en el intervalo
en el intervalo ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=5e5e5e&s=0&c=20201002) . Entonces el área se calcula con la siguiente integral
. Entonces el área se calcula con la siguiente integral
Finalmente, el área que queremos calcular estará determinada por la suma de estas dos áreas multiplicadas por dos, es decir,

y
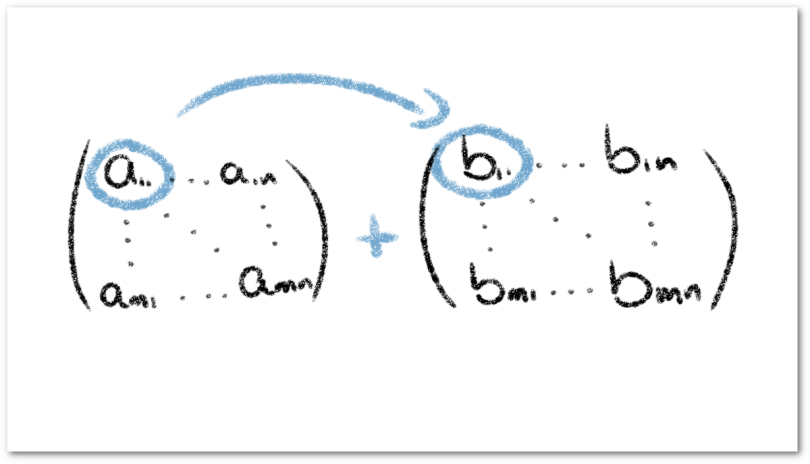
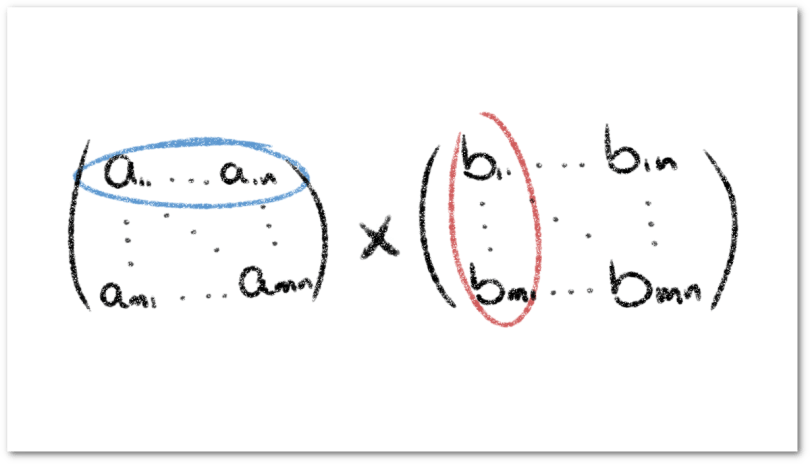
dos matrices de tamaño
, definimos la suma
como una nueva matriz donde cada elemento
de esta nueva matriz, está definido como la suma del elemento
de la matriz
más el elemento
de la matriz
. Formalmente,

, calcule la suma indicada.


, calcule la suma indicada.


calcule la suma indicada.


calcule la suma indicada.



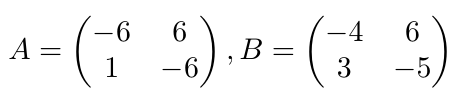



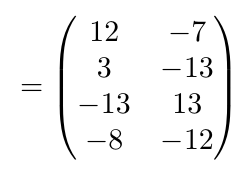









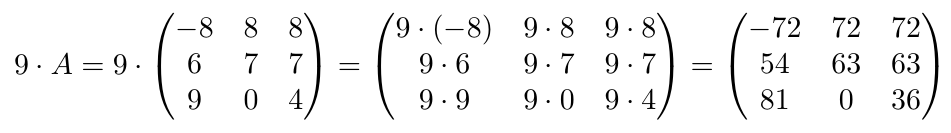




































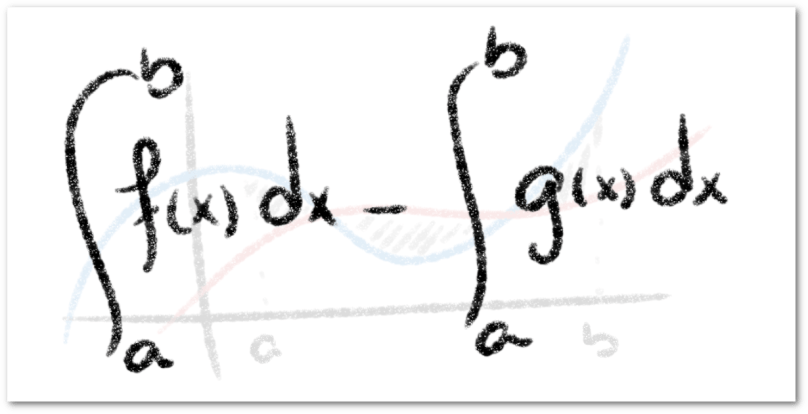
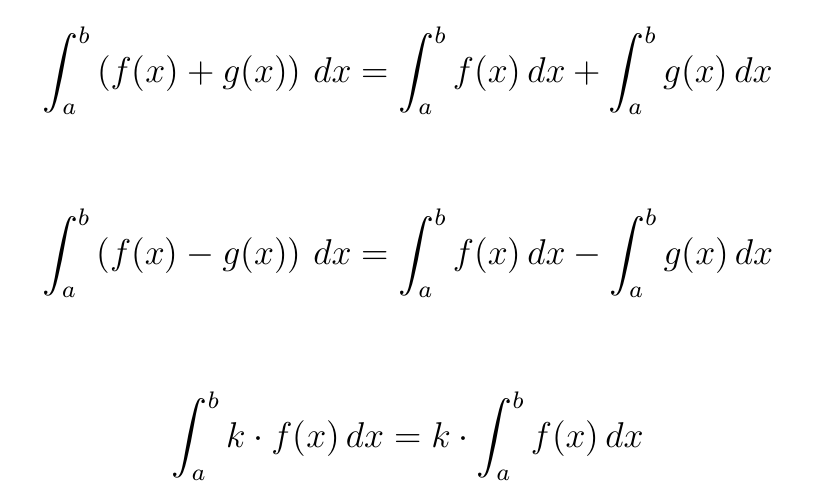
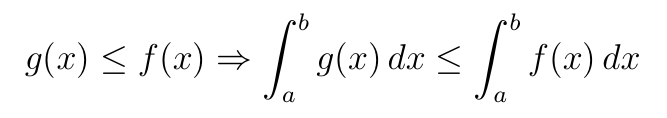
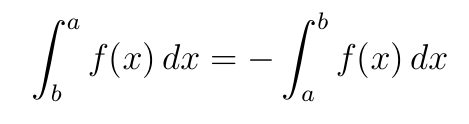

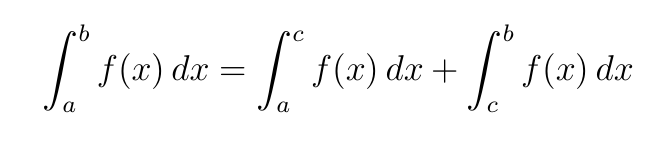

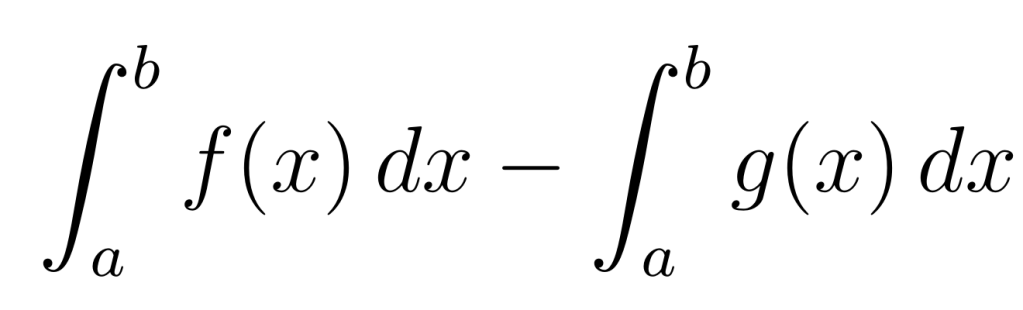
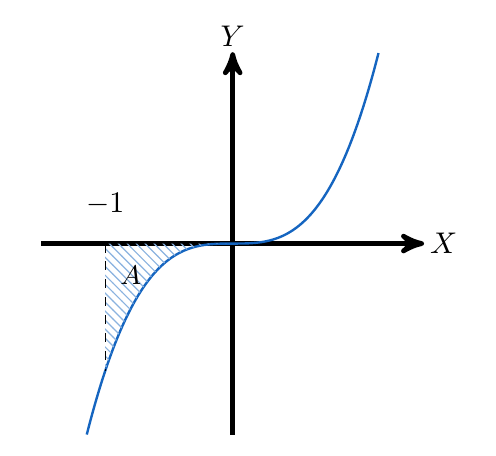
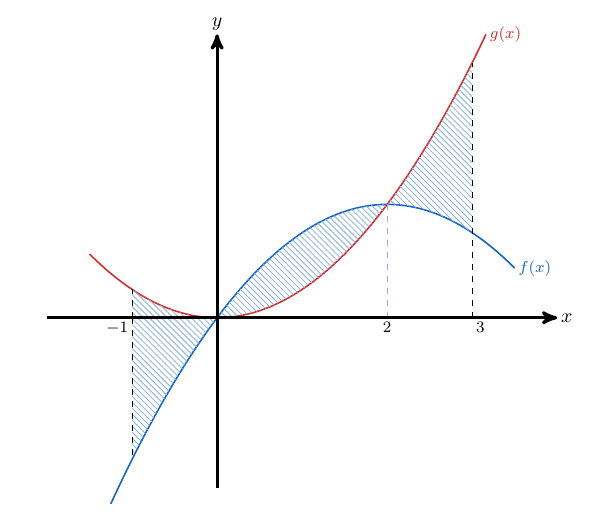
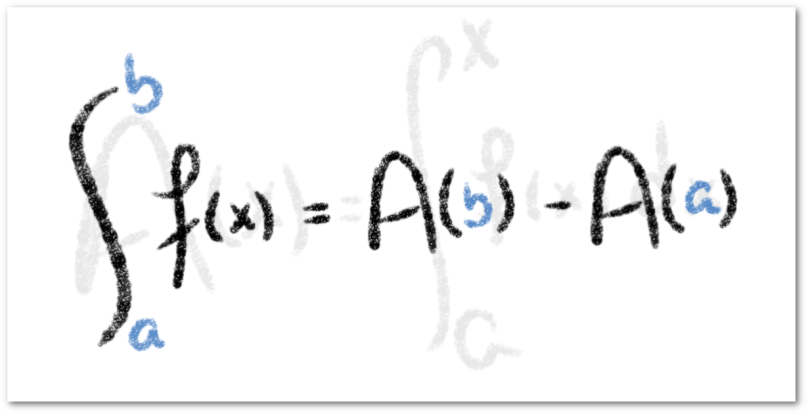

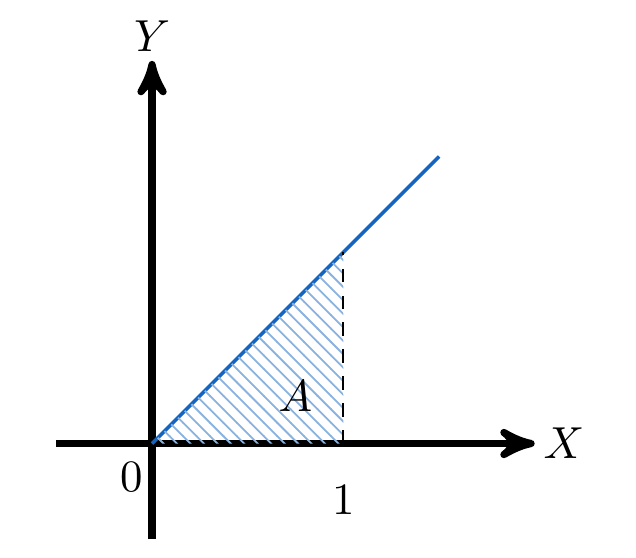
Debe estar conectado para enviar un comentario.