Etiqueta: Polinomios

Ejercicios Propuestos

Ejercicios Propuestos – Operaciones entre polinomios

Anthonny Arias García1 comentario
Anuncios

Suma de Polinomios

Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.

Considerando los polinomios P(x) y Q(x), calcule P(x) + Q(x).

  1. P(x) = x^{2} + 12 x + 35
    Q(x) = x - 6
  2. P(x) = x^{2} + 13 x + 40
    Q(x) = x + 6
  3. P(x) = x^{2} - 14 x + 48
    Q(x) = x + 7
  4. P(x) = x^{2} - 2 x - 15
    Q(x) = x
  1. P(x) = 2 x^{2} + 14 x + 12
    Q(x) = - 6 x^{2} + 54 x - 120
  2. P(x) = - 2 x^{2} - 14 x
    Q(x) = 8 x^{2} - 128 x + 504
  3. P(x) = 3 x^{2} + 42 x + 120
    Q(x) = x^{2} + x - 72
  4. P(x) = 4 x^{2} - 24 x - 64
    Q(x) = 3 x^{2} + 57 x + 270
  1. P(x) = - x^{3} - 3 x^{2} + 40 x + 84
    Q(x) = 8 x^{3} - 144 x^{2} + 648 x
  2. P(x) = - 6 x^{3} + 126 x^{2} - 840 x + 1728
    Q(x) = - 7 x^{3} - 7 x^{2} + 182 x - 168
  3. P(x) = - 10 x^{3} - 30 x^{2} + 760 x + 2880
    Q(x) = 8 x^{3} - 168 x^{2} + 1120 x - 2304
  4. P(x) = - 9 x^{3} - 198 x^{2} - 1413 x - 3240
    Q(x) = 9 x^{3} + 63 x^{2} - 900 x - 6300
  1. P(x) = 8 x^{4} - 600 x^{2} - 2000 x
    Q(x) = 6 x^{4} - 48 x^{3} - 246 x^{2} + 1368 x + 3240
  2. P(x) = - 10 x^{4} - 160 x^{3} - 690 x^{2} + 100 x + 4000
    Q(x) = x^{4} + 2 x^{3} - 59 x^{2} + 48 x + 108
  3. P(x) = - 3 x^{4} - 51 x^{3} - 186 x^{2} + 744 x + 4032
    Q(x) = 7 x^{4} + 70 x^{3} + 49 x^{2} - 126 x
  4. P(x) = - 2 x^{4} - 22 x^{3} + 32 x^{2} + 472 x - 480
    Q(x) = - 4 x^{4} - 48 x^{3} + 132 x^{2} + 1760 x - 3600
Anuncios

Resta de Polinomios

Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.

Considerando los polinomios P(x) y Q(x), calcule P(x) - Q(x).

  1. P(x) = x^{2} - x - 90
    Q(x) = x + 9
  2. P(x) = x^{2} + 8 x + 15
    Q(x) = x - 8
  3. P(x) = x^{2} - 11 x + 18
    Q(x) = x - 3
  4. P(x) = x^{2} + 6 x + 5
    Q(x) = x + 6
  1. P(x) = 5 x^{2} - 45 x + 70
    Q(x) = 7 x^{2} + 49 x + 84
  2. P(x) = 9 x^{2} + 108 x + 180
    Q(x) = 6 x^{2} - 24 x - 270
  3. P(x) = 6 x^{2} - 90 x + 300
    Q(x) = 2 x^{2} + 22 x + 56
  4. P(x) = 9 x^{2} + 144 x + 567
    Q(x) = - 4 x^{2} + 20 x + 144
  1. P(x) = - 10 x^{3} + 170 x^{2} - 880 x + 1440
    Q(x) = 9 x^{3} - 45 x^{2} - 252 x + 288
  2. P(x) = - 4 x^{3} - 32 x^{2} + 100 x + 800
    Q(x) = - 2 x^{3} + 2 x^{2} + 92 x + 160
  3. P(x) = 6 x^{3} + 12 x^{2} - 258 x + 240
    Q(x) = 5 x^{3} - 60 x^{2} + 160 x
  4. P(x) = 10 x^{3} + 180 x^{2} + 1070 x + 2100
    Q(x) = - 5 x^{3} + 40 x^{2} + 100 x
  1. P(x) = 9 x^{4} - 216 x^{3} + 1800 x^{2} - 6048 x + 6480
    Q(x) = - x^{4} - 14 x^{3} - 53 x^{2} - 40 x
  2. P(x) = - 6 x^{4} - 60 x^{3} + 360 x^{2} + 4860 x + 10206
    Q(x) = - 3 x^{4} - 33 x^{3} + 165 x^{2} + 2625 x + 6750
  3. P(x) = x^{4} - 12 x^{3} + 27 x^{2}
    Q(x) = 8 x^{4} - 64 x^{3} - 552 x^{2} + 5184 x - 7776
  4. P(x) = 10 x^{4} - 60 x^{3} - 320 x^{2} + 1500 x + 1750
    Q(x) = 10 x^{4} - 230 x^{3} + 1740 x^{2} - 4720 x + 3200
Anuncios

Producto de Polinomios

Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.

Considerando los polinomios P(x) y Q(x), calcule P(x) \cdot Q(x).

  1. P(x) = x^{2} + 19 x + 90
    Q(x) = x + 2
  2. P(x) = x^{2} + 20 x + 100
    Q(x) = x - 10
  3. P(x) = x^{2} + 11 x + 30
    Q(x) = x - 3
  4. P(x) = x^{2} + 7 x - 30
    Q(x) = x - 2
  1. P(x) = 6 x^{2} - 36 x + 54
    Q(x) = - 7 x^{2} - 28 x + 35
  2. P(x) = 9 x^{2} - 45 x
    Q(x) = - 3 x^{2} - 33 x - 30
  3. P(x) = - 6 x^{2} - 36 x + 42
    Q(x) = 108 - 3 x^{2}
  4. P(x) = 7 x^{2} + 28 x - 224
    Q(x) = - x^{2} - 2 x + 48
  1. P(x) = - x^{3} + 14 x^{2} - 55 x + 42
    Q(x) = - 6 x^{3} + 18 x^{2} + 198 x - 210
  2. P(x) = 7 x^{3} - 84 x^{2} - 28 x + 1680
    Q(x) = 2 x^{3} + 6 x^{2} - 98 x - 294
  3. P(x) = 4 x^{3} + 8 x^{2} - 284 x - 288
    Q(x) = 9 x^{3} + 27 x^{2} - 360 x - 756
  4. P(x) = - 10 x^{3} + 40 x^{2} + 10 x - 40
    Q(x) = 3 x^{3} - 36 x^{2} - 39 x + 1080
  1. P(x) = 6 x^{4} - 12 x^{3} - 450 x^{2} - 384 x + 840
    Q(x) = - 10 x^{4} - 180 x^{3} - 640 x^{2} + 2880 x + 12800
  2. P(x) = - 10 x^{4} + 370 x^{2} - 840 x
    Q(x) = - 8 x^{4} - 232 x^{3} - 2464 x^{2} - 11360 x - 19200
  3. P(x) = - 2 x^{4} - 2 x^{3} + 152 x^{2} - 328 x - 480
    Q(x) = - 10 x^{4} - 50 x^{3} + 710 x^{2} + 1650 x - 13500
  4. P(x) = 5 x^{4} - 75 x^{3} + 310 x^{2} + 60 x - 1800
    Q(x) = 4 x^{4} + 100 x^{3} + 900 x^{2} + 3420 x + 4536
Anuncios

Producto de Polinomios

Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.

Considerando los polinomios P(x) y Q(x), calcule P(x) \div Q(x).

  1. P(x) = x^{2} - x - 72
    Q(x) = x + 8
  2. P(x) = x^{2} - 64
    Q(x) = x + 3
  3. P(x) = x^{2} - 9
    Q(x) = x + 4
  4. P(x) = x^{2} - 2 x - 80
    Q(x) = x - 9
  1. P(x) = 10 x^{2} + 70 x
    Q(x) = 5 x + 30
  2. P(x) = - 24 x^{2} + 264 x - 576
    Q(x) = 6 x - 18
  3. P(x) = - 49 x^{2} + 637 x - 1470
    Q(x) = 7 x - 7
  4. P(x) = - 56 x^{2} - 280 x - 224
    Q(x) = 8 x + 8
  1. P(x) = 6 x^{3} - 6 x^{2} - 24 x + 24
    Q(x) = x - 10
  2. P(x) = - 7 x^{3} - 7 x^{2} + 455 x - 441
    Q(x) = x + 8
  3. P(x) = - 5 x^{3} - 20 x^{2} + 5 x + 20
    Q(x) = x + 3
  4. P(x) = 3 x^{3} + 9 x^{2} - 228 x - 864
    Q(x) = x + 7
  1. P(x) = - 9 x^{4} - 54 x^{3} + 225 x^{2} - 162 x
    Q(x) = x + 1
  2. P(x) = - 5 x^{4} + 50 x^{3} + 35 x^{2} - 320 x - 300
    Q(x) = x + 8
  3. P(x) = - 5 x^{4} + 35 x^{3} + 590 x^{2} - 3500 x - 9000
    Q(x) = x
  4. P(x) = 9 x^{4} + 72 x^{3} - 945 x^{2} - 4500 x + 31500
    Q(x) = x + 3
Anuncios
Anuncio publicitario

Expresiones Racionales

Anthonny Arias GarcíaDeja un comentario

Habiendo estudiado las operaciones entre polinomios, particularmente la división de polinomios, podemos ampliar las operaciones entre fracciones como una herramienta para simplificar las operaciones entre polinomios antes de efectuarlas.

También pudiera interesarte

Anuncios

Definimos una expresión racional como el cociente entre dos polinomios. Formalmente, si P(x) y Q(x) son dos polinomios con Q(x) \neq 0, entonces el siguiente cociente será una expresión racional:

\dfrac{P(x)}{Q(x)}

Diremos que P(x) es el numerador (o dividendo) de la expresión y Q(x) es el denominador (o divisor) de la expresión. En este caso, al ser, P(x) y Q(x) polinomios, este tipo de expresiones racionales serán expresiones algebraicas racionales.

Operaciones entre Expresiones Racionales

Las operaciones entre expresiones racionales se efectúan de la misma forma en que se efectúan las operaciones entre fracciones, es decir, si A(x), B(x), C(x) y D(x) son polinomios, con B(x) y D(x) distintos de cero, definimos:

Suma de Expresiones Racionales

\dfrac{A(x)}{B(x)} + \dfrac{C(x)}{D(x)} = \dfrac{A(x) \cdot D(x) + B(x) \cdot C(x)}{B(x) \cdot D(x)}

Resta de Expresiones Racionales

\dfrac{A(x)}{B(x)} - \dfrac{C(x)}{D(x)} = \dfrac{A(x) \cdot D(x) - B(x) \cdot C(x)}{B(x) \cdot D(x)}

Multiplicación de Expresiones Racionales

\dfrac{A(x)}{B(x)} \cdot \dfrac{C(x)}{D(x)} = \dfrac{A(x) \cdot C(x)}{B(x) \cdot D(x)}

División de Expresiones Racionales

\dfrac{A(x)}{B(x)} \div \dfrac{C(x)}{D(x)} = \dfrac{A(x) \cdot D(x)}{B(x) \cdot C(x)}

Anuncios

El objetivo de plantear expresiones racionales es el de simplificar expresiones que a primera vista parezcan complicadas o engorrosas para trabajar. Veamos en los siguientes ejemplos como efectuar operaciones entre expresiones racionales y de ser posible, su simplificación.

Ejemplos

Ejemplo 1

Efectúe la suma de las expresiones racionales \frac{2x+5}{2x+3} y \frac{6x+4}{8x+3}, y de ser posible, simplifique el resultado.

\dfrac{2x+5}{2x+3} + \dfrac{6x+4}{8x+3}

= \dfrac{(2x+5) \cdot (8x+3) + (2x+3) \cdot (6x+4)}{(2x+3) \cdot (8x+3)}

= \dfrac{ 16x^2 + 6x + 40x + 15 + 12x^2 + 8x + 18x + 12 }{(2x+3) \cdot (8x+3)}

= \dfrac{ 28x^2 + 72x + 27 }{(2x+3) \cdot (8x+3)}

Notemos que en el numerador se efectuó la propiedad distributiva en ambos sumandos para poder sumar los elementos comunes, sin embargo, en el denominador no hizo falta aplicar la propiedad distributiva, pues ya la expresión estaba factorizada.

Ejemplo 2

Efectúe la resta de las expresiones racionales \frac{7x-2}{3x+1} menos \frac{5x+2}{2x+4}, y de ser posible, simplifique el resultado.

\dfrac{7x-2}{3x+1} - \dfrac{5x+2}{2x+4}

= \dfrac{(7x-2) \cdot (2x+4) + (3x+1) \cdot (5x+2)}{(3x+1) \cdot (2x+4)}

= \dfrac{ 14x^2 + 28x - 4x - 8 - (15x^2 + 6x + 5x + 2) }{(3x+1) \cdot 2 (x+2)}

= \dfrac{ -x^2 + 13x - 10 }{2(3x+1) \cdot (x+2)}

Anuncios

Ejemplo 3

Efectúe el producto de las expresiones racionales \frac{4x^2+6}{-7x+2} y \frac{4x-3}{2x^2+3}, y de ser posible, simplifique el resultado.

\dfrac{4x^2+6}{-7x+2} \cdot \dfrac{4x-3}{2x^2+3}

= \dfrac{(4x^2+6) \cdot (4x-3)}{(-7x+2) \cdot (2x^2+3)}

= \dfrac{2 (2x^2+3) \cdot (4x-3)}{(-7x+2) \cdot (2x^2+3)}

= 2 \cdot \dfrac{(2x^2+3) \cdot (4x-3)}{(-7x+2) \cdot (2x^2+3)}

= 2 \cdot \dfrac{ (4x-3) \cdot (2x^2+3)}{(-7x+2) \cdot (2x^2+3)}

= 2 \cdot \dfrac{(4x-3)}{(-7x+2)}

Operaciones entre polinomios

Anthonny Arias García2 comentarios

Podemos definir las operaciones de suma, resta, multiplicación y división entre polinomios como una generalización de las operaciones que hemos definido entre los números reales.

También pudiera interesarte

Anuncios

Suma de polinomios

Para sumar o restar polinomios, recurrimos a la propiedad asociativa de los números reales, pues agrupamos los sumandos que tengan la misma potencia de x como factor, de forma que si consideramos dos polinomios P(x) = a_m x^m + \ldots + a_1 x + a_0 y Q(x) = b_n x^n + \ldots + b_1 x + b_0, donde el grado de P(x) es mayor que el grado de Q(x), es decir, m \geq n; definimos la suma P(x)+Q(x) de la siguiente forma:

Suma de Polinomios | totumat.com

De igual forma, definimos la resta P(x)-Q(x) de la siguiente forma:

Suma de Polinomios | totumat.com

Notando que si el grado de P(x) es estrictamente mayor que el grado de Q(x), entonces completamos el polinomio Q(x) con coeficientes ceros, es decir, b_i = 0 para todo i > n.

Veamos con algunos ejemplos como efectuar la suma de polinomios.

Anuncios

Ejemplos

Ejemplo 1

Considerando los polinomios P(x) = 3x^2 - 5x + 2 y Q(x) = 7x + 1, calcule la suma P(x) + Q(x).

Suma de Polinomios | totumat.com

Por lo tanto, P(x) + Q(x) = 3 x^2 + 2x + 3.

Ejemplo 2

Considerando los polinomios P(x) = 4x^6 + x^4 - 2x^2 + 9x + 12 y Q(x) = 3x^6 - 8x^5 + 4x^4 + x - 3, calcule la suma P(x) + Q(x).

Suma de Polinomios | totumat.com

Por lo tanto, P(x) + Q(x) = 7x^6 + 8x^5 - 5x^4 - 2x^2 + 10x + 15.

Ejemplo 3

Considerando los polinomios P(x) = 6x^3 + 7x^2 - 4 y Q(x) = 2x + 3, calcule la resta P(x) - Q(x).

Suma de Polinomios | totumat.com

Por lo tanto, P(x) - Q(x) = 6x^3 + 7x^2 - 2x - 7.

Ejemplo 4

Considerando los polinomios P(x) = -12x^6 + 3x^5 + 3x^4 - x^2 + 8x + 5 y Q(x) = x^6 + 5x^5 + 2x^4 - 4x^3 - 10x^2 - x, calcule la resta P(x) - Q(x).

Suma de Polinomios | totumat.com

Por lo tanto, P(x) - Q(x) = 11x^6 - 2x^5 + x^4 + 4x^3 + 9x^2 + 9x + 5.

Anuncios

Producto de polinomios

Para multiplicar polinomios, recurrimos a la propiedad distributiva de los números reales, de forma que si consideramos dos polinomios P(x) = a_m x^m + \ldots + a_1 x + a_0 y Q(x) = b_n x^n + \ldots + b_1 x + b_0, podemos definir el producto de estos dos polinomios distribuyendo los productos de la siguiente forma

Producto o Multiplicación de Polinomios | totumat.com

Una vez que se ha expandido este producto, lo podemos expresar como una sumatoria de la siguiente manera:

\sum_{i=1}^n \sum_{j=1}^m a_i b_j x^{i+j}

Este procedimiento pudiera resultar extenso y la notación del caso general pareciera engorrosa, sin embargo, efectuar el producto de polinomios no es más que la aplicación de la propiedad distributiva para los números reales y la posterior aplicación de las propiedades de las potencias para sumar los exponentes.

Veamos en los siguientes ejemplos como calcular algunos productos entre polinomios.

Anuncios

Ejemplos

Ejemplo 5

Considerando los polinomios P(x) = 4 x + 3 y Q(x) = - 10 x - 4. Calcule el producto P(x) \cdot Q(X), es decir,

\left( 4 x + 3 \right) \cdot \left( - 10 x - 4 \right)

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

Producto o Multiplicación de Polinomios | totumat.com

Por lo tanto el producto de los polinomios P(x) y Q(x) es igual a

- 40 x^{2} - 46 x - 12

Ejemplo 6

Considerando los polinomios P(x) = 6 x^{2} - 8 x + 2 y Q(x) = x^{2} + 5 x + 6. Calcule el producto P(x) \cdot Q(X), es decir,

\left( 6 x^{2} - 8 x + 2 \right) \cdot \left( x^{2} + 5 x + 6 \right)

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

Producto o Multiplicación de Polinomios | totumat.com

Por lo tanto el producto de los polinomios P(x) y Q(x) es igual a

6 x^{4} + 22 x^{3} - 2 x^{2} - 38 x + 12

Ejemplo 7

Considerando los polinomios P(x) = 3 x^{2} - 6 x + 6 y Q(x) = - 9 x^{3} - 5 x^{2} + 4 x + 7. Calcule el producto P(x) \cdot Q(X), es decir,

\left( 3 x^{2} - 6 x + 6 \right) \cdot \left( - 9 x^{3} - 5 x^{2} + 4 x + 7 \right)

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

Producto o Multiplicación de Polinomios | totumat.com

Por lo tanto el producto de los polinomios P(x) y Q(x) es igual a

- 27 x^{5} + 39 x^{4} - 12 x^{3} - 33 x^{2} - 18 x + 42

Ejemplo 9

Considerando los polinomios P(x) = - 4 x^{3} + x^{2} - 2 x + 2 y Q(x) = 9 x^{2} - x + 4. Calcule el producto P(x) \cdot Q(X), es decir,

\left( - 4 x^{3} + x^{2} - 2 x + 2 \right) \cdot \left( 9 x^{2} - x + 4 \right)

Aplicamos la propiedad distributiva y escribimos los productos resultantes en orden para facilitar la suma de los sumandos correspondientes

Producto o Multiplicación de Polinomios | totumat.com

Por lo tanto el producto de los polinomios P(x) y Q(x) es igual a

- 36 x^{5} + 13 x^{4} - 35 x^{3} + 24 x^{2} - 10 x + 8

Anuncios

División de polinomios

Para definir la división entre polinomios, debemos hacer algunas observaciones sobre división entre números reales pues considerando p y q dos números enteros, al dividir p entre q, buscamos un número tal que al multiplicarlo por q el resultado sea exactamente p, es decir, un número entero c tal que

p = c \cdot q

En este caso, decimos que la división es exacta. Sin embargo, si no podemos encontrar este número, buscamos un número tal que al multiplicarlo por q, el resultado sea mayor de los enteros menores que p, es decir, un número entero c tal que

p = c \cdot q + r

Donde 0 < r < a. Esta propiedad se conoce como el algoritmo de la división. Al número r lo llamaremos el resto de la división y se puede calcular como r = p - c \cdot q. Además notemos que si la división es exacta, entonces el resto de la división es igual a cero, es decir, r=0. Veamos en los siguientes ejemplos como expresar algunas divisiones usando el algoritmo de la división.

Anuncios

Ejemplos

Ejemplo 9

Si dividimos 8 entre 4, entonces buscamos un número entero tal que al multiplicarlo por 4 el resultado sea o que está cerca de 8, particularmente el número que estamos buscando es 2 pues 2 \cdot 4 = 8 y de acuerdo con el algoritmo de la división, el resto es igual a 8 - 8 = 0, esto lo expresamos de la siguiente forma:

División de Números Enteros | totumat.com

Por lo tanto decimos que 8 = 2 \cdot 4 + 0. En este caso el resto es igual a cero, por lo tanto, decimos que la división es exacta.

Ejemplo 10

Si dividimos 13 entre 5, entonces buscamos un número entero tal que al multiplicarlo por 5 el resultado sea o que está cerca de 13, particularmente el número que estamos buscando es 2 pues 2 \cdot 5 = 10 y de acuerdo con el algoritmo de la división, el resto es igual a 13 - 10 = 3, esto lo expresamos de la siguiente forma:

División de Números Enteros | totumat.com

Por lo tanto decimos que 13 = 2 \cdot 5 + 3. En este caso el resto es distinto de cero, por lo tanto, decimos que la división no es exacta.

Ejemplo 11

Si dividimos 21 entre 4, entonces buscamos un número entero tal que al multiplicarlo por 4 el resultado sea o que está cerca de 21, particularmente el número que estamos buscando es 5 pues 5 \cdot 4 = 20 y de acuerdo con el algoritmo de la división, el resto es igual a 21 - 20 = 1, esto lo expresamos de la siguiente forma:

División de Números Enteros | totumat.com

Por lo tanto decimos que 21 = 5 \cdot 4 + 1. En este caso el resto es distinto de cero, por lo tanto, decimos que la división no es exacta.

Ejemplo 12

Si dividimos 21 entre 7, entonces buscamos un número entero tal que al multiplicarlo por 7 el resultado sea o que está cerca de 21, particularmente el número que estamos buscando es 3 pues 3 \cdot 7 = 21 y de acuerdo con el algoritmo de la división, el resto es igual a 21 - 21 = 1, esto lo expresamos de la siguiente forma:

División de Números Enteros | totumat.com

Por lo tanto decimos que 21 = 3 \cdot 7 + 0. En este caso el resto es igual a cero, por lo tanto, decimos que la división es exacta.

Anuncios

El algoritmo de la división se puede generalizar al operar entre polinomios. De modo que si consideramos P(x) y Q(x) dos polinomios tales que el grado de Q(x) es menor o igual que el grado de P(x), al dividir P(x) entre Q(x), buscamos un polinomio tal que al multiplicarlo por Q(x) el resultado sea exactamente P(x), es decir, un polinomio C(x) tal que

P(x) = C(x) \cdot Q(x)

En este caso, decimos que la división es exacta. Sin embargo, si no podemos encontrar este polinomio, buscamos un polinomio tal que al multiplicarlo por Q(x) el polinomio resultante tenga el mismo grado que P(x) y que el grado del polinomio que define el resto sea menor que el grado de Q(x), es decir, un polinomio C(x) tal que

P(x) = C(x) \cdot Q(x) + R(x)

Donde gr\left( R(x) \right) < gr\left( Q(x) \right) \leq gr\left( P(x) \right). Además notemos que si la división es exacta, entonces el resto de la división es igual a cero, es decir, R(x) = 0. Veamos en los siguientes ejemplos el método para dividir polinomios y además, como expresar estas divisiones usando el algoritmo de la división.

Anuncios

Ejemplos

Ejemplo 13

Si dividimos el polinomio P(x) = x^2 + x + 3 entre el polinomio Q(x) = x + 1, entonces los escribimos de la siguiente forma

División de Polinomios | totumat.com

El siguiente paso será buscar un polinomio tal que al multiplicarlo por el primer sumando del polinomio Q(x) = x + 1 el resultado sea exactamente igual al primer sumando del polinomio P(x) = x^2 + x + 3, en este caso el polinomio que estamos buscando es x y lo escribimos de la siguiente forma

División de Polinomios | totumat.com

El siguiente paso será multiplicar el polinomio Q(x) = x + 1 por x y el resultado se lo restamos al polinomio P(x) = x^2 + x + 3 de la siguiente forma

División de Polinomios | totumat.com

Notamos que el grado del polinomio en el resto es menor que el grado del polinomio Q(x), Por lo tanto, concluimos que

x^2 + x + 3 = x \cdot (x+1) + 3

Ejemplo 14

Si dividimos el polinomio P(x) = 8x^3 - 6x^2 - 2 entre el polinomio Q(x) = 2x^2 + x - 1, entonces completamos los polinomios incompletos y los escribimos de la siguiente forma

División de Polinomios | totumat.com

El siguiente paso será buscar un polinomio tal que al multiplicarlo por el primer sumando del polinomio Q(x) = 2x^2 + x - 1 el resultado sea exactamente igual al primer sumando del polinomio P(x) = 8x^3 - 6x^2 - 2, en este caso el polinomio que estamos buscando es 4x y lo escribimos de la siguiente forma

División de Polinomios | totumat.com

El siguiente paso será multiplicar el polinomio Q(x) = 2x^2 + x - 1 por x y el resultado se lo restamos al polinomio P(x) = 8x^3 - 6x^2 - 2 de la siguiente forma

División de Polinomios | totumat.com

Notamos que el grado del polinomio en el resto es menor que el grado del polinomio Q(x), por lo tanto, el siguiente paso será buscar un polinomio tal que al multiplicarlo por el primer sumando del polinomio Q(x) = 2x^2 + x - 1 el resultado sea exactamente igual al primer sumando del polinomio en el resto, de decir, el polinomio -10x^2 + 4x.

En este caso el polinomio que estamos buscando es -5 y lo multiplicamos por el polinomio Q(x) = 2x^2 + x - 1; el resultado se lo restamos al polinomio -10x^2 + 4x de la siguiente forma

División de Polinomios | totumat.com

Notamos que el grado del polinomio en el resto es menor que el grado del polinomio Q(x), Por lo tanto, concluimos que

8x^3 - 6x^2 - 2 = (4x-5) \cdot (2x^2 + x - 1) + 9x-7

Bosquejo de Polinomios

Anthonny Arias GarcíaDeja un comentario

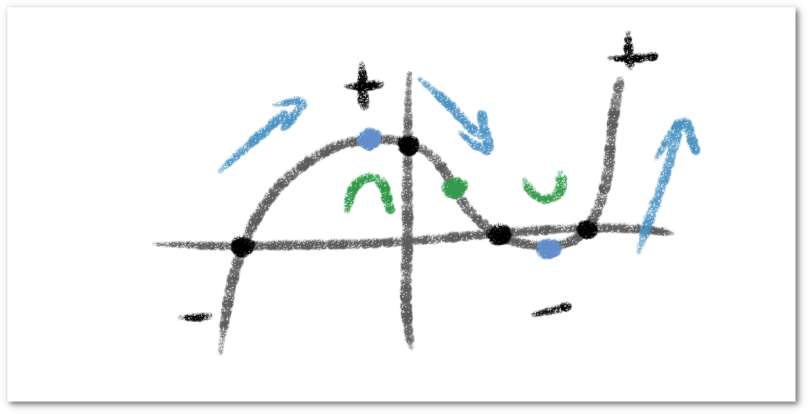
Si se sabe interpretar de forma correcta la información que se obtiene de las derivadas de una función se puede hacer bosquejo de un polinomio sin necesidad de extenderse mucho en los cálculos, sin embargo, definamos una serie de pasos que facilite el flujo de la información que vamos obteniendo del polinomio para poder apreciar su comportamiento general. Si P(x) un polinomio, entonces

  1. Calculamos los puntos de corte con los ejes y estudiamos su positividad (intervalos en los que es positiva o negativa).
  2. Calculamos los puntos críticos y determinamos su monotonía (intervalos en los que crece o decrece).
  3. Calculamos los puntos de inflexión y determinamos su concavidad (intervalos en los que es convexa o cóncava).
  4. Calculamos las imágenes de los puntos de los puntos críticos y de inflexión.
  5. Esbozar la gráfica.

De esta forma, aunque es un proceso extenso, se observa con claridad el comportamiento de la función en cada intervalo de la recta real estudiando la función, su primera derivada y su segunda derivada. Veamos con algunos ejemplos como hacer estos bosquejos.

También pudiera interesarte

Anuncios

Ejemplos

Ejemplo 1

Haga un bosquejo del polinomio P(x) = x^2 + 5x +6

Primer Paso: Puntos de Corte y Positividad.

Para determinar el punto de corte del polinomio con el Eje Y, calculamos el valor del polinomio cuando x=0, esto es

P(0) = (0)^2 + 5(0) +6 = 6

Para determinar los puntos de corte del polinomio con el Eje X, calculamos el valor de la variable x cuando P(x)=0, esto es,

x^2 + 5x +6 = 0 \Longrightarrow (x+2)(x+3)=0

Entonces, los puntos de corte del polinomio con el Eje X son x=-2 y x=-3. Así, podemos estudiar la positividad del polinomio haciendo una tabla de análisis de signo:

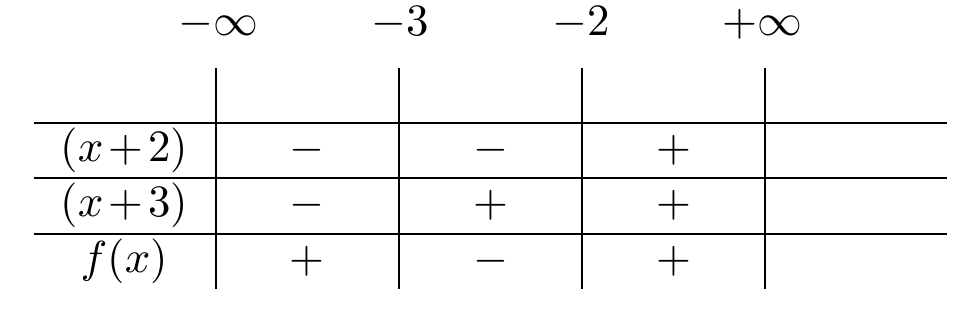
De esta forma, concluimos que el polinomio P(x)

  • Está por encima del Eje X en los intervalos (-\infty,-3) y (-2,+\infty).
  • Está por debajo del Eje X en el intervalo (-3,-2).

Segundo Paso: Puntos Críticos y Monotonía.

Para determinar los puntos críticos del polinomio P(x) calculamos su primera derivada y obtenemos P'(x) = 2x+5. Calculamos los valores para los cuales P'(x)=0, esto es,

2x+5 = 0 \Longrightarrow x = -\frac{5}{2}

Entonces, el punto crítico del polinomio es x=-\frac{5}{2}. Así, podemos estudiar la monotonía del polinomio haciendo una tabla de análisis de signo:

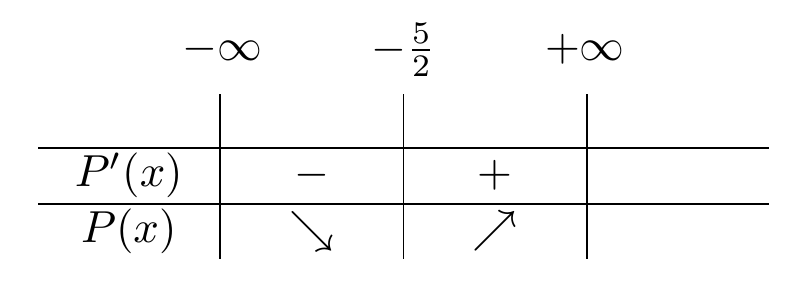
De esta forma, concluimos que el polinomio P(x)

  • Es decreciente en el intervalo (-\infty,-\frac{5}{2}),
  • Es creciente en el intervalo (-\frac{5}{2},+\infty).
  • Alcanza un mínimo local en x=-\frac{5}{2}.
Anuncios

Tercer Paso: Puntos de Inflexión y Concavidad.

Para determinar los puntos de inflexión del polinomio P(x) calculamos su segunda derivada y obtenemos P''(x) = 2. Concluyendo inmediatamente que nunca es igual a cero, entonces no tiene puntos de inflexión. Aunque la conclusión es clara, haremos una tabla de análisis de signo para ilustrar lo que ocurre.

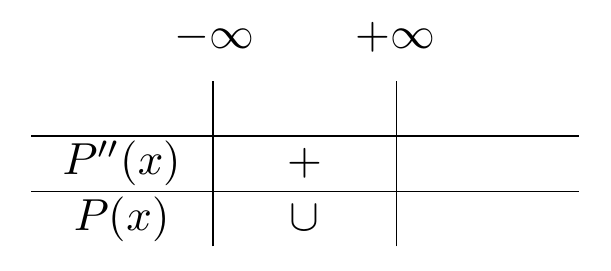
De esta forma, concluimos que el polinomio P(x)

  • Es convexo en todo su dominio.

Cuarto Paso: Imágenes.

  • P(-\frac{5}{2}) =\left( -\frac{5}{2} \right)^2 + 5 \left( -\frac{5}{2} \right) + 6 = -\frac{1}{4} = -0.25

Quinto Paso: Graficar.

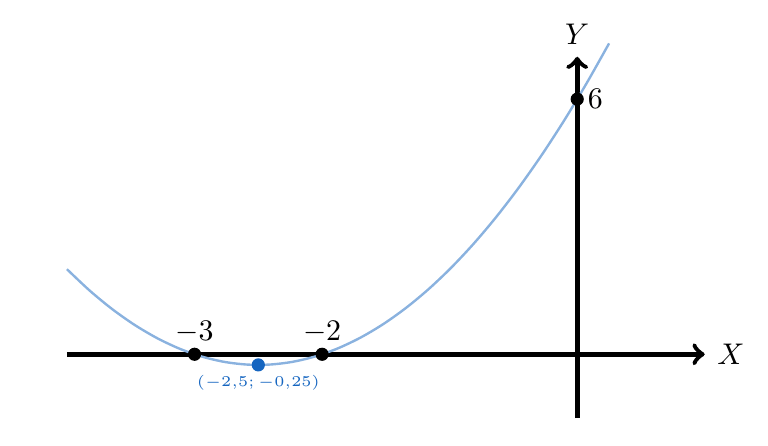
Puntos de Corte.

Puntos Críticos.

Anuncios

Ejemplo 2

Haga un bosquejo del polinomio P(x) = x^3 - 2x^2 -x +2

Primer Paso: Puntos de Corte y Positividad.

Para determinar el punto de corte del polinomio con el Eje Y, calculamos el valor del polinomio cuando x=0, esto es

P(0) = (0)^3 - 2(0)^2 -(0) +2 = 2

Para determinar los puntos de corte del polinomio con el Eje X, calculamos el valor de la variable x cuando P(x)=0, esto es,

x^3 - 2x^2 -x +2 = 0

Considerando que este polinomio es de grado tres, el método que usaremos para calcular sus raíces será el Método de Ruffini. Entonces, consideramos sus coeficientes de la siguiente manera

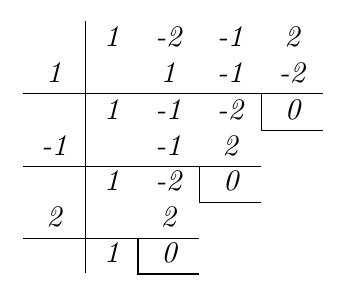
Entonces, los puntos de corte del polinomio con el Eje X son x=1, x=-1 y x=2. Así, podemos factorizar el polinomio como P(x)=(x-1)(x+1)(x-2) y estudiar su positividad haciendo una tabla de análisis de signo:

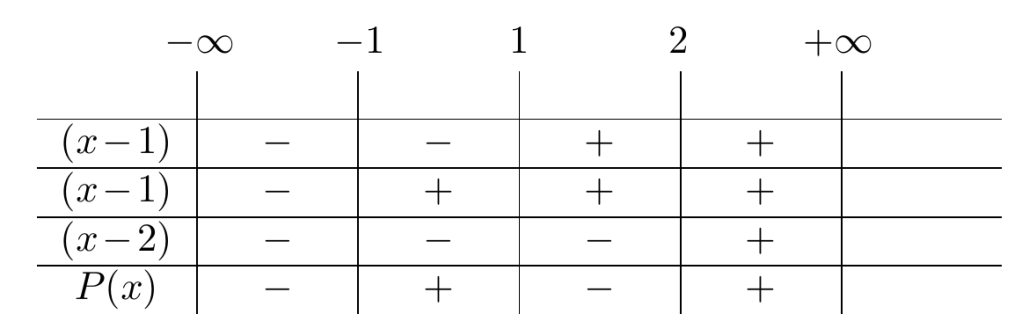
De esta forma, concluimos que el polinomio P(x)

  • Está por encima del Eje X en los intervalos (-1,1) y (2,+\infty)
  • Está por debajo del Eje X en los intervalos (-\infty,-1) y (1,2).

Segundo Paso: Puntos Críticos y Monotonía.

Para determinar los puntos críticos del polinomio P(x) calculamos su primera derivada y obtenemos P'(x) = 3x^2 - 4x -1. Calculamos los valores para los cuales P'(x)=0. Considerando que este polinomio es de segundo grado, el método que usaremos para calcular sus raíces será el Método del Discriminante.

Identificamos los coeficientes del polinomio como a=3, b=-4 y c=-1 y aplicamos la fórmula del discriminante

x = \dfrac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a}

= \dfrac{-(-4) \pm \sqrt{(-4)^2-4 \cdot 3 \cdot (-1)}}{2 \cdot 3}

= \dfrac{4 \pm \sqrt{16+12}}{6}

= \dfrac{4 \pm \sqrt{28}}{6}

= \dfrac{2 \pm \sqrt{7}}{3}

x_1 = \dfrac{2 + \sqrt{7}}{3} \approx 1.54858

x_2 = \dfrac{2 - \sqrt{7}}{3} \approx -0.21525

Entonces, los puntos críticos del polinomio son x=\dfrac{2 + \sqrt{7}}{3} y x=\dfrac{2 - \sqrt{7}}{3}. Así, podemos factorizar la primera derivada del polinomio como P'(x)=3\left( x - \frac{2 + \sqrt{7}}{3} \right)\left( x + \frac{2 + \sqrt{7}}{3} \right) y estudiar la monotonía del polinomio haciendo una tabla de análisis de signo:

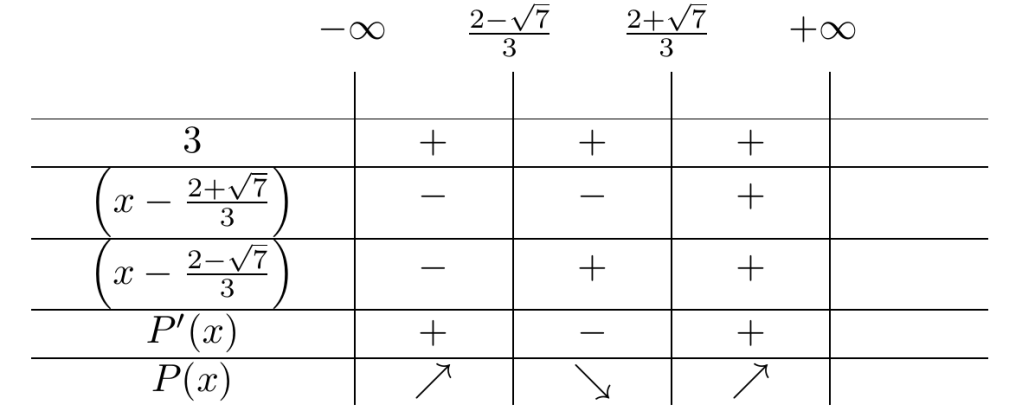
De esta forma, concluimos que el polinomio P(x)

  • Es creciente en los intervalos \left(-\infty,\frac{2 - \sqrt{7}}{3}\right) y \left(\frac{2 + \sqrt{7}}{3},+\infty\right).
  • Es decreciente en el intervalo \left(\frac{2 - \sqrt{7}}{3},\frac{2 + \sqrt{7}}{3}\right).
  • Alcanza un máximo local en x=\frac{2 - \sqrt{7}}{3}.
  • Alcanza un mínimo local en x=\frac{2 + \sqrt{7}}{3}.
Anuncios

Tercer Paso: Puntos de Inflexión y Concavidad.

Para determinar los puntos de inflexión del polinomio P(x) calculamos su segunda derivada y obtenemos P''(x) = 6x-4. Calculamos los valores para los cuales P''(x)=0. Considerando que este polinomio lineal, el método que usaremos para calcular sus raíces será un simple despeje de la siguiente manera

6x-4 = 0 \Longrightarrow 6x = 4 \Longrightarrow x = \frac{4}{6} \Longrightarrow x = \frac{2}{3}

Entonces nuestro posible punto de inflexión es x=\frac{2}{3}, y estudiamos la concavidad del polinomio haciendo una tabla de análisis de signo:

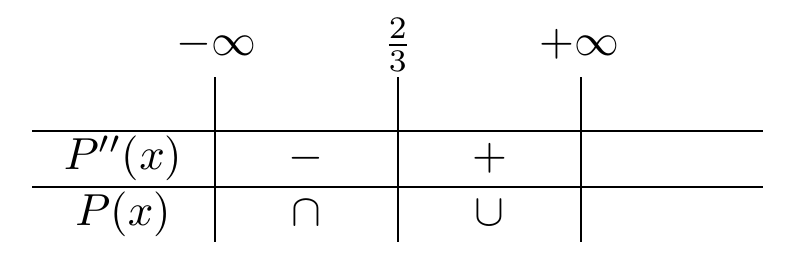
De esta forma, concluimos que el polinomio P(x)

  • Es cóncavo en el intervalo (-\infty,\frac{2}{3}).
  • Es convexo en el intervalo (\frac{2}{3},+\infty).
  • Alcanza un punto de inflexión en x=\frac{2}{3}.

Cuarto Paso: Imágenes.

  • P\left(\frac{2 + \sqrt{7}}{3} \right) = \left(\frac{2 + \sqrt{7}}{3} \right)^3 - 2\left(\frac{2 + \sqrt{7}}{3} \right)^2 -\left(\frac{2 + \sqrt{7}}{3} \right) +2 \approx -0.63113
  • P\left(\frac{2 - \sqrt{7}}{3} \right) = \left(\frac{2 - \sqrt{7}}{3} \right)^3 - 2\left(\frac{2 - \sqrt{7}}{3} \right)^2 -\left(\frac{2 - \sqrt{7}}{3} \right) +2 \approx 2.11261
  • P\left(\frac{2}{3} \right) = \left(\frac{2}{3} \right)^3 - 2\left(\frac{2}{3} \right)^2 -\left(\frac{2}{3} \right) +2 \approx 0.740741

Quinto Paso: Graficar.

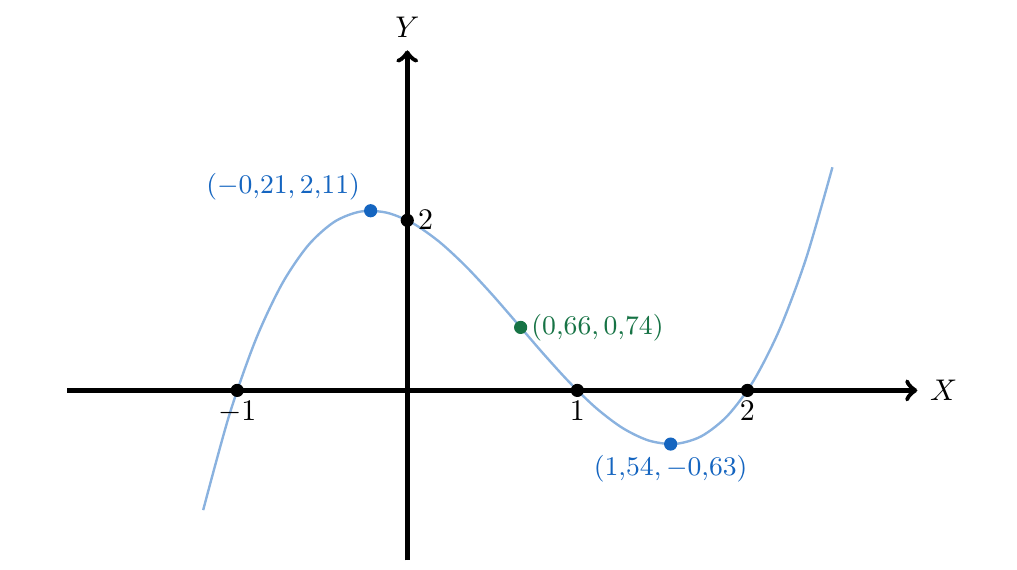
Puntos de Corte.

Puntos Críticos.

Puntos de Inflexión.

Inecuaciones Polinómicas y la Tabla de Análisis de Signos

Anthonny Arias García4 comentarios
  1. ¿Qué es una inecuación polinómica?
  2. La Tabla de Análisis de Signos
    1. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2

Para calcular la solución de una inecuación lineal basta con usar las técnicas despeje que normalmente se usan para calcular una ecuación lineal, y como resultado, generalmente obtenemos un conjunto infinito de número.

Para calcular la solución de una inecuación cuadrática, factorizamos el polinomio cuadrático y recurrimos a la Ley de los Signos, para analizar los dos casos posibles a partir del signo de cada factor involucrado.

Para calcular la solución de una inecuación polinómica, también recurriremos a la factorización de polinomios, sin embargo, el análisis de cada caso puede ser engorroso pues a medida que aumentan los factores, también aumentan los casos. Es por esto, que recurriremos a una herramienta que nos permita analizar el signo del polinomio de una forma global.

También pudiera interesarte

Anuncios

¿Qué es una inecuación polinómica?

Una inecuación polinómica, es una inecuación que involucra a una una potencia de la variable x. Formalmente, si consideramos un conjunto de n números reales a_n, a_{n-1}, \ldots, a_2, a_1, a_0, definimos una inecuación polinómica como una inecuación que se puede expresar de la siguiente forma:

a_n x^n + a_{n-1} x^{n-1} + ... + a_2 x^2 + a_1 x + a_0 > 0

Donde «>» representa cualquier desigualdad >, \geq, < ó \leq.

Si definimos P(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_2 x^2 + a_1 x + a_0, entonces podemos expresar una inecuación polinómica de la siguiente forma:

P(x) > 0

La Tabla de Análisis de Signos

La técnica que usaremos para calcular la solución de este tipo de inecuaciones, consiste en calcular las raíces del polinomio P(x), factorizarlo a partir de sus raíces y posteriormente, analizar el signo de cada factor a lo largo de cada número real, es decir, para qué valores de x cada factor es positivo o negativo.

En los siguientes ejemplos explicaremos cómo usar una Tabla de Análisis de Signos o simplemente Tabla de Signos (coloquialmente conocida como el método del cementerio o método de las cruces) para calcular la solución de inecuaciones polinómicas.

La tabla de análisis de signos está basada en el Teorema de Sturm, que en términos llanos, permite determinar la cantidad de raíces de un polinomio en un intervalo a partir de la cantidad de veces que varía el signo de dicho polinomio en dicho intervalo.

Anuncios
Anuncios
Anuncios

Ejemplos

Ejemplo 1

Calcule los valores de x que satisfacen la siguiente desigualdad:

x^3 + 2x^2 - x - 2 > 0

El primero paso será calcular las raíces del polinomio P(x) = x^3 + 2x^2 - x - 2, Esto lo haremos usando el Método de Ruffini de la siguiente forma:

Método de Ruffini | totumat.com

Por lo tanto, concluimos que las raíces del polinomio P(x) son x_1=1, x_2=-1 y x_3=-2.

A partir de dichas raíces, podemos factorizar el polinomio como sigue:

P(x) = (x-1)(x-(-1))(x-(-2)) = (x-1)(x+1)(x+2)

Nuestro propósito será el de determinar el signo de cada uno de los factores involucrados entre los intervalos (-\infty,-2), (-2,-1), (-1,1) y (1,+\infty). Para esto disponemos en la recta real cada una de las raíces del polinomio, -\infty y +\infty de forma ordenada:

Construcción de una Tabla de Signos | totumat.com

Debajo de cada una de las raíces del polinomio, -\infty y +\infty se trazan rectas verticales; y además se trazan cuatro renglones, siendo uno para cada factor y uno adicional para el polinomio P(x):

Construcción de una Tabla de Signos | totumat.com

En estos renglones se disponen los factores (x-1), (x+1), (x+2) y el polinomio P(x), de la siguiente forma:

Construcción de una Tabla de Signos | totumat.com

Ubicamos en la tabla valor de x para el cual se anula el primer factor, es decir, el valor de x para el cual x-1 = 0. Este valor es 1 y concluimos lo siguiente:

  • Para los valores de x menores que 1, el factor (x-1) es negativo.
  • Para los valores de x mayores que 1, el factor (x-1) es positivo.
Construcción de una Tabla de Signos | totumat.com

Ubicamos en la tabla valor de x para el cual se anula el segundo factor, es decir, el valor de x para el cual x+1 = 0. Este valor es -1 y concluimos lo siguiente:

  • Para los valores de x menores que -1, el factor (x-1) es negativo.
  • Para los valores de x mayores que -1, el factor (x-1) es positivo.
Construcción de una Tabla de Signos | totumat.com

Ubicamos en la tabla valor de x para el cual se anula el tercer factor, es decir, el valor de x para el cual x+2 = 0. Este valor es -2 y concluimos lo siguiente:

  • Para los valores de x menores que -2, el factor (x-1) es negativo.
  • Para los valores de x mayores que -2, el factor (x-1) es positivo.
Construcción de una Tabla de Signos | totumat.com

Para cada intervalo (-\infty,-2), (-2,-1), (-1,1) y (1,+\infty) el signo de P(X) está definido por el producto de los factores (x-1), (x+1) y (x+2). De esta forma, multiplicamos los signos de los factores de cada columna:

  • En la primera columna (-) \cdot (-) \cdot (-) = -
  • En la segunda columna (-) \cdot (-) \cdot (+) = +
  • En la tercera columna (-) \cdot (+) \cdot (+) = -
  • En la cuarta columna (+) \cdot (+) \cdot (+) = +

Por lo tanto, nuestra Tabla de Análisis de Signos queda expresada de la siguiente forma:

Construcción de una Tabla de Signos | totumat.com

Finalmente, concluimos que la desigualdad planteada en x^3 + 2x^2 - x - 2 > 0 se satisface para los valores de x que pertenecen al intervalo (-2,-1) o al intervalo (1,+\infty), entonces la solución general de la inecuación está definida por la siguiente unión de intervalo:

(-2,-1) \cup (1,+\infty)

Anuncios
Anuncios
Anuncios

Ejemplo 2

Calcule los valores de x que satisfacen la siguiente desigualdad:

-2x^3 - 10x^2 + 4x + 48 \leq 0

Lo primero que debemos notar es que podemos sacar -2 como un factor en el polinomio P(x) = -2x^3 - 10x^2 + 4x + 48. De esta forma, obtenemos la siguiente expresión:

-2 \cdot (x^3 + 5x^2 - 2x - 24) \leq 0


El siguiente paso será calcular las raíces del polinomio x^3 + 5x^2 - 2x - 24, Esto lo haremos usando el Método de Ruffini, como sigue:

Método de Ruffini | totumat.com

Por lo tanto, concluimos que las raíces del polinomio P(x) son x_1=2, x_2=-3 y x_3=-4.

A partir de dichas raíces, podemos factorizar el polinomio como sigue:

P(x) = -2(x-2)(x-(-3))(x-(-4)) = -2(x-2)(x+3)(x+4)

Nuestro propósito será el de determinar el signo de cada uno de los factores involucrados entre los intervalos (-\infty,-4], [-4,-3], [-3,2] y [2,+\infty]. Para esto disponemos en la recta real cada una de las raíces del polinomio, -\infty y +\infty de forma ordenada.

Es importante tomar en cuenta que -2 es un factor negativo constante, así, nuestra tabla de análisis de signo quedará expresada de la siguiente forma:

Construcción de una Tabla de Signos | totumat.com

Finalmente, concluimos que la desigualdad planteada en la inecuación -2x^3 - 10x^2 + 4x + 48 \leq 0 se satisface para los valores de x que pertenecen al intervalo [-4,-3] o al intervalo [2,+\infty), entonces la solución general de la ecuación es:

[-4,-3] \cup [2,+\infty)

Memes relacionados

Cuando le llamas «Tabla de Análisis de Signos» en vez de «el método del cementerio».