Una vez que hemos definido la ecuación canónica de la recta, es posible, al estudiar una recta en particular, determinar la ecuación que la define a partir de cierta información, pero, ¿cómo?
Si consideramos un punto en el plano, es fácil intuir que por ese punto pasan infinitas rectas, sin embargo, al fijar un ángulo de inclinación, a través de dicho punto, sólo pasará una única recta que tenga ese ángulo de inclinación. De esta idea partiremos para determinar la ecuación canónica de una recta.
También pudiera interesarte
La fórmula de la Ecuación Punto-Pendiente
Si una recta pasa por un punto en el plano cartesiano, digamos y su ángulo de inclinación induce una pendiente de
, podemos determinar la ecuación que la define planteando la siguiente fórmula:
A esta fórmula la llamaremos ecuación punto-pendiente y a partir de esta igualdad, podemos determinar la ecuación canónica de dicha recta, simplemente despejando la variable .
Veamos con algunos ejemplos como determinar la ecuación canónica de una recta contando con estos dos elementos.
Ejemplos
Ejemplo 1
Calcule la ecuación de la recta que pasa por el punto y tiene pendiente
.
Concluimos entonces que la ecuación de la recta que estamos buscando es , que es precisamente la recta identidad y su gráfica es la siguiente:
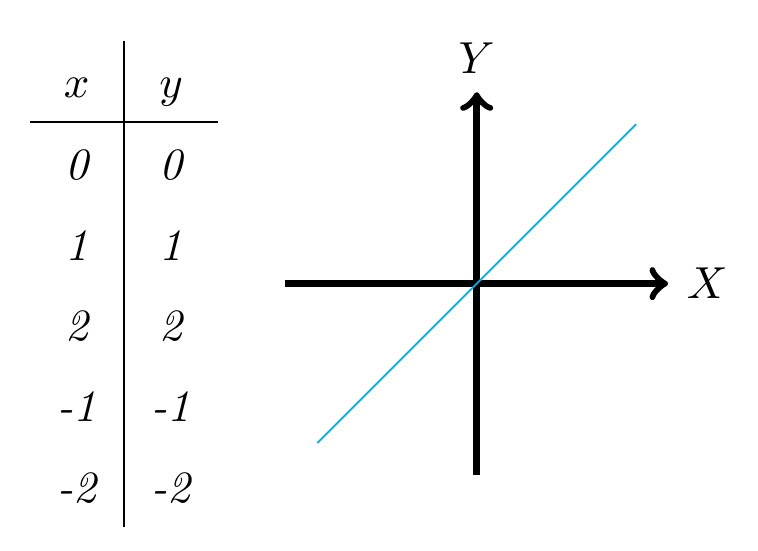
Ejemplo 2
Calcule la ecuación de la recta que pasa por el punto y tiene pendiente
.
Concluimos entonces que la ecuación de la recta que estamos buscando es y para determinar su gráfica, en vez de calcular todos los puntos por donde ésta pasa, podemos simplemente considerar dos puntos ya que por cualquier par de puntos pasa una única recta.
Particularmente consideraremos los puntos de corte de la recta con los ejes, es decir, los puntos de la forma y
. Entonces,
Es decir, el punto de corte con el Eje Y es
Es decir, el punto de corte con el Eje X es
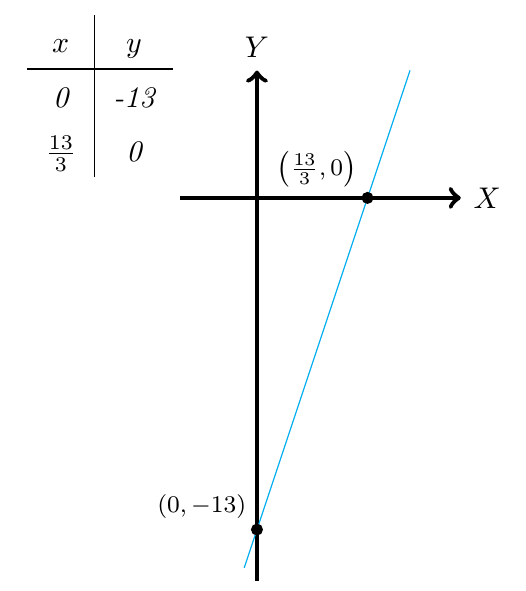
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 3
Calcule la ecuación de la recta que pasa por el punto y tiene pendiente
.
Concluimos entonces que la ecuación de la recta que estamos buscando es y para determinar su gráfica, en vez de calcular todos los puntos por donde ésta pasa, podemos simplemente considerar dos puntos ya que por cualquier par de puntos pasa una única recta.
Particularmente consideraremos los puntos de corte de la recta con los ejes, es decir, los puntos de la forma y
. Entonces,
Es decir, el punto de corte con el Eje Y es
Es decir, el punto de corte con el Eje X es
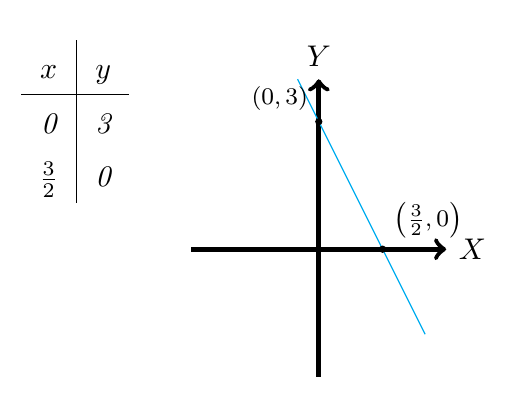
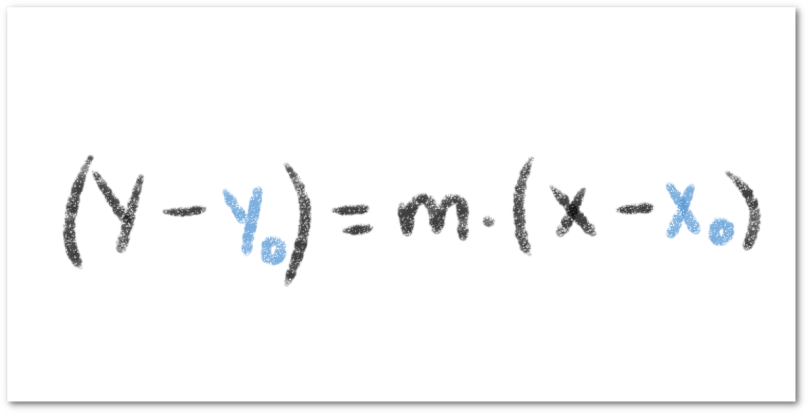

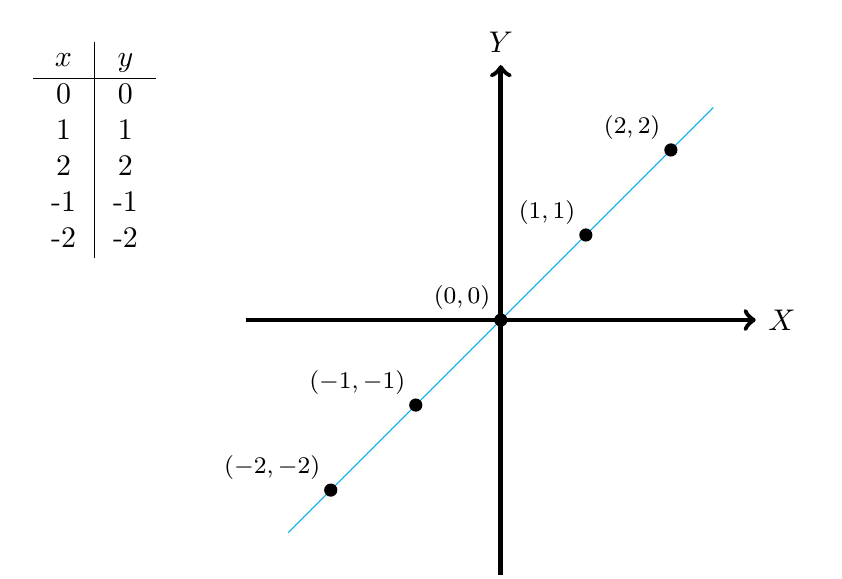

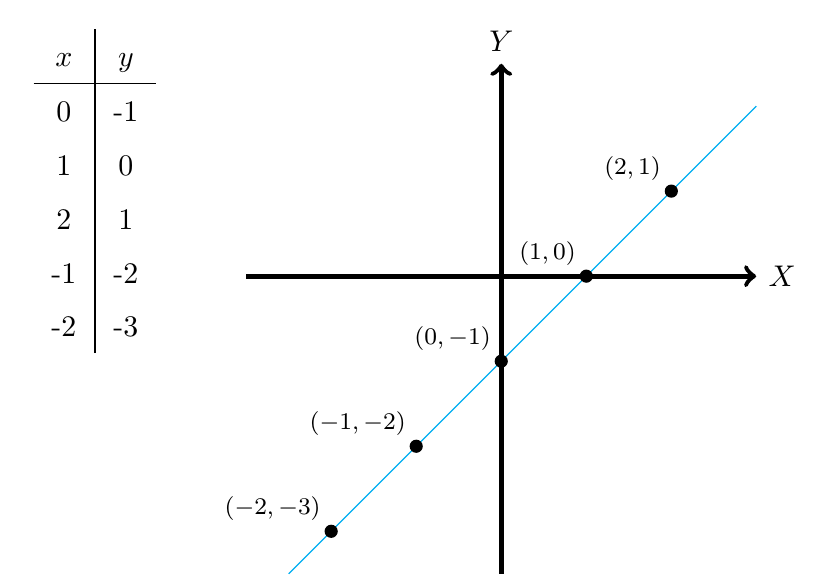
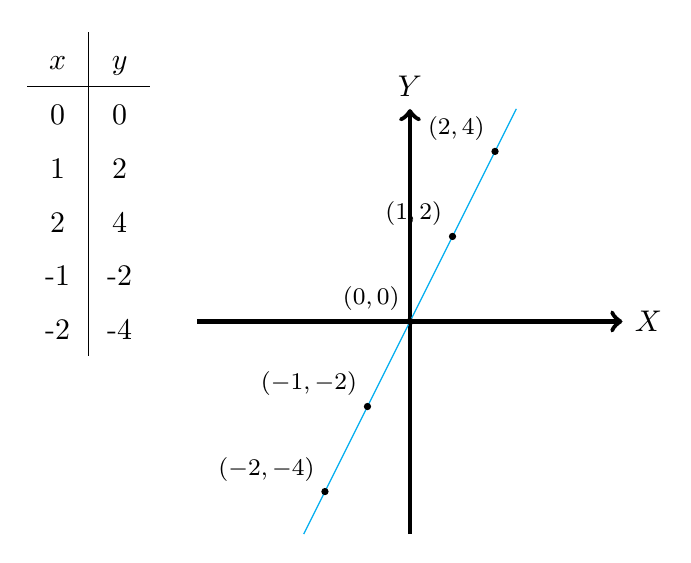
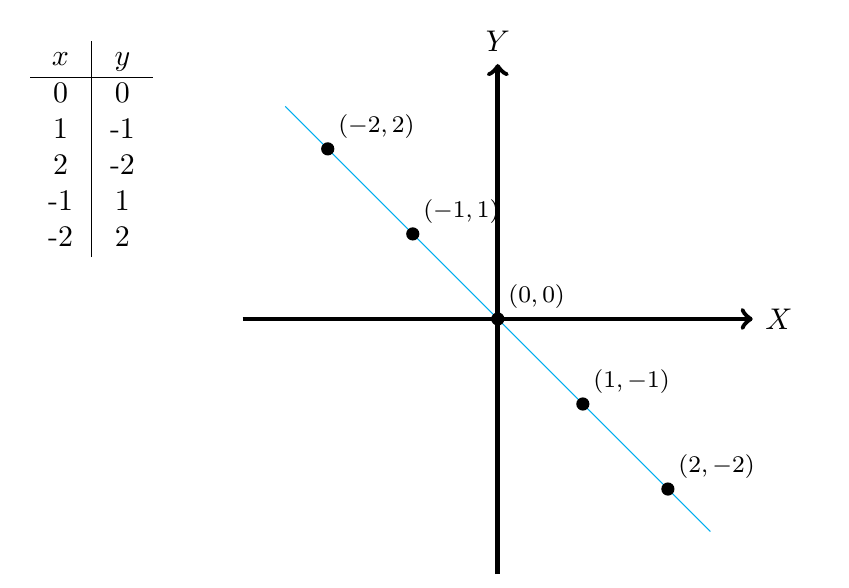
Debe estar conectado para enviar un comentario.