Ejercicios Propuestos - Ecuaciones Diferenciales

Ejercicios Propuestos – Modelo de Harrod-Domar

06.04.202106.04.2021 Anthonny Arias-GarcíaDeja un comentario

Tomando en cuenta que

$I'(t)=s\rho I(t)$

Determine la trayectoria de la inversión que mantendrá la economía en equilibrio todo el tiempo considerando la porción de la producción agregada al capital, la tasa de capacidad-capital y la tasa de inversión inicial dadas en cada ejercicio. Adicionalmente, calcule las trayectorias de capital y flujo de ingresos.

La propensión marginal al ahorro es del 9%, la tasa de capacidad-capital es 0.5281, la inversión inicial es 175.18 y el capital inicial es 17518. Calcule el valor de cada una de estas trayectorias en el año 9.

La propensión marginal al ahorro es del 13%, la tasa de capacidad-capital es 0.8791, la inversión inicial es 143.1 y el capital inicial es 14310. Calcule el valor de cada una de estas trayectorias en el año 10.

La propensión marginal al ahorro es del 6%, la tasa de capacidad-capital es 0.4118, la inversión inicial es 96.79 y el capital inicial es 9679. Calcule el valor de cada una de estas trayectorias en el año 8.

La propensión marginal al ahorro es del 1%, la tasa de capacidad-capital es 0.7937, la inversión inicial es 342.7 y el capital inicial es 34270. Calcule el valor de cada una de estas trayectorias en el año 4.

La propensión marginal al ahorro es del 2%, la tasa de capacidad-capital es 0.2471, la inversión inicial es 252.66 y el capital inicial es 25266. Calcule el valor de cada una de estas trayectorias en el año 3.

La propensión marginal al ahorro es del 19%, la tasa de capacidad-capital es 0.0943, la inversión inicial es 147.08 y el capital inicial es 14708. Calcule el valor de cada una de estas trayectorias en el año 4.

La propensión marginal al ahorro es del 10%, la tasa de capacidad-capital es 0.1923, la inversión inicial es 283.16 y el capital inicial es 28316. Calcule el valor de cada una de estas trayectorias en el año 8.

La propensión marginal al ahorro es del 10%, la tasa de capacidad-capital es 0.1667, la inversión inicial es 33.93 y el capital inicial es 3393. Calcule el valor de cada una de estas trayectorias en el año 10.

También pudiera interesarte

Ejercicios Propuestos – Modelo de Crecimiento y Decrecimiento

06.04.202107.12.2022 Anthonny Arias-GarcíaDeja un comentario

En lo siguientes ejercicios, considere el tamaño inicial de la población $P_0$ para determinar el tamaño de la población en el tiempo $t$ indicado sabiendo que la población de una comunidad crece con una razón proporcional al número de personas presentes en el tiempo $t$ .

El tamaño inicial de la población es $P_0=9042$ , sabiendo que en el año $t=5$ la población se ha duplicado. Calcule el tamaño de la población en el año 32. Calcule además el tiempo en que esta población se ha triplicado.

El tamaño inicial de la población es $P_0=8904$ , sabiendo que en el año $t=15$ la población se ha duplicado. Calcule el tamaño de la población en el año 48. Calcule además el tiempo en que esta población se ha sextuplicado.

El tamaño inicial de la población es $P_0=7013$ , sabiendo que en el año $t=1$ la población se ha duplicado. Calcule el tamaño de la población en el año 31. Calcule además el tiempo en que esta población se ha cuadruplicado.

El tamaño inicial de la población es $P_0=5641$ , sabiendo que en el año $t=1$ la población se ha duplicado. Calcule el tamaño de la población en el año 46. Calcule además el tiempo en que esta población se ha sextuplicado.

El tamaño inicial de la población es $P_0=6632$ , sabiendo que en el año $t=18$ la población se ha duplicado. Calcule el tamaño de la población en el año 45. Calcule además el tiempo en que esta población se ha cuadruplicado.

El tamaño inicial de la población es $P_0=3786$ , sabiendo que en el año $t=4$ la población se ha duplicado. Calcule el tamaño de la población en el año 48. Calcule además el tiempo en que esta población se ha triplicado.

El tamaño inicial de la población es $P_0=4963$ , sabiendo que en el año $t=15$ la población se ha duplicado. Calcule el tamaño de la población en el año 40. Calcule además el tiempo en que esta población se ha cuadruplicado.

El tamaño inicial de la población es $P_0=2937$ , sabiendo que en el año $t=15$ la población se ha duplicado. Calcule el tamaño de la población en el año 47. Calcule además el tiempo en que esta población se ha quintuplicado.

También pudiera interesarte

Excedente de los Consumidores y de los Productores – Caso lineal

06.12.202007.12.2022 Anthonny Arias-GarcíaDeja un comentario

Al estudiar el mercado, es notorio que los productores siempre querrán vender a un precio elevado y los consumidores siempre querrán comprar a un precio bajo. El punto de equilibrio del mercado permite establecer un consenso entre las dos partes, sin embargo, ¿qué tanto beneficia este consenso a las partes?

También pudiera interesarte

Excedente de los Consumidores

Suponga que usted va al supermercado con el objetivo de comprar un producto y que cuando lo va a pagar, recibe la grata sorpresa de que está más barato de lo que usted pensaba, esta situación tiene una interpretación formal. Si observamos la recta de demanda de un determinado artículo, podemos notar que si se fija el precio de cada unidad en 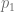$p_1$ Perolitos (Ps.), los consumidores estarán dispuestos a comprar 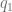$q_1$ unidades de dicho artículo.

Sin embargo, una vez que se ha fijado el punto de equilibrio 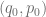$(q_0,p_0)$ Ps., podemos notar que aquellos consumidores que están dispuestos a comprar 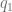$q_1$ unidades cuando el precio se había fijado en 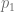$p_1$ Ps., ahora comprarán las mismas 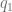$q_1$ unidades pagando cada unidad en un menor precio de 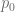$p_0$ Ps.

De esta forma, si un consumidor pensaba gastar 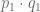$p_1 \cdot q_1$ Ps. (precio por unidad multiplicado por la cantidad adquirida), una vez que se ha fijado el precio de equilibrio, gastará $p_0 \cdot q_1$ Ps. Esto genera un beneficio para los consumidores, y a partir de este hecho surge la siguiente pregunta: ¿es posible cuantificar este beneficio?

Para responder a esta pregunta, supongamos que la cantidad de unidades que los consumidores piensan comprar no es fija sino que es una gama representada por un rango de unidades comprendidas entre ninguna unidad y la cantidad 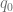$q_0$ , fijada por el punto de equilibrio. El gasto que pagarían originalmente, está representado por el área que está debajo de la recta de demanda de la siguiente forma,

Pero como al final los consumidores están pagando un precio de 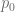$p_0$ Ps. por cada unidad, el beneficio generado al fijar el equilibrio, está representado por el área que está debajo de la recta de demanda y por encima del precio de equilibrio de la siguiente forma,

El área que representa el beneficio para los consumidores una vez que se ha fijado el precio de equilibrio se llama Excedente de los Consumidores o Superávit de los Consumidores, y lo podemos medir calculando el área del triángulo que genera la recta de demanda, la recta del precio de equilibrio y el Eje P.

Recordemos que el área de un triángulo se calcula multiplicando la longitud de la base por la longitud de la altura, dividido entre dos. La longitud de la base está dada por 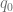$q_0$ y si llamamos $D$ al punto de intersección de la recta de demanda con el Eje P, su altura está dada por $D - p_0$ .

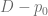Por lo tanto calculamos el excedente de los consumidores planteando la siguiente fórmula:

$E.C. \ = \ \frac{q_0 \cdot (D - p_0)}{2}$

Anuncios

Excedente de los Productores

Suponga que usted es productor de un artículo pero luego de estudiar los costos y un posible precio de venta para recibir unos ingresos aceptables, recibe la grata sorpresa de que puede fijar un precio por encima de lo que usted pensaba, esta situación tiene una interpretación formal. Si observamos la recta de oferta de un determinado artículo, podemos notar que los productores estarán dispuestos a ofertar 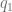$q_1$ unidades de dicho artículo si se fija el precio de cada unidad en 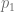$p_1$ Perolitos (Ps.),

Sin embargo, una vez que se ha fijado el punto de equilibrio 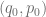$(q_0,p_0)$ Ps., podemos notar que aquellos productores que están dispuestos a ofertar 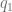$q_1$ unidades cuando el precio se había fijado en 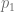$p_1$ Ps., ahora ofertarán las mismas 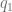$q_1$ unidades vendiendo cada unidad en un mayor precio de 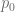$p_0$ Ps.

De esta forma, si un productor pensaba recibir 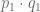$p_1 \cdot q_1$ Ps. (precio por unidad multiplicado por la cantidad adquirida), una vez que se ha fijado el precio de equilibrio, recibir $p_0 \cdot q_1$ Ps. Esto genera un beneficio para los productores, y a partir de este hecho surge la siguiente pregunta: ¿es posible cuantificar este beneficio?

Para responder a esta pregunta, supongamos que la cantidad de unidades que los productores piensan ofertar no es fija sino que es una gama representada por un rango de unidades comprendidas entre ninguna unidad y la cantidad 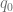$q_0$ , fijada por el punto de equilibrio. Los ingresos que recibirían originalmente, están representado por el área que está debajo de la recta de oferta de la siguiente forma,

Pero como al final los productores están vendiendo a un precio de 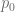$p_0$ Ps. por cada unidad, el beneficio generado al fijar el equilibrio, está representado por el área que está debajo del precio de equilibrio y por encima de la recta de oferta de la siguiente forma,

El área que representa el beneficio para los productores una vez que se ha fijado el precio de equilibrio se llama Excedente de los Productores o Superávit de los Productores, y lo podemos medir calculando el área del triángulo que genera la recta de oferta, la recta del precio de equilibrio y el Eje P.

Recordemos que el área de un triángulo se calcula multiplicando la longitud de la base por la longitud de la altura, dividido entre dos. La longitud de la base está dada por 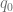$q_0$ y si llamamos 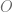$O$ al punto de intersección de la recta de demanda con el Eje P, su altura está dada por $p_0 - O$ .

Por lo tanto calculamos el excedente de los productores planteando la siguiente fórmula:

$E.P. \ = \ \frac{q_0 \cdot (p_0 - O)}{2}$

Consideremos en los siguientes ejemplos cómo calcular el excedente de los consumidores y el excedente de los fabricantes considerando la curva de demanda y la curva de oferta del mercado.

Anuncios

Ejemplos

Ejemplo 1

Considerando la ecuación de demanda $p = -\frac{67}{100}q +126$ y la ecuación de oferta $p = \frac{13}{25}q +36$ , calcule el punto de equilibrio del mercado; posteriormente calcule el excedente de los consumidores y el excedente de los fabricantes.

Para calcular el punto de equilibrio del mercado debemos igualar las expresiones que definen ambas rectas y luego despejamos la variable 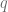$q$ .

$-\frac{67}{100}q +126 = \frac{13}{25}q+36$

$\Rightarrow \ -\frac{67}{100}q - \frac{13}{25}q = 36-126$

$\Rightarrow \ -\frac{119}{100}q = -90$

$\Rightarrow \ q = \frac{9000}{119}$

Una vez calculado el valor de 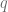$q$ , lo sustituimos en la recta de nuestra preferencia y calculamos el valor de 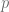$p$ . Sustituyamos entonces el valor 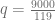$q=\frac{9000}{119}$ en la ecuación de demanda.

$p = \ -\frac{67}{100} \cdot \left( \frac{9000}{119} \right) + 126$

$= \ -\frac{6030}{119} + 126$

$= \ \frac{8964}{119}$

Por lo tanto, el punto de equilibrio del mercado $\left( \frac{9000}{119} , \frac{8964}{119} \right)$ . Grafiquemos ahora el punto de equilibrio del mercado e identifiquemos las áreas que definen los excedentes.

Excedente de los Consumidores y de los Productores | totumat.com

Calculamos el Excedente de los Consumidores:

$\frac{q_0 \cdot (D - p_0)}{2} = \frac{ \frac{9000}{119} \cdot \left( 126 - \frac{8964}{119} \right)}{2} = \frac{27135000}{14161} \approx 1916.18$

Calculamos el Excedente de los Fabricantes:

$\frac{q_0 \cdot (p_0 - O)}{2} = \frac{ \frac{9000}{119} \cdot \left( \frac{8964}{119} - 36 \right)}{2} = \frac{21060000}{14161} \approx 1487.18$

Ejemplo 2

Considerando la ecuación de demanda 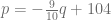$p = -\frac{9}{10}q +104$ y la ecuación de oferta $p = \frac{27}{100}q +46$ , calcule el punto de equilibrio del mercado; posteriormente calcule el excedente de los consumidores y el excedente de los fabricantes.

Para calcular el punto de equilibrio del mercado debemos igualar las expresiones que definen ambas rectas y luego despejamos la variable 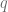$q$ .

$-\frac{9}{10}q +104 = \frac{27}{100}q+46$

$\Rightarrow \ -\frac{9}{10}q -\frac{27}{100}q = 46-104$

$\Rightarrow \ -\frac{117}{100}q = -58$

$\Rightarrow \ q = \frac{5800}{117}$

Una vez calculado el valor de 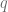$q$ , lo sustituimos en la recta de nuestra preferencia y calculamos el valor de 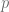$p$ . Sustituyamos entonces el valor 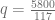$q=\frac{5800}{117}$ en la ecuación de demanda.

$p = \ -\frac{9}{10} \cdot \left( \frac{5800}{117} \right) + 104$

$= \ -\frac{580}{13} + 104$

$= \ \frac{772}{13}$

Por lo tanto, el punto de equilibrio del mercado $\left( \frac{5800}{117} , \frac{772}{13} \right)$ . Grafiquemos ahora el punto de equilibrio del mercado e identifiquemos las áreas que definen los excedentes.

Calculamos el Excedente de los Consumidores:

$\frac{q_0 \cdot (D - p_0)}{2} = \frac{ \frac{5800}{117} \cdot \left( 104 - \frac{772}{13} \right)}{2} = \frac{1682000}{1521} \approx 1105.85$

Calculamos el Excedente de los Fabricantes:

$\frac{q_0 \cdot (p_0 - O)}{2} = \frac{ \frac{5800}{117} \cdot \left( \frac{772}{13} - 46 \right)}{2} = \frac{168200}{507} \approx 331.76$

Anuncios

Ejemplo 3

Considerando la ecuación de demanda $p = -\frac{12}{25}q +171$ y la ecuación de oferta $p = \frac{3}{50}q +36$ , calcule el punto de equilibrio del mercado; posteriormente calcule el excedente de los consumidores y el excedente de los fabricantes.

Para calcular el punto de equilibrio del mercado debemos igualar las expresiones que definen ambas rectas y luego despejamos la variable 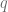$q$ .

$-\frac{12}{25}q +171 = \frac{3}{50}q+36$

$\Rightarrow \ -\frac{12}{25}q -\frac{3}{50}q = 36-171$

$\Rightarrow \ -\frac{27}{50}q = -135$

$\Rightarrow \ q = 250$

Una vez calculado el valor de 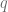$q$ , lo sustituimos en la recta de nuestra preferencia y calculamos el valor de 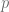$p$ . Sustituyamos entonces el valor $q=250$ en la ecuación de demanda.

$p = \ -\frac{12}{25} \cdot \left( 250 \right) + 171$

$= \ -120 + 171$

$= \ 51$

Por lo tanto, el punto de equilibrio del mercado $\left( 250 , 51 \right)$ . Grafiquemos ahora el punto de equilibrio del mercado e identifiquemos las áreas que definen los excedentes.

Calculamos el Excedente de los Consumidores:

$\frac{q_0 \cdot (D - p_0)}{2} = \frac{ 250 \cdot \left( 171 - 51 \right)}{2} = 15000$

Calculamos el Excedente de los Fabricantes:

$\frac{q_0 \cdot (p_0 - O)}{2} = \frac{ 250 \cdot \left( 51 - 36 \right)}{2} = 1875$

Ejemplo 4

Considerando la ecuación de demanda $p = -\frac{1}{10}q +115$ y la ecuación de oferta $p = \frac{87}{100}q +11$ , calcule el punto de equilibrio del mercado; posteriormente calcule el excedente de los consumidores y el excedente de los fabricantes.

Para calcular el punto de equilibrio del mercado debemos igualar las expresiones que definen ambas rectas y luego despejamos la variable 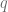$q$ .

$-\frac{1}{10}q +115 = \frac{87}{100}q+11$

$\Rightarrow \ -\frac{1}{10}q -\frac{87}{100}q = 11-115$

$\Rightarrow \ -\frac{97}{100}q = -104$

$\Rightarrow \ q = \frac{10400}{97}$

Una vez calculado el valor de 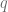$q$ , lo sustituimos en la recta de nuestra preferencia y calculamos el valor de 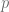$p$ . Sustituyamos entonces el valor 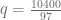$q=\frac{10400}{97}$ en la ecuación de demanda.

$p = \ -\frac{1}{10} \cdot \left( \frac{10400}{97} \right) + 115$

$= \ -\frac{1040}{97} + 115$

$= \ \frac{10115}{97}$

Por lo tanto, el punto de equilibrio del mercado 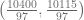$\left( \frac{10400}{97} , \frac{10115}{97} \right)$ . Grafiquemos ahora el punto de equilibrio del mercado e identifiquemos las áreas que definen los excedentes.

Calculamos el Excedente de los Consumidores:

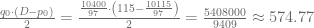
$\frac{q_0 \cdot (D - p_0)}{2} = \frac{ \frac{10400}{97} \cdot \left( 115 - \frac{10115}{97} \right)}{2} = \frac{5408000}{9409} \approx 574.77$

Calculamos el Excedente de los Fabricantes:

$\frac{q_0 \cdot (p_0 - O)}{2} = \frac{ \frac{10400}{97} \cdot \left( \frac{10115}{97} - 11 \right)}{2} = \frac{47049600}{9409} \approx 5000.49$

La Ecuación de Oferta

28.10.202025.08.2023 Anthonny Arias-García2 comentarios

La Curva de Oferta
1. Ejemplos
  1. Ejemplo 1
  2. Ejemplo 2

Suponga que usted es un productor de tomates y provee a un supermercado semanalmente, y ve que un kilo de tomates tiene un precio de $200$ Ps, considerando los costos de producción, le parece que este precio es generoso para usted por lo que decide proveer al supermercado con $40$ kilos de tomate. La semana siguiente vuelve al supermercado y ve que un kilo de tomates tiene un precio de $100$ Ps, considerando que está en la mitad del precio de la semana anterior, usted decide proveer al supermercado con $30$ kilos de tomate.

Nota: Perolitos (Ps.) es la moneda oficial de totumat.

También pudiera interesarte

Esta situación se presenta de forma general, pues al considerar el precio de un artículo, los productores proveerán más unidades del artículo cuando el precio es alto y proveerán menos unidades del artículo cuando el precio es bajo, esto se conoce como la oferta de un artículo.

Entonces, si bien podemos intuir que la oferta de un artículo aumenta a medida que el precio del artículo aumenta, nuestro propósito será el de determinar la forma cuantificable de esta relación.

La Curva de Oferta

Para esto, definimos un plano cartesiano cuyos ejes están definidos por la variable precio, denotada por $p$ y la variable cantidad, denotada por $q$ ; para mantener la simplicidad de los modelos, consideraremos una economía simple, es decir, tal que las variables $p$ y $q$ sólo pueden tener valores positivos. De esta forma, nos ubicaremos sólo en el primer cuadrante del plano cartesiano.

Veamos en los siguientes ejemplos, cómo conociendo la oferta y el precio de un artículo en un momento dado, podemos definir rectas que describen de forma general la oferta del artículo.

Anuncios