También pudiera interesarte
La Matriz Cuadrada
Dentro del conjunto de todas las matrices, encontraremos matrices con propiedades importantes. A continuación nos enfocaremos en un tipo de matrices con una cantidad de filas y columnas muy particular. Diremos que una matriz es una matriz cuadrada si esta tiene tiene la misma cantidad de filas que de columnas. Formalmente, diremos que una matriz es cuadrada si tiene
filas y
columnas, en este caso diremos que es de tamaño
. Escrito de forma exhaustiva, tenemos que

Las matrices cuadradas pueden tener distintos tamaños, veamos algunos ejemplos de matrices cuadradas para entender como se expresan.
Ejemplos
Ejemplo 1
La siguiente es una matriz cuadrada de tamaño , por lo tanto La siguiente es una matriz cuadrada de tamaño dos.

Ejemplo 2
La siguiente es una matriz cuadrada de tamaño , por lo tanto La siguiente es una matriz cuadrada de tamaño tres.

Ejemplo 3
La siguiente es una matriz cuadrada de tamaño , por lo tanto La siguiente es una matriz cuadrada de tamaño cuatro.

Ejemplo 5
La siguiente es una matriz cuadrada de tamaño , por lo tanto La siguiente es una matriz cuadrada de tamaño cinco.


























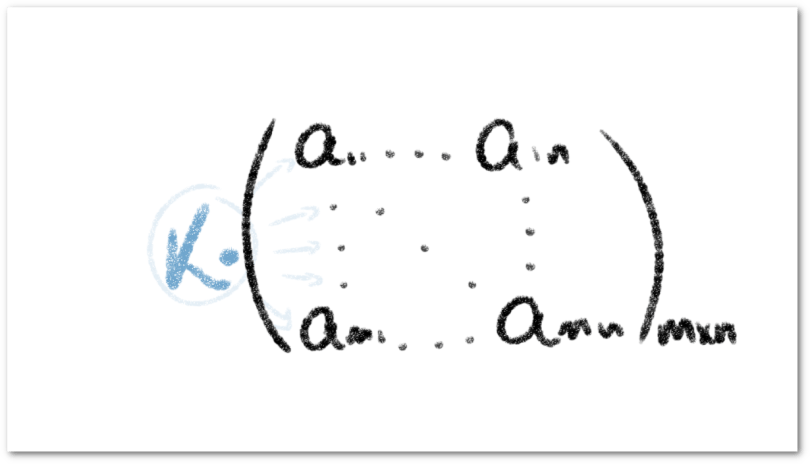













Debe estar conectado para enviar un comentario.