La cantidad de unidades fabricadas de un producto depende de muchos factores de producción. Entre estos se encuentran la mano de obra, el capital, el terreno, la maquinaria, etcétera. Por simplicidad, se supondrá que la producción sólo depende del trabajo y del capital.
También pudiera interesarte
Si la función proporciona la producción
cuando el productor emplea
unidades de trabajo (que usualmente la expresaremos como horas de trabajo semanal) y
unidades de capital, entonces esta función de producción, que depende de dos variables, se llama Función de Producción Conjunta.
Una vez fijadas las unidades de capital invertidas, podemos calcular la variación de la producción respecto a la cantidad horas de trabajo, es decir, la función de producción marginal respecto a la variable
Por ejemplo, si , entonces al aumentar en una hora la cantidad de horas de trabajo
cuando se fija el capital invertido en
, la producción aumentará en 10 unidades.
Por otra parte, una vez fijada la cantidad de horas a trabajar en una semana, podemos calcular la variación de la producción respecto al capital, es decir, la función de producción marginal respecto a la variable
Por ejemplo, si , entonces al aumentar en una unidad el capital
cuando se fija la cantidad de horas trabajadas en
, la producción aumentará en 50 unidades.
Ejemplo
Considerando una fábrica de plátano chips, ésta ha determinado que la función de producción es , donde
es el número de horas de trabajo por semana y
es el capital (expresado en miles de perolitos por semana) requerido para la producción semanal de
gruesas de plátano chips (Una gruesa es una cantidad de artículos equivalente a doce docenas, es decir, 144 artículos). Determine las funciones de producción marginal respecto a
y respecto a
; evalúelas en
e interprete los resultados.
Para esto, debemos notar que , por lo tanto
Luego,
Así, si mantenemos el capital en 16 mil Ps. y aumentamos la cantidad de horas de trabajo de 400 a 401 horas semanales, la producción aumentará en gruesas, es decir, en 14,4 empaques de plátano chips.
Por otra parte,
Luego,
Así, si fijamos la cantidad de horas de trabajo semanales en 400 y aumentamos el capital de 16 mil a 17 mil Ps., la producción aumentará en gruesas, es decir, en 360 empaques de plátano chips.
Funciones de Producción Cobb-Douglas
Un grupo importante de funciones de producción, son las Funciones de Producción Cobb-Douglas que se expresan como
La suma da información sobre los rendimientos a escala, es decir, la respuesta de la producción a un cambio proporcional en los insumos.
- Si esta suma es 1, existen rendimientos constantes a escala, es decir, la duplicación de los insumos duplica la producción, la triplicación de los insumos la triplica, y así sucesivamente.
- Si la suma es menor que 1, existen rendimientos decrecientes a escala: al duplicar los insumos, la producción crece en menos del doble.
- Si la suma es mayor que 1, hay rendimientos crecientes a escala; la duplicación de los insumos aumenta la producción en más del doble.
Particularmente nos interesará el caso . La importancia de este radica en que la función se expresar en función sus incrementos de la siguiente forma:
Si consideramos la función de producción de nuestro ejemplo, tendremos que sus derivadas parciales son y
, por lo tanto
Notamos que esta última expresión es precisamente nuestra función de producción.
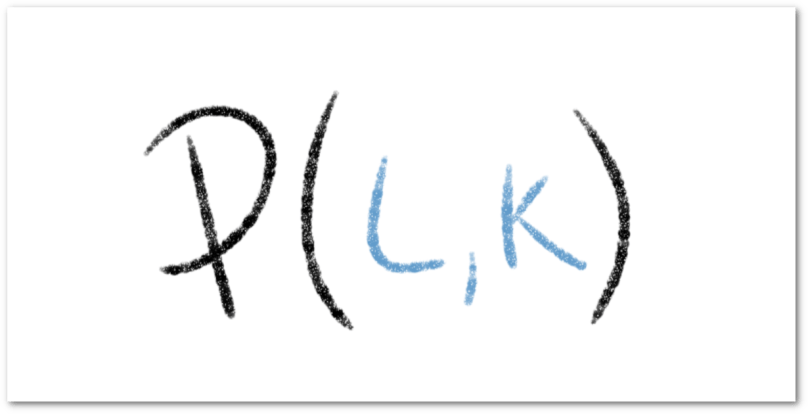






Debe estar conectado para enviar un comentario.