Uno de los mayores atractivos en el estudio de las sucesiones es su aplicabilidad en distintos ámbitos de la ciencia, ingeniería, economía y ámbitos sociales. Por lo que resulta necesario estudiar de forma detallada el comportamiento de algunas sucesiones en particular. En este caso veremos que hay sucesiones que se generan sumando el mismo número de forma iterada.
También pudiera interesarte
Definición de Sucesión Aritmética
Las sucesiones aritméticas (o progresiones aritméticas) son un tipo especial de sucesiones que parten desde un elemento básico y a partir de ahí, se suma una razón repetidas veces. Formalmente, diremos que es una sucesión aritmética si
Diremos que el primer elemento de la sucesión, es la base de la sucesión y, diremos que el número real
es la razón de la sucesión, podemos notar que este último está determinado por la diferencia entre dos elementos consecutivos de la sucesión.
Consideremos en los siguientes ejemplos, algunas sucesiones aritméticas para tener una idea más concreta de su comportamiento.
Ejemplos
Ejemplo 1
Si consideramos la sucesión . Su base será
y su razón será
. Por lo tanto, la forma general de esta sucesión está definida de la siguiente manera:
Ejemplo 2
Si consideramos la sucesión . Su base será
y su razón será
. Por lo tanto, la forma general de esta sucesión está definida de la siguiente manera:
Ejemplo 3
Si consideramos la sucesión . Su base será
y su razón será
. Por lo tanto, la forma general de esta sucesión está definida de la siguiente manera:
Ejemplo 4
Si consideramos la sucesión . Su base será
y su razón será
. Por lo tanto, la forma general de esta sucesión está definida de la siguiente manera:
Ejemplo 5
Si consideramos la sucesión . Su base será
y su razón será
. Por lo tanto, la forma general de esta sucesión está definida de la siguiente manera:
Considerando la razón de una sucesión aritmética podemos determinar el comportamiento de la misma. Veamos entonces lo que podemos concluir:
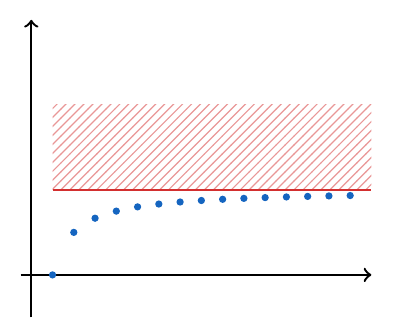
- Si la razón de la sucesión es positiva, es decir,
, entonces la sucesión es creciente y al ser creciente, el primer elemento será su mínimo (e ínfimo), además será divergente hacia más infinito.
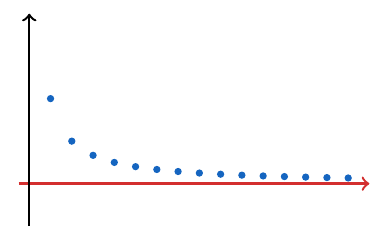
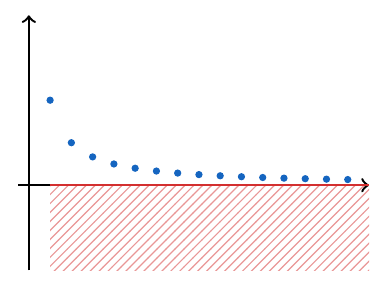
- Si la razón de la sucesión es negativa, es decir,
, entonces la sucesión es decreciente y al ser decreciente, el primer elemento será su máximo (y supremo), además será divergente hacia menos infinito.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Cómo determinar la fórmula general de una Sucesión Aritmética
Si bien hemos visto que a partir de dos elementos consecutivos de una sucesión aritmética podemos determinar la razón de la sucesión y a partir de esta podemos determinar la base de la sucesión, es posible determinar la fórmula general de una sucesión aritmética considerando dos elementos cualesquiera de esta.
Formalmente, si consideramos dos elementos de una sucesión aritmética y
, podemos determinar el valor de
y de
calculando la solución del siguiente sistema de ecuaciones lineales:
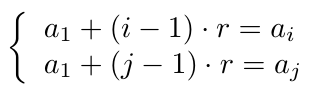
Veamos en los siguientes ejemplos como determinar la fórmula general de una sucesión aritmética usando esta técnica.
Ejemplos
Ejemplo 6
Considerando y
dos elementos de una sucesión aritmética. Determine la fórmula general de esta sucesión.
Para esto, calculamos la solución del siguiente sistema de ecuaciones lineales:

Para calcular la solución de este sistema de ecuaciones restamos ambas ecuaciones, notando que para obtener la siguiente ecuación
A partir de esta ecuación podemos despejar , para obtener que
y sustituirlo en la ecuación de nuestra preferencia para calcular
.
Sustituimos en la primera ecuación y despejamos
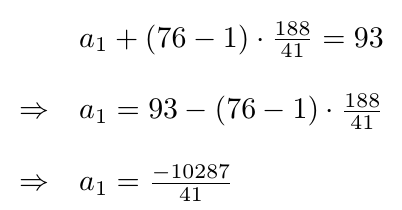
Finalmente, y de
, podemos expresar la fórmula general que define a la sucesión de la siguiente manera:
Ejemplo 7
Considerando y
dos elementos de una sucesión aritmética. Determine la fórmula general de esta sucesión.
Para esto, calculamos la solución del siguiente sistema de ecuaciones lineales:
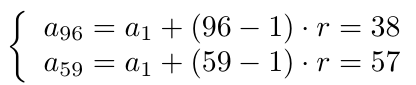
Para calcular la solución de este sistema de ecuaciones restamos ambas ecuaciones, notando que para obtener la siguiente ecuación
A partir de esta ecuación podemos despejar , para obtener que
y sustituirlo en la ecuación de nuestra preferencia para calcular
.
Sustituimos en la primera ecuación y despejamos

Finalmente, y de
, podemos expresar la fórmula general que define a la sucesión de la siguiente manera:
Ejemplo 8
Considerando y
dos elementos de una sucesión aritmética. Determine la fórmula general de esta sucesión.
Para esto, calculamos la solución del siguiente sistema de ecuaciones lineales:
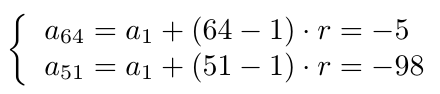
Para calcular la solución de este sistema de ecuaciones restamos ambas ecuaciones, notando que para obtener la siguiente ecuación
A partir de esta ecuación podemos despejar , para obtener que
y sustituirlo en la ecuación de nuestra preferencia para calcular
.
Sustituimos en la primera ecuación y despejamos

Finalmente, y de
, podemos expresar la fórmula general que define a la sucesión de la siguiente manera:
Ejemplo 9
Considerando y
dos elementos de una sucesión aritmética. Determine la fórmula general de esta sucesión.
Para esto, calculamos la solución del siguiente sistema de ecuaciones lineales:
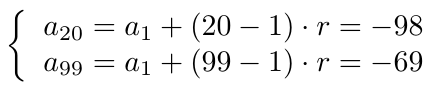
Para calcular la solución de este sistema de ecuaciones restamos ambas ecuaciones, notando que para obtener la siguiente ecuación
A partir de esta ecuación podemos despejar , para obtener que
y sustituirlo en la ecuación de nuestra preferencia para calcular
.
Sustituimos en la primera ecuación y despejamos

Finalmente, y de
, podemos expresar la fórmula general que define a la sucesión de la siguiente manera:


























Debe estar conectado para enviar un comentario.