- Diferencia de una función
- Diferencial de una función
- Relación entre diferenciales y diferencias
- Cálculo del diferencial de una función
- Ejemplos
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
- Ejemplo 4
Las diferencias y las razones de cambio son elementos fundamentales para el estudio de funciones diferenciables pues, al sentar estos la base para calcular la derivada de una función, podemos establecer relaciones que permiten aproximar valores de la función a través de su derivada.
También pudiera interesarte
Diferencia de una función
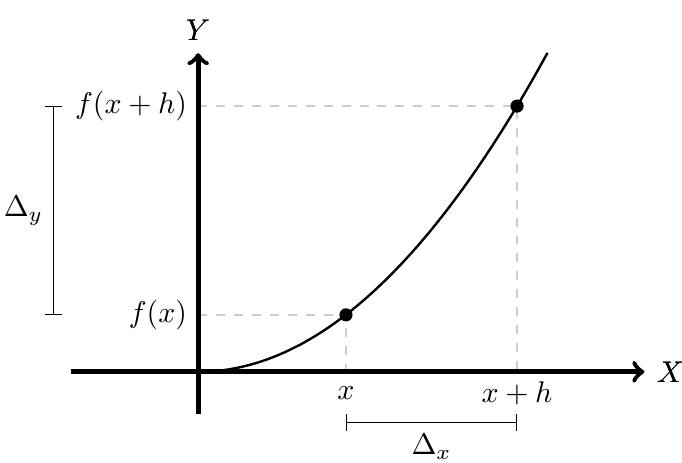
Al estudiar el comportamiento de una función  diferenciable en todo su dominio, si consideramos un valor
diferenciable en todo su dominio, si consideramos un valor  en el dominio de ella, y
en el dominio de ella, y  un valor incrementado de
un valor incrementado de  , definimos la diferencia entre estos dos valores (la diferencia en x) de la siguiente manera:
, definimos la diferencia entre estos dos valores (la diferencia en x) de la siguiente manera:
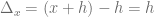
De igual forma, al considerar las imágenes de estos dos valores a través de la función, es decir, de  y
y  ; definimos la diferencia entre estas dos imágenes (la diferencia en y) de la siguiente manera:
; definimos la diferencia entre estas dos imágenes (la diferencia en y) de la siguiente manera:

Es decir, la diferencia en  mide cuanto varía la función cuando la variable
mide cuanto varía la función cuando la variable  varía con medida igual a la diferencia en
varía con medida igual a la diferencia en  .
.
Nota: hemos usado la letra griega delta mayúscula « » pues es la letra equivalente a la letra «d» en el español.
» pues es la letra equivalente a la letra «d» en el español.
Estas diferencias se aprecian con mayor claridad al observar la gráfica de la función  :
:
El estudio de estas diferencias es de vital importancia para el cálculo de derivadas, pues al considerar valores muy pequeños de la diferencia 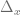 , el siguiente cociente se aproximará a la derivada de la función
, el siguiente cociente se aproximará a la derivada de la función  :
:
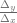
Debemos recordar que la derivada de la función  está definida de la siguiente forma:
está definida de la siguiente forma:

Diferencial de una función
Por otra parte, al estudiar el comportamiento de la recta tangente a la función  en el punto
en el punto  , llamémosla
, llamémosla 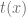 . Si consideramos un valor
. Si consideramos un valor  , y
, y  un valor incrementado de
un valor incrementado de  , definimos el diferencial entre estos dos valores (el diferencial de x) de la siguiente manera:
, definimos el diferencial entre estos dos valores (el diferencial de x) de la siguiente manera:

De igual forma, al considerar las imágenes de estos dos valores a través de la recta tangente, es decir, de 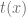 y
y  ; definimos el diferencial entre estas dos imágenes (el diferencial de y) de la siguiente manera:
; definimos el diferencial entre estas dos imágenes (el diferencial de y) de la siguiente manera:

Estos diferenciales se aprecian con mayor claridad al observar la gráfica de la función  :
:
El estudio de estos diferenciales es de vital importancia para el cálculo de derivadas, el siguiente cociente, al ser exactamente la pendiente de la recta tangente a la curva en el punto  , es la derivada de la función
, es la derivada de la función  :
:

De esta igualdad, podemos despejar 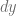 y así, podemos plantear la siguiente igualdad, que nos define la forma en que se calcula el diferencial de la función
y así, podemos plantear la siguiente igualdad, que nos define la forma en que se calcula el diferencial de la función  :
:
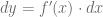
Es decir, el diferencial de  mide cuanto incrementa la pendiente recta tangente cuando la variable
mide cuanto incrementa la pendiente recta tangente cuando la variable  presenta un incremento con medida igual al diferencial de
presenta un incremento con medida igual al diferencial de  .
.
Relación entre diferenciales y diferencias
Hemos visto que las diferencias y los diferenciales están relacionados íntimamente con la derivada de una función, entonces, notando que la diferencia en  y el diferencial de
y el diferencial de  son exactamente el mismo elemento, es decir,
son exactamente el mismo elemento, es decir,  ; debemos estudiar, con particular interés, la relación entre
; debemos estudiar, con particular interés, la relación entre  y
y 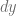 .
.
Hemos dicho que el cociente 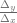 se aproxima a la derivada de la función, por lo tanto, podemos considerar un número real
se aproxima a la derivada de la función, por lo tanto, podemos considerar un número real 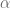 que depende de
que depende de 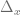 que nos permite establecer la siguiente relación:
que nos permite establecer la siguiente relación:

Entonces, al multiplicar en ambos lados de la ecuación por 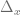 , despejamos
, despejamos  obteniendo que
obteniendo que

De esta forma, si nos fijamos que el primer sumando es determinado por  , que es justamente
, que es justamente 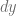 , nos damos cuenta que
, nos damos cuenta que 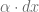 que representa el excedente sobre
que representa el excedente sobre 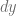 . Estos dos sumandos se aprecian con mayor claridad al observar la gráfica de la función
. Estos dos sumandos se aprecian con mayor claridad al observar la gráfica de la función  .
.
Considerando entonces que  , a medida que se hace pequeño el diferencial
, a medida que se hace pequeño el diferencial  también lo hará
también lo hará 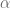 , y en consecuencia, se hará aún más pequeño el producto
, y en consecuencia, se hará aún más pequeño el producto 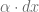 . Por lo tanto,
. Por lo tanto,
Si 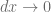 , entonces
, entonces 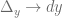
Concluimos entonces, que el diferencial de  es una aproximación lineal (a través de la recta tangente a la curva) de la diferencia de
es una aproximación lineal (a través de la recta tangente a la curva) de la diferencia de  , es decir,
, es decir,

Cálculo del diferencial de una función
Si consideramos una función  , el diferencial de esta puede expresarse de las siguientes formas:
, el diferencial de esta puede expresarse de las siguientes formas:
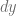 ó
ó 
En los siguientes ejemplos, veremos como calcular el diferencial de una función.
Ejemplos
Ejemplo 1
Considerando la función  , para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:
, para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:

Ejemplo 2
Considerando la función  , para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:
, para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:

Ejemplo 3
Considerando la función  , para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:
, para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:

Ejemplo 4
Considerando la función  , para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:
, para calcular su diferencial, basta con calcular la derivada de la función y multiplicarla por el diferencial de x, de la siguiente forma:




























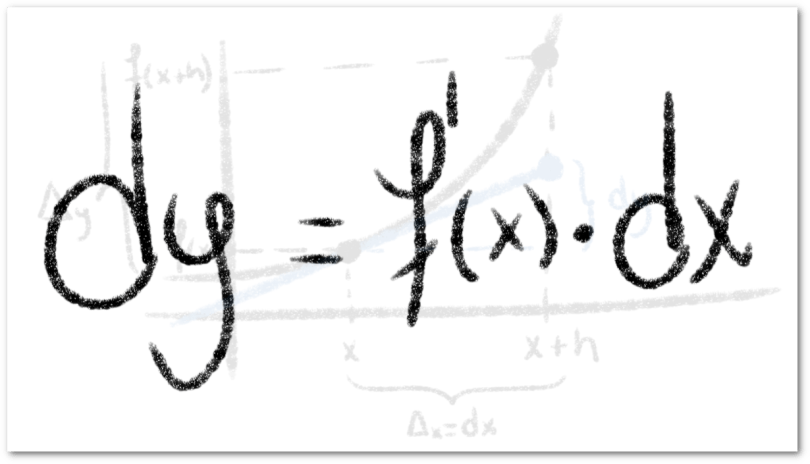


Debe estar conectado para enviar un comentario.