Autor: Anthonny Arias-García

Sub-Coordinador de Matemáticas de la Facultad de Ciencias Económicas y Sociales, Universidad de Los Andes, Mérida, Venezuela.
Ejercicios Propuestos

Ejercicios Propuestos – Ecuaciones Polinómicas

Anthonny Arias-García1 comentario
Anuncios

Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.

Calcule la solución de la ecuación polinómica planteada (igualando toda la expresión a cero, agrupando todos los elementos en el lado izquierdo de la igualdad) y posteriormente factorice la expresión polinómica resultante.

  1. x^{2} + x - 68 = x - 4
  2. x^{2} + 18 x + 73 = x + 1
  3. x^{2} + 5 x + 6 = x + 6
  4. x^{2} - 5 x + 2 = x - 3

  1. - 6 x^{2} - 26 x + 56 = 4 x^{2} + 4 x - 224
  2. - 14 x^{2} - 26 x + 568 = - 10 x^{2} - 30 x + 400
  3. 5 x^{2} + 32 x + 48 = 2 x^{2} + 26 x + 72
  4. - 2 x - 8 = - x^{2} - 9 x - 20

  1. 3 x^{3} - 137 x^{2} + 64 x + 4330 = - 7 x^{3} - 7 x^{2} + 154 x + 280
  2. 2 x^{3} + 8 x^{2} - 156 x - 336 = - x^{3} - x^{2} + 6 x
  3. - 18 x^{3} + 36 x^{2} - 54 x + 1944 = - 9 x^{3} + 144 x^{2} - 297 x - 2430
  4. - 17 x^{3} - 162 x^{2} + 357 x + 4750 = - 8 x^{3} - 72 x^{2} + 528 x + 4480

  1. - 9 x^{4} + 18 x^{3} + 417 x^{2} - 126 x - 3840 = - 3 x^{4} + 81 x^{2} + 162 x
  2. 9 x^{4} + 123 x^{3} + 369 x^{2} - 249 x + 756 = 3 x^{4} + 33 x^{3} - 39 x^{2} - 753 x + 756
  3. 6 x^{4} - 12 x^{3} - 656 x^{2} - 1418 x + 31780 = x^{4} - 22 x^{3} + 159 x^{2} - 418 x + 280
  4. x^{4} + 44 x^{3} + 530 x^{2} + 1972 x + 4365 = - 8 x^{4} - 64 x^{3} + 584 x^{2} + 4960 x + 7200

Anuncios
Ejercicios Propuestos

Ejercicios Propuestos – Productos Complementarios y Suplementarios

Anthonny Arias-García2 comentarios
Anuncios

Para cada una de las siguientes funciones de demanda para los productos A y B. Calcule \dfrac{\partial q_A}{\partial p_A}, \dfrac{\partial q_A}{\partial p_B}, \dfrac{\partial q_B}{\partial p_B} y \dfrac{\partial q_B}{\partial p_A}; Determine si estas ecuaciones son de demanda y en caso de serlo, determine si los productos A y B son complementarios, suplementarios o ninguna de las dos. Recordando que

Dos productos A y B son Suplementarios si

\dfrac{\partial q_A}{\partial p_B} > 0 \text{ y } \dfrac{\partial q_B}{\partial p_A} > 0

Dos productos A y B son Complementarios si

\dfrac{\partial q_A}{\partial p_B} < 0 \text{ y } \dfrac{\partial q_B}{\partial p_A} < 0

  1. q_A = 200 - 30p_A + 5p_B
    q_B = 320 + 12p_A - 60 p_B
  2. q_A = 1000 - 68p_A + 15p_B
    q_B = 250 + 9p_A - 50 p_B
  3. q_A = 5 - 20p_A + 30p_B
    q_B = 10 + 31p_A - 31 p_B
  4. q_A = 10 - 0.2p_A + 0.3p_B
    q_B = 12 + 0.4p_A - 0.95p_B

  1. q_A = 3.5 - 5p_A - 6p_B
    q_B = 4.2 - 7p_A - 7 p_B
  2. q_A = 4.2 - 7.8p_A - 9p_B
    q_B = 13 - 3.7p_A - 2.6 p_B
  3. q_A = 7 - 5.4p_A - 9.6p_B
    q_B = 10 - 2.3 p_A - 4 p_B
  4. q_A = 1.9 - 8.1p_A - 4p_B
    q_B = 2.8 - 5.3p_A - 5.5 p_B

  1. q_A = 10\sqrt[3]{p_B} \cdot \sqrt[3]{p_A^2}
    q_B = 9.2\sqrt[3]{p_A} \cdot \sqrt[3]{p_B^2}
  2. q_A = 7\sqrt[4]{p_B} \cdot \sqrt[5]{p_A^4}
    q_B = 8\sqrt{p_A^3} \cdot \sqrt[4]{p_B^3}
  3. q_A = 5.5\sqrt{p_B^5} \cdot \sqrt[5]{p_A^3}
    q_B = 6.8\sqrt[7]{p_A^8} \cdot \sqrt[9]{p_B^7}
  4. q_A = 4\sqrt[3]{p_B^6} \cdot \sqrt[10]{p_A^2}
    q_B = 7.3\sqrt[5]{p_A^2} \cdot \sqrt[4]{p_B^6}
  1. q_A = 10\frac{\sqrt[3]{p_A} }{ \sqrt[3]{p_B^2}}
    q_B = 9.2\frac{\sqrt[3]{p_A} }{ \sqrt[3]{p_B^2}}
  2. q_A = 7\frac{\sqrt[4]{p_A} }{ \sqrt[5]{p_B^4}}
    q_B = 8\frac{\sqrt{p_B^3} }{ \sqrt[4]{p_A^3}}
  3. q_A = 5.5\frac{\sqrt{p_B^5} }{ \sqrt[5]{p_A^3}}
    q_B = 6.8\frac{\sqrt[7]{p_A^8} }{ \sqrt[9]{p_B^7}}
  4. q_A = 4\frac{\sqrt[3]{p_B^6} }{ \sqrt[10]{p_A^2}}
    q_B = 7.3\frac{\sqrt[5]{p_B^2} }{ \sqrt[4]{p_A^6}}

  1. q_A = \frac{11}{ \sqrt[3]{p_B} \cdot \sqrt[3]{p_A^2}}
    q_B = \frac{8.2}{ \sqrt[3]{p_A} \cdot \sqrt[3]{p_B^2}}
  2. q_A = \frac{8}{ \sqrt[4]{p_B} \cdot \sqrt[5]{p_A^4}}
    q_B = \frac{7}{ \sqrt{p_A^3} \cdot \sqrt[4]{p_B^3}}
  3. q_A = \frac{6.5}{ \sqrt{p_B^5} \cdot \sqrt[5]{p_A^3}}
    q_B = \frac{5.8}{ \sqrt[7]{p_A^8} \cdot \sqrt[9]{p_B^7}}
  4. q_A = \frac{5}{ \sqrt[3]{p_B^6} \cdot \sqrt[10]{p_A^2}}
    q_B = \frac{6.3}{ \sqrt[5]{p_A^2} \cdot \sqrt[4]{p_B^6}}

  1. q_A = {\rm e}^{3p_A} \cdot {\rm e}^{6p_B}
    q_B = {\rm e}^{5p_A} \cdot {\rm e}^{6p_B}
  2. q_A = {\rm e}^{10p_A} \cdot {\rm e}^{-7p_B}
    q_B = {\rm e}^{-5p_A} \cdot {\rm e}^{6p_B}
  3. q_A = {\rm e}^{-4p_A} \cdot {\rm e}^{3p_B}
    q_B = {\rm e}^{9p_A} \cdot {\rm e}^{-6p_B}
  4. q_A = {\rm e}^{-7p_A} \cdot {\rm e}^{-8p_B}
    q_B = {\rm e}^{-12p_A} \cdot {\rm e}^{-p_B}

Anuncios

Solución

Ejercicio 20

Ejercicio 23

Ejercicios Propuestos

Ejercicios Propuestos – Tasa Técnica de Sustitución y Tasa Marginal de Sustitución

Anthonny Arias-García2 comentarios
Anuncios

Tasa Técnica de Sustitución (TTS)

1.- Una compañía que fabrica celulares ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{45}{59} \cdot \sqrt[ 86 ]{ l^{81} } \cdot \sqrt[ 86 ]{ k^{5} }

Determine la Tasa Técnica de Sustitución.

2.- Una compañía que fabrica neveras ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{37}{56} \cdot \sqrt[ 97 ]{ l^{95} } \cdot \sqrt[ 97 ]{ k^{2} }

Determine la Tasa Técnica de Sustitución.

3.- Una compañía que fabrica cristales ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{61}{99} \cdot \sqrt[ 19 ]{ l^{18} } \cdot \sqrt[ 19 ]{ k }

Determine la Tasa Técnica de Sustitución.

4.- Una compañía que fabrica trajes de baño ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{14}{27} \cdot \sqrt[ 6 ]{ l^{5} } \cdot \sqrt[ 6 ]{ k }

Determine la Tasa Técnica de Sustitución.

5.- Una compañía que fabrica metras/canicas ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{119}{22} \cdot \sqrt[ 44 ]{ l^{5} } \cdot \sqrt[ 44 ]{ k^{39} }-\sqrt[ 44 ]{ l^{49} } \cdot \sqrt[ 44 ]{ k^{83} }

Determine la Tasa Técnica de Sustitución.

6.- Una compañía que fabrica helados ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{315}{59} \cdot \sqrt[ 77 ]{ l^{52} } \cdot \sqrt[ 77 ]{ k^{25} }-\sqrt[ 77 ]{ l^{129} } \cdot \sqrt[ 77 ]{ k^{102} }

Determine la Tasa Técnica de Sustitución.

7.- Una compañía que fabrica jabones de baño ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{219}{33} \cdot \sqrt[ 15 ]{ l } \cdot \sqrt[ 15 ]{ k^{14} }-\sqrt[ 15 ]{ l^{16} } \cdot \sqrt[ 15 ]{ k^{29} }

Determine la Tasa Técnica de Sustitución.

8.- Una compañía que fabrica jugos empaquetados ha determinado que cuando se emplean l horas de mano de obra y se invierten k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{158}{95} \cdot \sqrt[ 32 ]{ l^{3} } \cdot \sqrt[ 32 ]{ k^{29} }-\sqrt[ 32 ]{ l^{35} } \cdot \sqrt[ 32 ]{ k^{61} }

Determine la Tasa Técnica de Sustitución.

Anuncios

Tasa Marginal de Sustitución

Reduzcamos una situación en la que un individuo de la sociedad sólo puede dedicar su tiempo a dos usos respecto al mercado: horas de trabajo y horas de no trabajo.

Denotaremos las horas de trabajo con la variable l (labor en inglés) y si por cada hora de trabajo obtiene un ingreso de w, entonces, considerando que este individuo puede adquirir bienes si trabaja, definimos la variable consumo c = l \cdot w.

Definiremos las horas de no trabajo como horas de ocio y las denotaremos con la variable h, estas representan las horas que dedica a trabajar en casa (no en el mercado), ver televisión o navegar en las redes sociales.

9.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{12}{83} \cdot \sqrt[ 55 ]{ c^{18} } \cdot \sqrt[ 55 ]{ h^{37} }

Determine la Tasa Marginal de Sustitución.

10.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{25}{38} \cdot \sqrt[ 55 ]{ c^{27} } \cdot \sqrt[ 55 ]{ h^{28} }

Determine la Tasa Marginal de Sustitución.

11.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{12}{31} \cdot \sqrt[ 97 ]{ c^{40} } \cdot \sqrt[ 97 ]{ h^{57} }

Determine la Tasa Marginal de Sustitución.

12.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{25}{74} \cdot \sqrt[ 31 ]{ c^{22} } \cdot \sqrt[ 31 ]{ h^{9} }

Determine la Tasa Marginal de Sustitución.

13.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{18}{89} \cdot \sqrt[ 43 ]{ c^{9} } \cdot \sqrt[ 43 ]{ h^{63} }

Determine la Tasa Marginal de Sustitución.

14.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{54}{77} \cdot \sqrt[ 83 ]{ c^{89} } \cdot \sqrt[ 83 ]{ h^{4} }

Determine la Tasa Marginal de Sustitución.

15.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{82}{85} \cdot \sqrt[ 33 ]{ c^{47} } \cdot \sqrt[ 48 ]{ h }

Determine la Tasa Marginal de Sustitución.

16.- Suponga que las preferencias de un individuo están determinadas a través de la siguiente función de utilidad:

U(c,h) = \frac{21}{88} \cdot \sqrt[ 9 ]{ c^{41} } \cdot \sqrt[ 91 ]{ h^{50} }

Determine la Tasa Marginal de Sustitución.

Anuncios

Solución

Ejercicio 1

Ejercicios Propuestos

Ejercicios Propuestos – Ecuaciones Lineales

Anthonny Arias-García1 comentario

Calcule la solución de las siguientes ecuaciones lineales usando en cada paso los Axiomas Algebraicos de los Números Reales, explique cada paso con sus propias palabras.

Ecuaciones Lineales

  1. x + 6 = 9
  2. x - 9 = 6
  3. x + 5 = -10
  4. x - 3 = -30

  1. 7x + 1 = 10
  2. 5x - 4 = 5
  3. 4x + 10 = -5
  4. 4x - 7 = -15

  1. 2 + x = 3
  2. 7 - 6x = 10
  3. -8 + 16x = -7
  4. 3 - 8x = -9
  1. 3 + x = 8x
  2. 2 - 8x = 9x
  3. -5 + 81x = -9x
  4. 2 - 18x = -4x

  1. 1 + x = 18 + 8x
  2. 2 - 8x = 2 + 2x
  3. 6 - 5x = 9 - 9x
  4. -3 + 9x = -6 - 6x

  1. 3 + 11x = 8 + 8x - 10x
  2. 12 - 81x = 21x + 2x
  3. 6x - 5x + 10 = 9 - 9x
  4. -3x + 9x + 20 = 12x -16 - 6x

Ecuaciones Lineales con Valor Absoluto

  1. |x + 6| = 9
  2. |x - 9| = 6
  3. |x + 5| = 0
  4. |x - 3| = -30

  1. |7x + 1| = 10
  2. |5x - 4| = 5
  3. |4x + 10| = 15
  4. |4x - 7| = 30

  1. |2 + x| = 3
  2. |7 - 6x| = 0
  3. |-8 + 16x| = 7
  4. |3 - 8x| = -9

Ejercicios Propuestos

Ejercicios Propuestos – Análisis Marginal: Costos Conjuntos y Producción

Anthonny Arias-García2 comentarios
Anuncios

Funciones de Costos Conjuntos

1.- Una compañía fabrica celulares en dos presentaciones: Pixel, cuya cantidad producida se presenta con x y Pixel XL, cuya cantidad producida se presenta con y. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

c(x,y) = 0.1 x^{3} + 2.3 x^{2} - 65.0 x + 0.2 y^{3} - 2.2 y^{2} - 51.4 y + 5953

Evalúe las funciones \dfrac{\partial c}{\partial x} y \dfrac{\partial c}{\partial y} en el punto P=( 63 , 35 ) e interprete los resultados.

2.- Una compañía fabrica neveras en dos presentaciones: con congelador, cuya cantidad producida se presenta con x y sin congelador, cuya cantidad producida se presenta con y. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

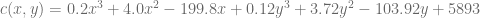
c(x,y) = 0.2 x^{3} + 4.0 x^{2} - 199.8 x + 0.12 y^{3} + 3.72 y^{2} - 103.92 y + 5893

Evalúe las funciones \dfrac{\partial c}{\partial x} y \dfrac{\partial c}{\partial y} en el punto P=( 75 , 95 ) e interprete los resultados.

3.- Una compañía fabrica cristales en dos presentaciones: con anti-reflejo, cuya cantidad producida se presenta con x y sin anti-reflejo, cuya cantidad producida se presenta con y. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

c(x,y) = 0.33 x^{3} - 1.6 x^{2} - 68.32 x + 0.2 y^{3} + 3.8 y^{2} - 150.0 y + 5296

Evalúe las funciones \dfrac{\partial c}{\partial x} y \dfrac{\partial c}{\partial y} en el punto P=( 32 , 22 ) e interprete los resultados.

4.- Una compañía fabrica trajes de baño en dos presentaciones: para damas, cuya cantidad producida se presenta con x y para caballeros, cuya cantidad producida se presenta con y. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

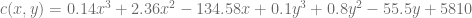
c(x,y) = 0.14 x^{3} + 2.36 x^{2} - 134.58 x + 0.1 y^{3} + 0.8 y^{2} - 55.5 y + 5810

Evalúe las funciones \dfrac{\partial c}{\partial x} y \dfrac{\partial c}{\partial y} en el punto P=( 39 , 43 ) e interprete los resultados.

5.- Una compañía fabrica metras/canicas en tres presentaciones: ojo de gato, cuya cantidad producida se presenta con x, coquito, cuya cantidad producida se presenta con y y bolondrones, cuya cantidad producida se presenta con z. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

c(x,y,z) = 0.5 x^{3} - 7.0 x^{2} - 96.0 x + 0.11 y^{3} + 0.47 y^{2} - 55.8 y + 0.33 z^{3} - 3.61 z^{2} - 16.84 z + 8878

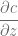Evalúe las funciones \dfrac{\partial c}{\partial x}, \dfrac{\partial c}{\partial y} y \dfrac{\partial c}{\partial z} en el punto P=( 92 , 59 , 98 ) e interprete los resultados.

6.- Una compañía fabrica helados en tres presentaciones: mantecado, cuya cantidad producida se presenta con x, chocolate, cuya cantidad producida se presenta con y y fresa, cuya cantidad producida se presenta con z. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

c(x,y,z) = 0.25 x^{3} + 1.25 x^{2} - 105.5 x + 0.1 y^{3} + 0.6 y^{2} - 24.7 y + 0.12 z^{3} - 0.88 z^{2} - 35.04 z + 8303

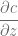Evalúe las funciones \dfrac{\partial c}{\partial x}, \dfrac{\partial c}{\partial y} y \dfrac{\partial c}{\partial z} en el punto P=( 83 , 94 , 92 ) e interprete los resultados.

7.- Una compañía fabrica jabones de baño en tres presentaciones: finas esencias, cuya cantidad producida se presenta con x, flor primaveral, cuya cantidad producida se presenta con y y perro mojado, cuya cantidad producida se presenta con z. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

c(x,y,z) = 0.1 x^{3} + 8.0 x^{2} - 192.5 x + 0.17 y^{3} + 5.6 y^{2} - 173.88 y + 0.33 z^{3} + 0.07 z^{2} - 124.56 z + 9163

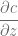Evalúe las funciones \dfrac{\partial c}{\partial x}, \dfrac{\partial c}{\partial y} y \dfrac{\partial c}{\partial z} en el punto P=( 80 , 46 , 24 ) e interprete los resultados.

8.- Una compañía fabrica jugos empaquetados en tres presentaciones: manzana, cuya cantidad producida se presenta con x, pera, cuya cantidad producida se presenta con y y durazno, cuya cantidad producida se presenta con z. Ésta ha determinado que la función de Costos Conjuntos está expresada de la siguiente forma:

c(x,y,z) = 0.14 x^{3} + 3.22 x^{2} - 169.4 x + 0.12 y^{3} + 2.48 y^{2} - 95.4 y + 0.2 z^{3} + 6.4 z^{2} - 173.6 z + 8464

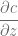Evalúe las funciones \dfrac{\partial c}{\partial x}, \dfrac{\partial c}{\partial y} y \dfrac{\partial c}{\partial z} en el punto P=( 105 , 85 , 83 ) e interprete los resultados.

Anuncios

Funciones de Producción

9.- Una compañía que fabrica celulares ha determinado que cuando se emplean 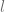l horas de mano de obra y se invierten 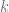k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{45}{59} \cdot \sqrt[ 86 ]{ l^{81} } \cdot \sqrt[ 86 ]{ k^{5} }

Evalúe las funciones \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 50 , 659 ) e interprete los resultados.

10.- Una compañía que fabrica neveras ha determinado que cuando se emplean 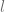l horas de mano de obra y se invierten 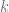k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{37}{56} \cdot \sqrt[ 97 ]{ l^{95} } \cdot \sqrt[ 97 ]{ k^{2} }

Evalúe las funciones \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 100 , 295 ) e interprete los resultados.

11.- Una compañía que fabrica cristales ha determinado que cuando se emplean 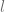l horas de mano de obra y se invierten 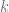k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{61}{99} \cdot \sqrt[ 19 ]{ l^{18} } \cdot \sqrt[ 19 ]{ k }

Evalúe las funciones que \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 80 , 909 ) e interprete los resultados.

12.- Una compañía que fabrica trajes de baño ha determinado que cuando se emplean 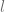l horas de mano de obra y se invierten 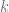k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{14}{27} \cdot \sqrt[ 6 ]{ l^{5} } \cdot \sqrt[ 6 ]{ k }

Evalúe las funciones \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 60 , 372 ) e interprete los resultados.

13.- Una compañía que fabrica metras/canicas ha determinado que cuando se emplean 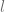l horas de mano de obra y se invierten 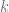k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{9}{13} \cdot \sqrt[ 97 ]{ l^{31} } \cdot \sqrt[ 97 ]{ k^{66} }

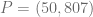Evalúe las funciones \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 50 , 807 ) e interprete los resultados.

14.- Una compañía que fabrica helados ha determinado que cuando se emplean 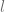l horas de mano de obra y se invierten 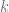k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{61}{86} \cdot \sqrt[ 24 ]{ l^{7} } \cdot \sqrt[ 24 ]{ k^{17} }

Evalúe las funciones \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 20 , 1091 ) e interprete los resultados.

15.- Una compañía que fabrica jabones de baño ha determinado que cuando se emplean 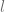l horas de mano de obra y se invierten 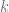k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{15}{68} \cdot \sqrt[ 90 ]{ l^{17} } \cdot \sqrt[ 90 ]{ k^{73} }

Evalúe las funciones \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 70 , 389 ) e interprete los resultados.

16.- Una compañía que fabrica jugos empaquetados ha determinado que cuando se emplean 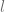l horas de mano de obra y se invierten 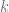k miles de bolívares, la función de producción está expresada de la siguiente forma:

P(l,k) = \frac{13}{24} \cdot \sqrt[ 82 ]{ l^{61} } \cdot \sqrt[ 82 ]{ k^{21} }

Evalúe las funciones \dfrac{\partial P}{\partial l} y \dfrac{\partial P}{\partial k} en el punto P=( 80 , 661 ) e interprete los resultados.

Anuncios