Una vez que hemos estudiado las ecuaciones de demanda y las ecuaciones de oferta, es claro que los productores prefieren vender a un precio alto y los consumidores prefieren comprar a un precio bajo, es por esto que se debe llegar a un consenso entre ambas partes de forma que ninguna de las dos se vea perjudicada.
Recordando que estas ecuaciones definen rectas, podemos, de forma matemática, establecer este consenso definiendo el punto de equilibrio del mercado como el punto de intersección entre ambas rectas. Gráficamente, está interpretado de la siguiente forma:

Calculando el punto de equilibrio, es posible fijar el precio de un artículo, de forma que los consumidores demandarán la misma cantidad de unidades que los productores están ofertando. Dicho precio será conocido como el precio de equilibrio y las cantidades serán conocidas como cantidades de equilibrio.
Veamos en los siguientes ejemplos, cómo calcular el punto de equilibrio en una economía simple una vez que ya contamos con las ecuaciones de demanda y oferta.
Ejemplos
Ejemplo 1
Considerando las ecuaciones y
que describen la demanda y la oferta de zanahorias en una pequeña tienda de verduras de la ciudad. Calcule el punto de equilibrio de este mercado.
Para esto definimos nuestro sistema de ecuaciones lineales para calcular el punto de intersección,
Igualamos las dos expresiones que definen estas dos rectas, posteriormente despejamos la variable
De esta forma, podemos concluir que la cantidad de equilibrio es y tomando en cuenta que este valor es común en ambas rectas, podemos sustituirlo en las recta de nuestra preferencia para calcular el precio de equilibrio. Sustituyamos el valor
en la ecuación de oferta:
Por lo tanto, concluimos que el punto de equilibrio del mercado es y podemos además, ubicarlo en el plano cartesiano.

Ejemplo 2
Considerando las ecuaciones y
que describen la demanda y la oferta zapatos para dama en una zapatería. Calcule el punto de equilibrio de este mercado.
Para esto definimos nuestro sistema de ecuaciones lineales para calcular el punto de intersección,
Igualamos las dos expresiones que definen estas dos rectas, posteriormente despejamos la variable
De esta forma, podemos concluir que la cantidad de equilibrio es y tomando en cuenta que este valor es común en ambas rectas, podemos sustituirlo en las recta de nuestra preferencia para calcular el precio de equilibrio. Sustituyamos el valor
en la ecuación de oferta:
Por lo tanto, concluimos que el punto de equilibrio del mercado es y podemos además, ubicarlo en el plano cartesiano.

Impuestos Especiales
Como parte de sus políticas económicas, los gobiernos tienden a aplicar impuestos adicionales sobre ciertos artículos con el fin de generar más ingresos, por otra parte, también se dan subsidios a los productores con el fin de que disminuir los precios de ciertos artículos y así los consumidores puedan acceder a dichos artículos con mayor facilidad.
Al estudiar las ecuaciones de demanda y oferta, una vez fijado el precio de un artículo, este precio cuenta con dos interpretaciones dependiendo de cuál de los dos entes involucrados se están estudiando, concretamente, si consideramos el punto equilibrio del mercado, entonces
- Para los consumidores,
denota el precio que pagarán a cambio de
unidades del artículo. Es por esto que en ocasiones se llama precio del demandante y se denota con
o por su nombre en inglés consumer price y se denota con
.
- Para los productores,
denota el precio que recibirán a cambio de
unidades del artículo. Es por esto que en ocasiones se llama precio del oferente y se denota con
o por su nombre en inglés supplier price y se denota con
.
Efecto del impuesto en el equilibrio del mercado
Supongamos que el gobierno impone un impuesto de Perolitos (Ps.) sobre un determinado artículo. Entonces, los productores de este artículo estarán recibiendo
Ps. menos por cada unidad de dicho artículo, esto en comparación con el precio que los consumidores pagan, es decir,
.
Entonces, si originalmente es la ecuación de oferta del artículo, entonces, la ecuación de oferta una vez que se ha fijado el impuesto de
Ps. quedará expresada de la forma
y despejando
, obtenemos que
Gráficamente, se está trasladando la curva de oferta original en unidades hacia arriba en el Eje P, generando así, un nuevo punto de equilibrio de la siguiente forma

Veamos en los siguientes ejemplos, como la imposición de un impuesto afecta el punto de equilibrio del mercado.
Ejemplos
Ejemplo 1
Considerando las ecuaciones y
que describen la demanda y la oferta de zanahorias en una pequeña tienda de verduras de la ciudad. Calcule el punto de equilibrio de este mercado una vez que se ha fijado un impuesto de
Ps. por unidad.
Tomando en cuenta que el precio que se ha fijado un impuesto de Ps. por unidad, entonces tendremos una nueva ecuación de oferta definida por
Contando con esta nueva ecuación de oferta, definimos nuestro sistema de ecuaciones lineales para calcular el punto de intersección,
Igualamos las dos expresiones que definen estas dos rectas, posteriormente despejamos la variable
De esta forma, podemos concluir que la cantidad de equilibrio es y tomando en cuenta que este valor es común en ambas rectas, podemos sustituirlo en las recta de nuestra preferencia para calcular el precio de equilibrio. Sustituyamos el valor
en la ecuación de oferta:
Por lo tanto, concluimos que el punto de equilibrio del mercado es y podemos además, ubicarlo en el plano cartesiano para comparar ambas ecuaciones de oferta.

La curva de oferta una vez que se impone el impuesto es una traslación de la curva de oferta original en unidades hacia arriba en el Eje P. Este aumento en el precio tiene un impacto en la demanda, pues si consideramos el punto de equilibrio original
con el nuevo punto de equilibrio
, notamos que la demanda baja de
unidades a
unidades.
Ejemplo 2
Considerando las ecuaciones y
que describen la demanda y la oferta de zapatos para dama en una zapatería. Calcule el punto de equilibrio de este mercado una vez que se ha fijado un impuesto de
Ps. por unidad.
Tomando en cuenta que el precio que se ha fijado un impuesto de Ps. por unidad, entonces tendremos una nueva ecuación de oferta definida por
Contando con esta nueva ecuación de oferta, definimos nuestro sistema de ecuaciones lineales para calcular el punto de intersección,
Igualamos las dos expresiones que definen estas dos rectas, posteriormente despejamos la variable
De esta forma, podemos concluir que la cantidad de equilibrio es y tomando en cuenta que este valor es común en ambas rectas, podemos sustituirlo en las recta de nuestra preferencia para calcular el precio de equilibrio. Sustituyamos el valor
en la ecuación de oferta:
Por lo tanto, concluimos que el punto de equilibrio del mercado es y podemos además, ubicarlo en el plano cartesiano.

La curva de oferta una vez que se impone el impuesto es una traslación de la curva de oferta original en unidades hacia arriba en el Eje P. Este aumento en el precio tiene un impacto en la demanda, pues si consideramos el punto de equilibrio original
con el nuevo punto de equilibrio
, notamos que la demanda baja de
unidades a
unidades.
Efecto del subsidio en el equilibrio del mercado
Supongamos que el gobierno otorga un subsidio de Perolitos (Ps.) a los productores de determinado artículo. Entonces, los productores de este artículo estarán recibiendo
Ps. más por cada unidad de dicho artículo, esto en comparación con el precio que los consumidores pagan, es decir,
.
Entonces, si originalmente es la ecuación de oferta del artículo, entonces, la ecuación de oferta una vez que se ha otorgado el subsidio de
Ps. quedará expresada de la forma
y despejando
, obtenemos que
Gráficamente, se está trasladando la curva de oferta original en unidades hacia abajo en el Eje P, generando así, un nuevo punto de equilibrio de la siguiente forma

Veamos en los siguientes ejemplos, cómo otorgar un subsidio afecta el punto de equilibrio del mercado.
Ejemplos
Ejemplo 1
Considerando las ecuaciones y
que describen la demanda y la oferta de zanahorias en una pequeña tienda de verduras de la ciudad. Calcule el punto de equilibrio de este mercado una vez que se ha otorgado un subsidio de
Ps. por unidad.
Tomando en cuenta que el precio que se ha otorgado un subsidio de Ps. por unidad, entonces tendremos una nueva ecuación de oferta definida por
Contando con esta nueva ecuación de oferta, definimos nuestro sistema de ecuaciones lineales para calcular el punto de intersección,
Igualamos las dos expresiones que definen estas dos rectas, posteriormente despejamos la variable
De esta forma, podemos concluir que la cantidad de equilibrio es y tomando en cuenta que este valor es común en ambas rectas, podemos sustituirlo en las recta de nuestra preferencia para calcular el precio de equilibrio. Sustituyamos el valor
en la ecuación de oferta:
Por lo tanto, concluimos que el punto de equilibrio del mercado es y podemos además, ubicarlo en el plano cartesiano para comparar ambas ecuaciones de oferta.

La curva de oferta una vez que se otorga el subsidio es una traslación de la curva de oferta original en unidades hacia abajo en el Eje P. Esta disminución en el precio tiene un impacto en la demanda, pues si consideramos el punto de equilibrio original
con el nuevo punto de equilibrio
, notamos que la demanda sube de
unidades a
unidades.
Ejemplo 2
Considerando las ecuaciones y
que describen la demanda y la oferta de zapatos para dama en una zapatería. Calcule el punto de equilibrio de este mercado una vez que se ha otorgado un subsidio de
Ps. por unidad.
Tomando en cuenta que el precio que se ha otorgado un subsidio de Ps. por unidad, entonces tendremos una nueva ecuación de oferta definida por
Contando con esta nueva ecuación de oferta, definimos nuestro sistema de ecuaciones lineales para calcular el punto de intersección,
Igualamos las dos expresiones que definen estas dos rectas, posteriormente despejamos la variable
De esta forma, podemos concluir que la cantidad de equilibrio es y tomando en cuenta que este valor es común en ambas rectas, podemos sustituirlo en las recta de nuestra preferencia para calcular el precio de equilibrio. Sustituyamos el valor
en la ecuación de oferta:
Por lo tanto, concluimos que el punto de equilibrio del mercado es y podemos además, ubicarlo en el plano cartesiano.

La curva de oferta una vez que se otorga el subsidio es una traslación de la curva de oferta original en unidades hacia abajo en el Eje P. Esta disminución en el precio tiene un impacto en la demanda, pues si consideramos el punto de equilibrio original
con el nuevo punto de equilibrio
, notamos que la demanda sube de
unidades a
unidades.


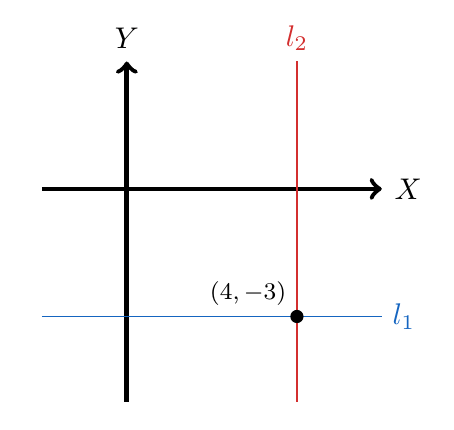
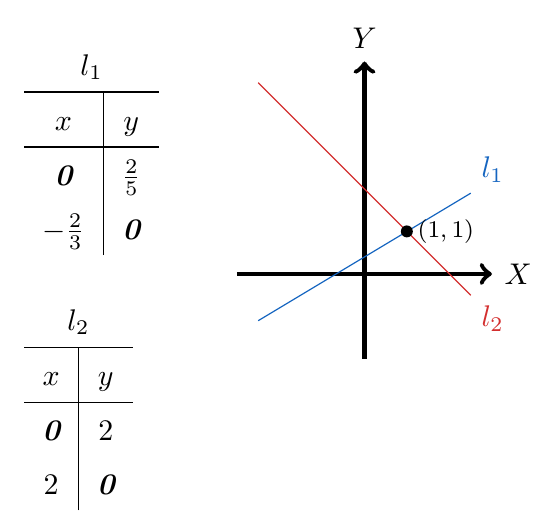
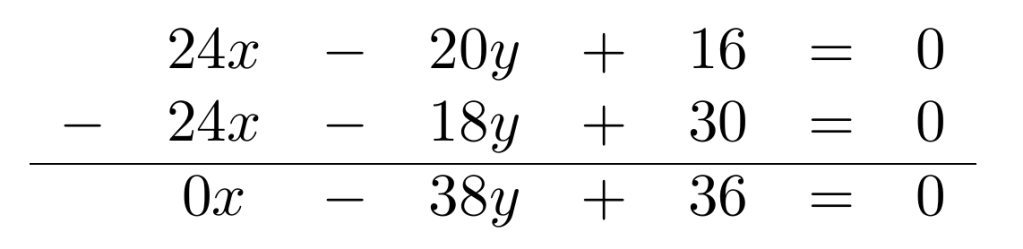
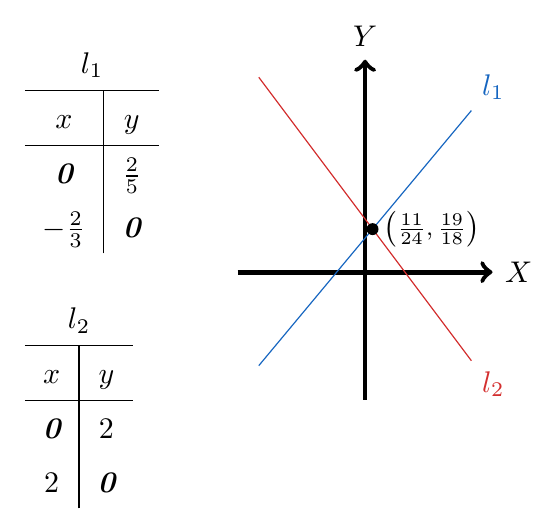
Debe estar conectado para enviar un comentario.