Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.
Verifique si el límite correspondiente es indeterminado o no, en caso de ser indeterminado, aplique que la técnica correspondiente para determinarlo.

Proceda paso a paso, explicando detalladamente cada paso con sus propias palabras.
Verifique si el límite correspondiente es indeterminado o no, en caso de ser indeterminado, aplique que la técnica correspondiente para determinarlo.

Al estudiar el comportamiento de diversas sucesiones, notaremos que existen sucesiones cuyos elementos parecieran acumularse alrededor de un solo punto a medida que crece el valor de y es posible definir formalmente este comportamiento.
También pudiera interesarte
Diremos que una sucesión es convergente, e incluso siendo más específicos, diremos que una sucesión converge hacia un número real
, si
Para todo número , existe un número
tal que si
entonces
En este caso, diremos que es el límite de la sucesión
o que
tiende a
. Esta afirmación se puede escribir con notación matemática para mayor comodidad de la siguiente forma:
En caso contrario, diremos que la sucesión es no-convergente, y más aún, en el caso que la sucesión crezca de forma indefinida, diremos que la sucesión es divergente y lo escribimos de la siguiente forma:
Nuestro propósito será el de determinar el límite de sucesiones, veamos entonces el límite de algunas sucesiones cuyo límite surge de forma intuitiva a partir de su comportamiento.
Determine el límite de la sucesión . Esta es una sucesión constante, así que

Determine el límite de la sucesión . La sucesión de los números reales crece de forma indefinida por lo que está diverge, así que

Determine el límite de la sucesión . La sucesión de proporcionalidad inversa se acerca al cero a medida que crece el valor de
, así que
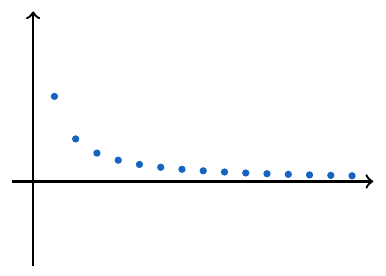
Determine el límite de la sucesión . Esta sucesión alternante no converge pues si consideramos los valores pares de
, la sucesión tiende a uno, por otra parte, si consideramos los valores impares de
, la sucesión tiende a menos uno, así que
no existe.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Si bien en estos ejemplos consideramos sucesiones donde a simple vista podemos estudiar su límite, no siempre será así, por esto es importante destacar que al calcular el límite de operaciones entre sucesiones, podemos definir algunas propiedades. Formalmente, si y
son dos sucesiones cuyos límites son
y
y,
es un número real, entonces

Si bien estas propiedades aligeran el cálculo de límites, estos cálculos no presentará dificultad alguna cuando las sucesiones involucradas son convergentes. Veamos una lista de propiedades para tomar en cuenta cuando alguna de las sucesiones involucradas es divergente.
Si y
son dos sucesiones divergentes;
y
dos sucesiones que tienden a
y a cero respectivamente; entonces consideremos las siguientes operaciones

La resta de infinitos será indeterminada, porque aunque la noción de infinito se usa para denotar números muy grandes, no necesariamente representan un mismo número. También hay que considerar que hay sucesiones que crecen de forma distinta respecto a otras, por lo que al considerar la resta entre ellas, hay que estudiar cual de las dos crece con mayor rapidez.

El producto de cero por infinito será indeterminado. Hay que considerar que hay sucesiones que crecen o decrecen de forma distinta respecto a otras, por lo que al considerar el producto entre ellas, hay que estudiar cual de las dos crece o decrece con mayor rapidez.

La división entre infinitos será indeterminada, porque aunque la noción de infinito se usa para denotar números muy grandes, no necesariamente representan un mismo número. También hay que considerar que hay sucesiones que crecen de forma distinta respecto a otras, por lo que al considerar la división entre ellas, hay que estudiar cual de las dos crece con mayor rapidez. De igual forma, la división de cero entre infinito o infinito entre cero será indeterminada pues se debe considerar que hay sucesiones que crecen o decrecen de forma distinta respecto a otras, por lo que al considerar la división entre ellas, hay que estudiar cual de las dos crece o decrece con mayor rapidez.

Intuitivamente lo que ocurre es que si se multiplica un número mayor que uno por él mismo de forma indefinida, este producto tenderá hacia al infinito; si se multiplica un número mayor que uno por él mismo de forma indefinida de forma indefinida, este producto tenderá hacia cero; si se multiplica el número uno por él mismo de forma indefinida, este producto será siempre igual a uno. Pero cuando una expresión tiende a uno se multiplica por ella misma de forma indefinida, ¿hacia donde tiende? ¿A cero? ¿A uno? ¿A infinito?
De esta lista de operaciones, se han etiquetado con los límites indeterminados, más adelante veremos cuales son las técnicas para determinarlos. Por ahora, veamos con algunos ejemplos como calcular este tipo de límites infinitos que no presentan problemas de determinación.
Considere la sucesión , calcule su límite cuando
tiende a infinito.
Considere la sucesión , calcule su límite cuando
tiende a infinito.
Considere la sucesión , calcule su límite cuando
tiende a infinito.
Considere la sucesión , calcule su límite cuando
tiende a infinito.
Considere la sucesión , calcule su límite cuando
tiende a infinito.
Considere la sucesión , calcule su límite cuando
tiende a infinito.

Consideremos una función lineal definida por una recta , decimos que la pendiente de ésta determina la razón de cambio entre un punto y otro; y es que está definida como el cociente del cambio en el eje Y entre el cambio en el eje X. Formalmente, si
y
son dos puntos de esta recta entonces su razón de cambio desde
hasta
está definida por

De la forma en que hemos definido la razón de cambio para las funciones lineales, permite definir una forma general para la razón de cambio entre cualesquiera dos puntos pues siempre es la misma. Pero, ¿es posible definir una forma general para la razón de cambio para cualquier función?
También pudiera interesarte
Si consideramos cualquier función , es posible estimar la razón de cambio de la misma forma que lo hemos hecho con las funciones lineales, es decir, si
y
son dos puntos de esta recta entonces su razón de cambio desde
hasta
está definida por

Gráficamente podemos notar que hay cierta holgura en nuestra estimación, así que podemos decir que no es precisa. Podemos mejorar esta estimación considerando un punto más cercano a
y así, la razón de cambio está definida por

Incluso, si consideramos un punto aún más cercano a
, la estimación será más precisa y así, la razón de cambio está definida por
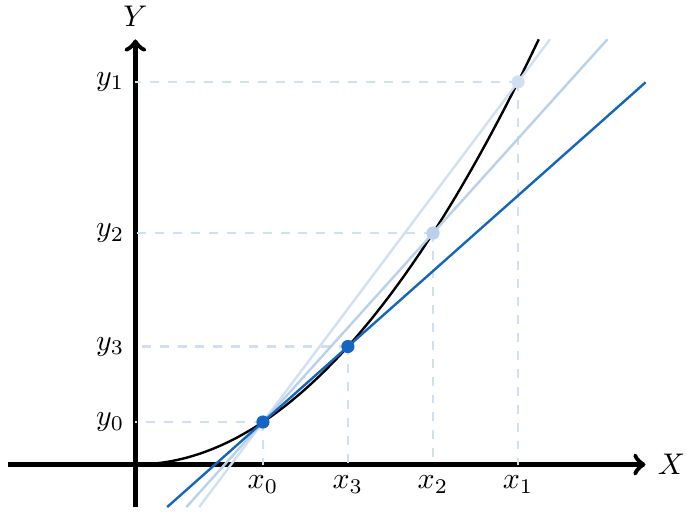
De esta forma podemos notar que mientras más cercano está el punto de , más precisa será nuestra estimación de la razón de cambio. Entonces, consideramos puntos
lo más cercanos posibles recurriendo al cálculo infinitesimal, es decir, al cálculo de límites.
Formalmente, si consideramos el límite cuando tiende a
, entonces la razón de cambio puntual estará dada por
. A este límite lo llamamos derivada de la función
en el punto
y lo denotaremos de la siguiente forma
Geométricamente, representa la pendiente de la recta tangente a la curva definida por en el punto
, es decir, la recta que corta a la curva
únicamente en el punto
de la siguiente forma:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Veamos un ejemplo particular, consideremos la función cuadrática y suponga que queremos calcular su derivada en en
. Entonces, su derivada está definida por el siguiente límite:
Este límite presenta una indeterminación de la forma , así que procedemos a determinarlo considerando que el numerador es una diferencia de cuadrados,
Entonces la razón de cambio puntual de la función cuadrática en el punto es igual a
, geométricamente estamos diciendo que la pendiente de la recta tangente a la curva
en el punto
es igual a
.
Suponga ahora que queremos calcular la derivada en los puntos y
, entonces, ¿debemos calcular el límite cada vez? No necesariamente, pues podemos determinar una fórmula general para calcular la derivada de la función cuadrática en cualquier punto
. Para esto sigamos algunos pasos de forma muy cuidadosa.
Consideremos, una variable auxiliar definida como , esta tenderá a cero cuando
tiende a
, y además, si despejamos
, obtenemos lo siguiente:
Entonces, podemos reescribir la derivada de la función en el punto
de la forma
Entonces, evaluamos la función en y
para luego aplicar producto notable y obtener que
Sacamos como un factor común en el numerador, posteriormente lo simplificamos tomando en cuenta el
que está en el numerador y evaluamos el límite.
Considerando que es cualquier elemento en el dominio de la función cuadrática, podemos establecer una fórmula general para su derivada, es decir, si
entonces su derivada en cualquier punto
de su dominio está definida como
De modo que la derivada de la función en los puntos
y
es
y
, respectivamente.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Es posible establecer fórmulas generales para la derivada de todas las funciones elementales de la misma forma que lo hemos hecho con la función cuadrática y aunque no desarrollaremos los cálculos de forma exhaustiva, podemos hacer una lista de estas derivadas, conocida como la Tabla de Derivadas Elementales

Hasta ahora hemos estudiado el límite de las operaciones básicas entre funciones, sin embargo, si consideramos dos funciones y
, entonces la función
cuando
tiende a infinito debe calcularse tomando tomando en cuenta que
está indeterminado.
La técnica para determinar este tipo de límites parte de la definición del número y es que podemos notar que si hacemos una simple sustitución en el siguiente límite, podemos notar que éste presenta una indeterminación
Afortunadamente, sabemos que éste límite define justamente al número , entonces
Esta fórmula se puede generalizar aún más, pues si consideramos una función que tiende a infinito cuando
tiende a infinito, entonces
De esta forma, al toparnos con la indeterminación puede ser conveniente reescribir la expresión que define la función para obtener el número. Veamos en los siguientes ejemplos como determinar este tipo de límites.
Si consideramos , este límite presenta una indeterminación. Notamos que este límite es levemente diferente al límite que define el número
, así que tomando en cuenta la propiedad de las potencias
entonces podemos reescribir el límite para encontrar la definición del número
de la siguiente forma
De esta forma, notamos que la expresión que está dentro de los corchetes es la definición del número , entonces al calcular el límite obtenemos
Por lo tanto, concluimos que
De forma general, si consideramos una función que tiende a infinito cuando
tiende a infinito, entonces
Si consideramos , este límite presenta una indeterminación. Podemos reescribir de la siguiente forma
De esta forma, notamos que la expresión que está dentro de los corchetes es la definición del número , entonces al calcular el límite obtenemos
Por lo tanto, concluimos que
Si consideramos , este límite presenta una indeterminación. Reescribimos el límite de la siguiente forma
De esta forma, notamos que la expresión que está dentro de los corchetes es la definición del número , entonces al calcular el límite obtenemos
Por lo tanto, concluimos que
Si consideramos , este límite presenta una indeterminación. Reescribimos el límite de la siguiente forma
De forma general, si consideramos dos funciones y
tales que
tiende a infinito cuando
tiende a infinito, entonces
Si consideramos , este límite presenta una indeterminación. Notamos a diferencia del ejemplo anterior, la solución no es tan simple como separar las sumas de fracciones. Así que reescribimos sumando y restando uno en el límite de la siguiente forma
Efectuamos la suma de fracciones para obtener
Ahora multiplicamos y dividimos en el exponente por los factores y
para luego conservar la expresión de nuestro interés,
Aplicamos entonces las propiedades de la potencia de la siguiente manera y obtenemos
Notando que la expresión que está dentro de los corchetes es la definición del número y considerando que en el exponente el polinomio en el numerador y el polinomio en el denominador tienen el mismo grado, el límite será igual al cociente entre sus coeficientes principales, entonces al calcular el límite el resultado será
Por lo tanto, concluimos que
Este tipo de límites no presentan mayor complicación al calcularlos y aunque esta técnica es bastante amplia, encontraremos ocasiones en las que podemos recurrir a métodos más sofisticados pues la técnica que hemos usado hasta ahora puede resultar engorrosa. Veamos entonces, la siguiente serie de igualdades para determinar una fórmula que nos permita calcular este tipo de límites.
Por lo tanto, tenemos que
Veamos en los siguientes ejemplos como determinar este tipo de límites.
Si consideramos , este límite presenta una indeterminación. Entonces, aplicando la fórmula, tenemos que
Entonces, basta con determinar el límite , para esto efectuamos la suma de fracciones para obtener
Posteriormente efectuamos el producto entre los numeradores aplicando la propiedad distributiva, y obtenemos
Y considerando que el polinomio en el numerador y el polinomio en el denominador tienen el mismo grado, el límite será igual al cociente entre sus coeficientes principales, es decir, . Por lo tanto, concluimos que
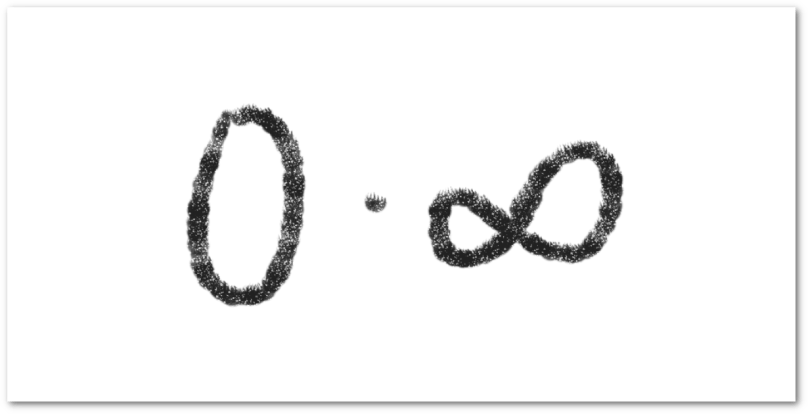
Si y
son dos funciones cuyos límites tienden a infinito y a cero, respectivamente cuando
tiende al infinito, entonces el límite del producto de estas dos funciones presenta una indeterminación. La forma en que se determinan este tipo de límites consiste en reescribir la expresión para obtener una indeterminación de la forma
y usar las técnicas usadas para estos casos. Veamos en los siguientes ejemplos como determinar este tipo de límites
Si consideramos , este presenta una indeterminación. Multiplicamos el producto entre las fracciones y posteriormente aplicamos la técnica que hemos visto anteriormente
Y al evaluar el límite obtenemos
Por lo tanto, concluimos que
Si consideramos , este presenta una indeterminación. Efectuamos la suma de fracciones para obtener
Posteriormente efectuamos el producto entre los numeradores aplicando la propiedad distributiva, y obtenemos
Y considerando que el polinomio en el numerador y el polinomio en el denominador tienen el mismo grado, el límite será igual al cociente entre sus coeficientes principales, por lo tanto, concluimos que
Debe estar conectado para enviar un comentario.