Puntos Críticos
Calcule los puntos críticos de las siguientes funciones y verifique si estos son máximos o mínimos locales. Finalmente, indique cuales son los intervalos de crecimiento y decrecimiento.
Recuerde que los puntos críticos de una función, son aquellos donde
Puntos de Inflexión
Calcule los puntos de inflexión de las siguientes funciones. Finalmente, indique cuales son los intervalos de convexidad (cóncava hacia arriba) y concavidad (cóncava hacia abajo).
Recuerde que los posibles puntos de inflexión de una función, son aquellos donde
$
Bosquejo de Polinomios
Para graficar un polinomio hay que tomar en cuenta varios puntos de interés referentes a la función y sus primeras dos derivadas.
- Para determinar los puntos de corte con el Eje Y, se debe evaluar la función en cero, es decir, calcular
(Sustituir la variable
por cero).
- Para calcular los puntos de corte con el Eje X, se deben calcular los puntos para los cuales la función es igual a cero, es decir, calcular los valores de
para los cuales
(Para esto se puede usar el Método del Discriminante si el polinomio es cuadrático o el Método de Ruffini si es de mayor grado).
- Para determinar los puntos críticos, se deben calcular los puntos para los cuales la derivada de la función es igual a cero, es decir, calcular los valores para los cuales
.
- Para determinar los puntos de inflexión, se deben calcular los puntos para los cuales la segunda derivada de la función es igual a cero, es decir, calcular los valores para los cuales
.
Una vez calculados estos puntos, tome en cuenta que el comportamiento de la función está definido por el signo de la función y sus primeras dos derivadas. Si consideramos un intervalo .
- Si
en
entonces la función está por encima del Eje X.
- Si
en
entonces la función está por debajo del Eje Y.
- Si
en
entonces la función es creciente (
).
- Si
en
entonces la función es decreciente (
).
- Si
en
entonces la función es convexa (
).
- Si
en
entonces la función es cóncava (
).
En los siguientes ejercicios haga un bosquejo de la gráfica de los siguientes polinomios considerando los siguientes pasos:
- Calculamos los puntos de corte con los ejes y estudiamos su positividad (intervalos en los que es positiva o negativa).
- Calculamos los puntos críticos y determinamos su monotonía (intervalos en los que crece o decrece).
- Calculamos los puntos de inflexión y determinamos su concavidad (intervalos en los que es convexa o cóncava).
- Calculamos las imágenes de los puntos de los puntos críticos y de inflexión.
- Esbozar la gráfica.
Optimización de funciones en la economía
Para cada una de las siguientes situaciones, responda las siguientes preguntas:
- ¿Cuáles son valores de
para los cuales la función de ingreso alcanza máximos? ¿Cuáles son esos ingresos máximos?
- ¿Cuáles son valores de
para los cuales la función de costos alcanza mínimos? ¿Cuáles son esos costos mínimos?
- ¿Cuáles son valores de
para los cuales la función de utilidad alcanza máximos? ¿Cuáles son esas utilidades máximas?
- Sea
, la ecuación de oferta de caramelos en una confitería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de piñatas en una piñatería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de carne en una carnicería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de cachitos de jamón y queso en una panadería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de llaves en una cerrajería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de hamburguesas en una hamburguesería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de perros calientes en una perro calentero de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de palmeritas en una panadería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de marcadores en una papelería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de papas fritas en una restaurante de comida rápida de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de colchones en una mueblería de la ciudad y suponga que los costos totales vienen dados de la forma
.
- Sea
, la ecuación de oferta de ropa en una calle de la ciudad y suponga que los costos totales vienen dados de la forma
.

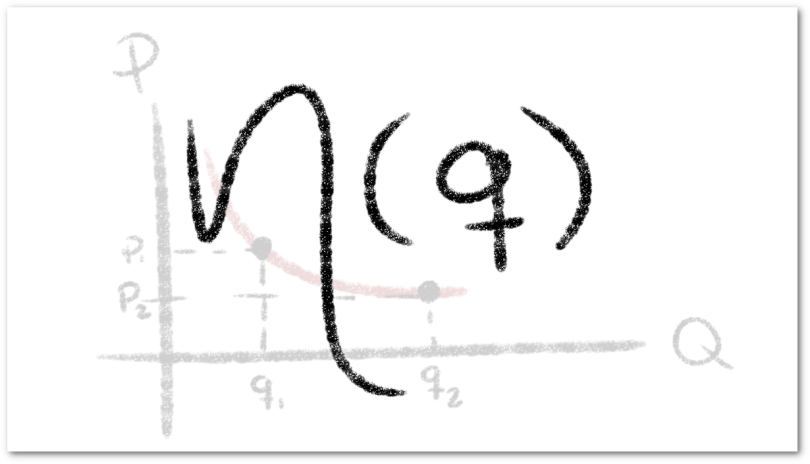
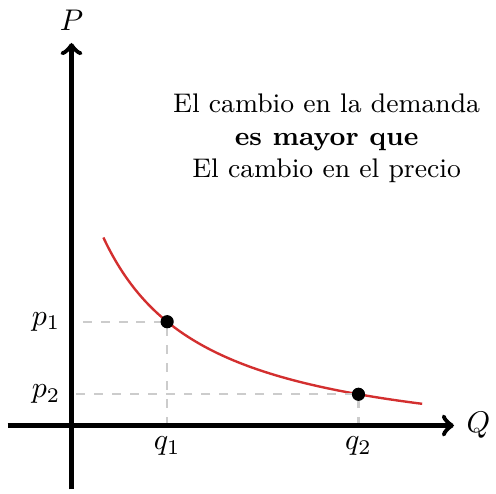
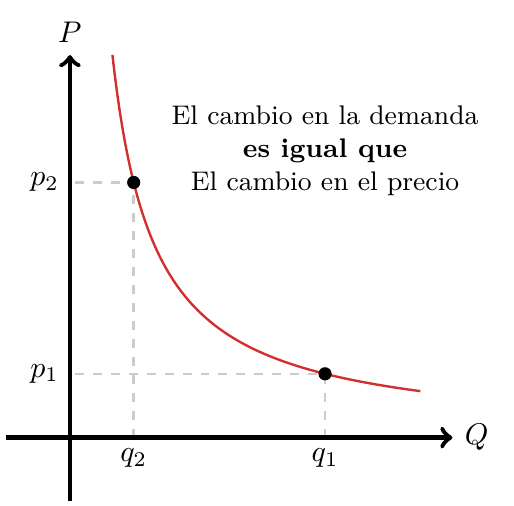
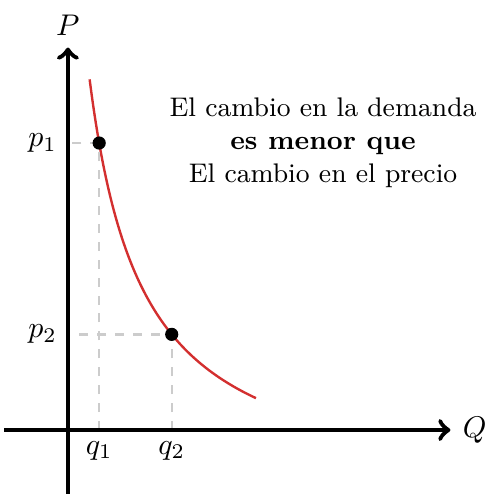
Debe estar conectado para enviar un comentario.