- Forma General de una Ecuación de Bernoulli
- Ejemplos
- Ejemplo 1
Hemos visto que una ecuación expresada de la forma 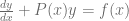 es una ecuación diferencial ordinaria lineal de primer orden no-homogénea y la solución de este tipo de ecuaciones se puede calcular usando el factor integrante.
es una ecuación diferencial ordinaria lineal de primer orden no-homogénea y la solución de este tipo de ecuaciones se puede calcular usando el factor integrante.
También podemos notar que si la ecuación diferencial está expresada de la forma  , se puede reescribir como una ecuación diferencial ordinaria lineal de primer orden homogénea
, se puede reescribir como una ecuación diferencial ordinaria lineal de primer orden homogénea 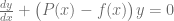 y en consecuencia se puede calcular su solución separando las variables.
y en consecuencia se puede calcular su solución separando las variables.
Veamos a continuación, que este tipo de ecuaciones diferenciales se puede generalizar con el fin de desarrollar un método que nos permita calcular la solución.
También pudiera interesarte
Para cualquier número natural  , diremos que una Ecuación de Bernoulli es una ecuación diferencial ordinaria no lineal expresada de la siguiente forma
, diremos que una Ecuación de Bernoulli es una ecuación diferencial ordinaria no lineal expresada de la siguiente forma

Los casos para los cuales  y
y 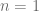 fueron los nombrados en la introducción de esta sección. Así que veremos a continuación, el caso en el que
fueron los nombrados en la introducción de esta sección. Así que veremos a continuación, el caso en el que  . Podemos calcular la solución de este tipo de ecuaciones usando recurriendo a la variable auxiliar
. Podemos calcular la solución de este tipo de ecuaciones usando recurriendo a la variable auxiliar

De esta forma reducimos la ecuación a una ecuación diferencial ordinaria lineal no-homogénea. Veamos con algunos ejemplos calcular la solución de este tipo de ecuaciones diferenciales.
Ejemplos
Ejemplo 1
Calcule la solución de la siguiente ecuación diferencial ordinaria

Lo primero que debemos hacer es estandarizar la ecuación diferencial y para esto dividimos cada uno de los sumandos involucrados por  para obtener
para obtener
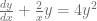
Una vez estandarizada la ecuación diferencial, recurrimos a la variable auxiliar  que en este caso,
que en este caso,  , por lo tango estará expresada como
, por lo tango estará expresada como 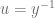 de donde podemos despejar
de donde podemos despejar  elevando a
elevando a 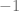 y de forma general, para hacer este despeje, se eleva a
y de forma general, para hacer este despeje, se eleva a  ambos lados de la ecuación para obtener que
ambos lados de la ecuación para obtener que

Será necesario calcular el diferencial de  , así que usando la regla de la cadena concluimos que
, así que usando la regla de la cadena concluimos que
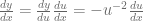
Entonces, sustituimos  y
y  en la ecuación diferencial
en la ecuación diferencial
Posteriormente, estandarizamos esta nueva expresión dividiendo cada uno de los sumandos por 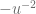 y así, reescribimos la nueva ecuación como una ecuación diferencial ordinaria lineal no-homogénea
y así, reescribimos la nueva ecuación como una ecuación diferencial ordinaria lineal no-homogénea

Identificamos la función 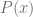 que nos permite calcular el factor integrante de la siguiente manera
que nos permite calcular el factor integrante de la siguiente manera

Entonces, calculamos la solución de la ecuación diferencial
Finalmente, ya que hemos expresado la variable auxiliar  en función de
en función de  , volvemos a sustituirla para obtener
, volvemos a sustituirla para obtener 
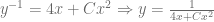
que satisface las siguientes ecuaciones diferenciales. Halle además, la función que satisface el valor inicial donde corresponda.

