- Ecuaciones Diferenciales Ordinarias lineales no-homogéneas con coeficientes constantes
- Método de los Coeficientes Indeterminados
Los métodos para calcular la solución ecuaciones diferenciales ordinarias de orden superior dependen de la forma en que la ecuación esté expresada, considerando el caso lineal, es posible particularizarlo aún más, pues si consideremos una ecuación diferencial de la forma
Las funciones que definen los coeficientes de la ecuación, pueden considerarse como funciones constantes, de forma que la ecuación diferencial queda expresada como
Donde son números reales.
Más aún, será de vital importancia clasificar estas ecuaciones dependiendo del valor de . Diremos que una ecuación de este tipo es no-homogénea si
, y durante esta sección, este es el caso que desarrollaremos.
También pudiera interesarte
Ecuaciones Diferenciales Ordinarias lineales no-homogéneas con coeficientes constantes
Habiendo clasificado las ecuaciones diferenciales ordinarias lineales como homogéneas y no-homogéneas, pudimos establecer un principio (de superposición) que nos determinó la forma en que está expresada la solución general del caso homogéneo. Durante esta sección, podremos generalizar este principio para el caso no-homogéneo. Pero antes debemos precisar algunos elementos.
Consideremos una ecuación diferencial ordinaria lineal no-homogénea de orden expresada de la forma
Definimos su ecuación homogénea asociada, considerando de la siguiente forma
Sabiendo como calcula la solución general esta ecuación homogénea asociada, veremos en el siguiente teorema que esta juega un papel fundamental para poder definir la solución general de la ecuación no-homogénea asociada.
Teorema (Principio de Superposición – Ecuaciones No-Homogéneas)
Si es una solución particular de una ecuación diferencial ordinaria lineal no-homogénea de orden
de la forma
definida en un intervalo ;
conforman un conjunto fundamental de soluciones de la ecuación homogénea asociada en el intervalo
, entonces la siguiente combinación lineal
también es una solución de la ecuación no-homogénea.
De este teorema, diremos que es la solución complementaria y la denotaremos por
. De esta forma, podemos expresar la solución de una ecuación diferencial ordinaria lineal no-homogénea de la siguiente forma
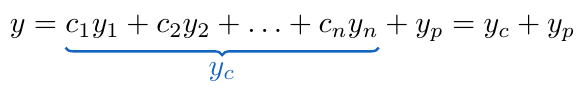
El Principio de Superposición para ecuaciones no-homogéneas puede ser generalizado tomando en cuenta que si tenemos ecuaciones diferenciales ordinarias lineales no-homogéneas de la forma
donde son soluciones particulares correspondientes. Entonces, la suma de todas estas soluciones particulares,
Será una solución particular de la ecuación diferencial ordinaria lineal no-homogénea
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Método de los Coeficientes Indeterminados
Conociendo esta última generalización, veamos un método que se basa en intuir cómo debería ser la solución de una ecuación diferencial ordinaria lineal no-homogénea fijándonos en la forma en que está expresada la función . Desarrollaremos este método para tres formas básicas de la función
.
Forma Polinómica
Si es un polinomio de grado
expresado de la forma
entonces una solución particular debería tener también forma polinómica pues derivando polinomios, obtenemos polinomios, es decir, de la forma
Forma Exponencial
Si es una función exponencial expresada de la forma
entonces una solución particular debería tener también forma exponencial pues derivando funciones exponenciales, obtenemos funciones exponenciales, es decir, de la forma
De forma general, si es una función exponencial expresada de la forma
entonces una solución particular debería tener también forma polinómica pues derivando funciones exponenciales, obtenemos funciones exponenciales, es decir, de la forma
Forma Trigonométrica
Si está expresada como la suma de senos y cosenos de la forma
entonces una solución particular debería tener también forma de suma de senos y cosenos pues \emph{derivando senos y cosenos, obtenemos senos y cosenos}, es decir, de la forma
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Estos tres casos pueden combinarse ya sea con sumándolos o multiplicándolos entre sí, de esta forma podemos ampliar el espectro de soluciones que podemos considerar para ecuaciones diferenciales ordinarias lineales no-homogéneas con coeficientes constantes.
Para entender como aplicar este método, veamos algunos ejemplos que ilustrarán con precisión el desarrollo del mismo.
Ejemplos
Ejemplo 1
Calcule la solución de la siguiente ecuación diferencial ordinaria lineal homogénea con coeficientes constantes
Antes de abordar esta ecuación, debemos recordar que la solución general de este tipo de ecuaciones se expresa como
Como primer paso debemos calcular la solución complementaria . Considerando la ecuación homogénea asociada
, podemos expresar su ecuación auxiliar
y calcular su solución utilizando el método del discriminante:
Por lo tanto, expresamos la solución complementaria de la siguiente manera:
Como segundo paso, debemos notar que en la ecuación diferencial planteada, , es una función polinómica de segundo grado. Así, intuitivamente nuestra solución particular debería tener la siguiente forma
Nuestro propósito será el de hallar ,
y
y para esto sustituimos
en la ecuación original pues esta debe satisfacer la igualdad. Entonces
Sustituimos en la ecuación diferencial que hemos planteado originalmente para obtener
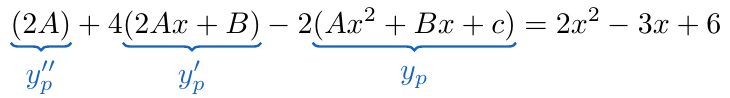
Considerando únicamente la expresión que está del lado izquierdo de la ecuación, expandimos distribuyendo los factores involucrados y posteriormente agrupamos los elementos que multiplican a ,
y los términos independientes.
Esta última expresión debe ser exactamente igual a , entonces los coeficientes correspondientes también deben ser exactamente iguales, por lo que planteamos el siguiente sistema de ecuaciones lineales:
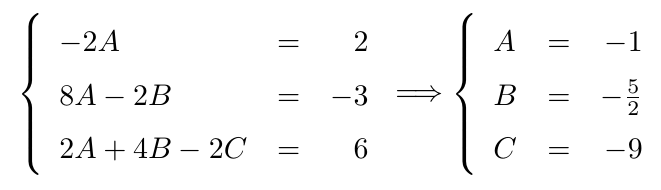
Así, nuestra solución particular viene dada por
Finalmente, la solución general está expresada de la siguiente manera:
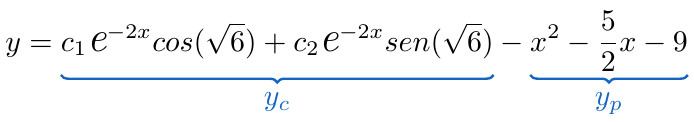
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplo 2
En este ejemplo veremos que debemos ser cuidadosos al calcular la solución pues la escogencia intuitiva pudiera no ser la más correcta, así que debemos recurrir a otra escogencia más general. Calcule la solución de la siguiente ecuación diferencial ordinaria lineal homogénea con coeficientes constantes
Antes de abordar esta ecuación, debemos recordar que la solución general de este tipo de ecuaciones se expresa como
Como primer paso debemos calcula la solución complementaria . Considerando la ecuación homogénea asociada
, podemos expresar su ecuación auxiliar
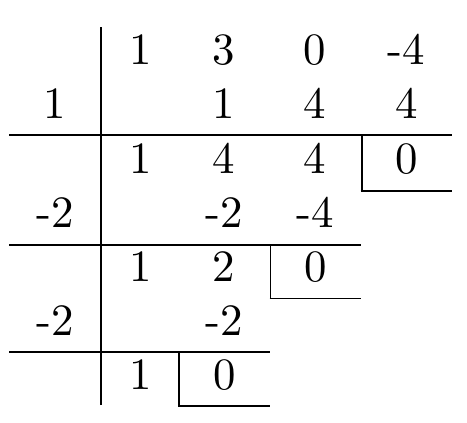
y calcular su solución utilizando el método del discriminante una vez que hemos factorizado:
Por lo tanto, expresamos la solución complementaria de la siguiente manera:
Es decir,
Como segundo paso, debemos notar que en la ecuación diferencial planteada, , una función exponencial más una función polinómica de primer grado. Así, intuitivamente nuestra solución particular debería tener la siguiente forma
Nuestro propósito será el de hallar ,
y
y para esto sustituimos
en la ecuación original pues esta debe satisfacer la igualdad. Entonces
Sustituimos en la ecuación diferencial que hemos planteado originalmente para obtener
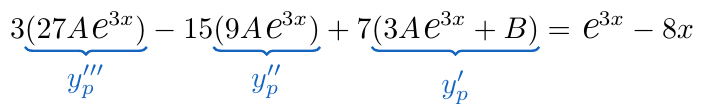
Considerando únicamente la expresión que está del lado izquierdo de la ecuación, efectuamos los factores involucrados y posteriormente agrupamos los elementos que multiplican a y los términos independientes.
Esta última expresión debe ser exactamente igual a , entonces los coeficientes correspondientes también deben ser exactamente iguales, por lo que planteamos el siguiente sistema de ecuaciones lineales:
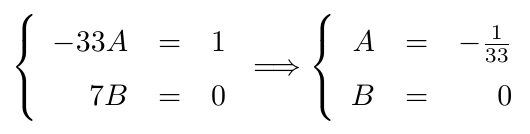
Sin embargo, estos coeficientes no proveen una solución pues
y al plantear de esta forma la solución particular, no se satisface la igualdad por lo tanto será necesario replantearla.
La teoría sugiere aumentar en un grado la función donde se presenta el problema, por lo tanto, en este caso aumentaremos en un grado el elemento polinómico de la solución particular. Entonces, si consideramos , tenemos que
Sustituimos estas nuevas expresiones en la ecuación diferencial que hemos planteado originalmente para obtener
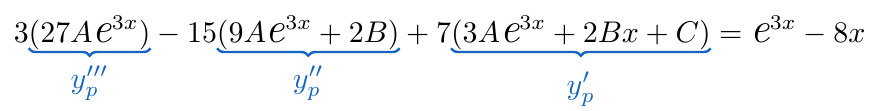
Considerando únicamente la expresión que está del lado izquierdo de la ecuación, efectuamos los factores involucrados y posteriormente agrupamos los elementos que multiplican a y los términos independientes.
Esta última expresión debe ser exactamente igual a , entonces los coeficientes correspondientes también deben ser exactamente iguales, por lo que planteamos el siguiente sistema de ecuaciones lineales:
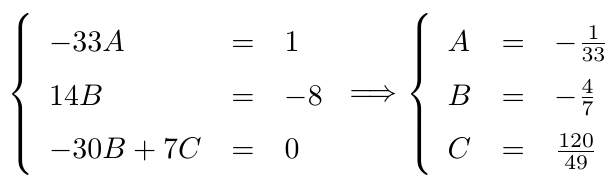
Así, nuestra solución particular viene dada por
Finalmente, expresamos nuestra solución.
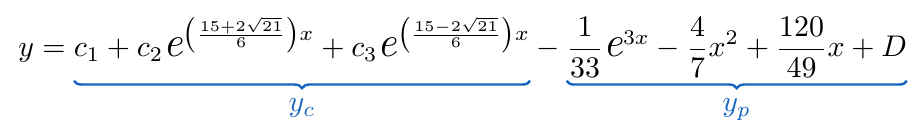

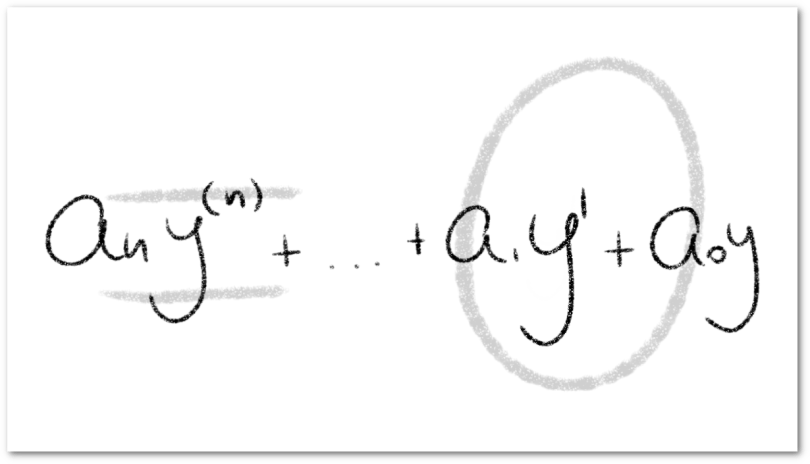
Debe estar conectado para enviar un comentario.