- Función Constante
- Función Identidad
- Función Cuadrática
- Función de Proporcionalidad Inversa
- Función Raíz Cuadrada
- Función Raíz Cúbica
- Función Exponencial
- Función Logarítmica
Para graficar funciones no es siempre es necesario un software o apps especializadas en matemáticas pues siempre que se disponga de una conexión a internet se pueden generar gráficas de funciones elementales (e incluso funciones no elementales) usando Google de forma muy sencilla, para esto se escribe el siguiente comando «graph for» y seguidamente de la función que se desea graficar en el campo de búsqueda, sin embargo, estas funciones se deben escribir con una sintaxis muy particular.
Función Constante
Para graficar la función constante  donde
donde  es un número real, se debe escribir
es un número real, se debe escribir
graph for c
Por supuesto, sustituyendo  por el valor deseado. Si se desea graficar la función
por el valor deseado. Si se desea graficar la función  , se debe escribir lo siguiente en el campo de búsqueda
, se debe escribir lo siguiente en el campo de búsqueda
graph for 3
Función Identidad
Para graficar la función identidad 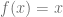 , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for x
Nota: Usted puede hacer «zoom in» y «zoom out» para ver detalles de la gráfica en los puntos que desee.
Función Cuadrática
Para graficar la función cuadrática se debe usar el circunflejo para denotar qué número está en el exponente, usando el símbolo «^». Si se desea graficar la función cuadrática 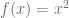 , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for x^2
De esta forma se puede graficar funciones como la cuadrática, la cúbica, y en general cualquier función de la forma 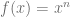 donde
donde  es un número natural.
es un número natural.
Función de Proporcionalidad Inversa
El producto se denota con un asterisco «*» y la división se denota con el slash «/», entonces si se desea graficar la función de proporcionalidad inversa  , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for 1/x
Notemos que con esta sintaxis y la aprendida con la función cuadrática, se puede graficar cualquier función de la forma  donde
donde  es un número natural mayor que 1.
es un número natural mayor que 1.
Función Raíz Cuadrada
Para graficar la función raíz cuadrada 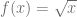 se debe usar una instrucción especial para denotar la raíz cuadrada de una variable, esta es sqrt y significa «Square Root» que se traduce precisamente del inglés como «Raíz Cuadrada», este es el estándar para denotar la raíz cuadrada en cualquier entorno matemático con el que se trabaje. Si se desea graficar la función raíz cuadrada, se debe escribir lo siguiente en el campo de búsqueda:
se debe usar una instrucción especial para denotar la raíz cuadrada de una variable, esta es sqrt y significa «Square Root» que se traduce precisamente del inglés como «Raíz Cuadrada», este es el estándar para denotar la raíz cuadrada en cualquier entorno matemático con el que se trabaje. Si se desea graficar la función raíz cuadrada, se debe escribir lo siguiente en el campo de búsqueda:
graph for sqrt(x)
Función Raíz Cúbica
Recuerde que se puede reescribir la función raíz cuadrada de  como
como  . Se puede generalizar este hecho para graficar cualquier función que involucre una raíz, por ejemplo, si se desea graficar la función raíz cúbica
. Se puede generalizar este hecho para graficar cualquier función que involucre una raíz, por ejemplo, si se desea graficar la función raíz cúbica  , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for x^(1/3)
Función Exponencial
Si se desea graficar la función exponencial  , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for e^x
Función Logarítmica
Para graficar la función logarítmica se debe usar una instrucción especial para denotar el logaritmo de una variable, esta es log, este es el estándar para denotar el logaritmo base 10 en cualquier entorno matemático con el que se trabaje. Si se desea graficar la función logarítmica  , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for log(x)
Particularmente nos puede interesar el logaritmo neperiano y para este se usa la instrucción ln, este es el estándar para denotar el logaritmo neperiano en cualquier entorno matemático con el que se trabaje. Si se desea graficar la función logaritmo neperiano  , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for ln(x)
Se pueden graficar más de dos funciones o más al mismo tiempo, separando las mismas con comas. Si queremos comparar las funciones  y
y  en mismo gráfgico, se debe escribir lo siguiente en el campo de búsqueda:
en mismo gráfgico, se debe escribir lo siguiente en el campo de búsqueda:
graph for log(x), ln(x)
Supongamos ahora que queremos graficar las funciones identidad y cuadrática al mismo tiempo, se debe escribir lo siguiente en el campo de búsqueda:
graph for x, x^2
Notando que las funciones son graficadas con colores distintos para facilitar su distinción.
Una vez conociendo todo lo anterior podemos graficar transformaciones de funciones elementales. Por ejemplo el valor absoluto se denota como abs. Entonces para graficar las siguientes funciones  ,
,  y
y  , se debe escribir lo siguiente en el campo de búsqueda:
, se debe escribir lo siguiente en el campo de búsqueda:
graph for (x-2)^2-1, 1/(-x-2)+1, abs(ln(x+1))
También se pueden graficar funciones no elementales. Al usar aplicaciones más sofisticadas para hacer gráficos de funciones, la sintaxis usada en el buscador de google es muy parecida, entonces al dominar este tipo de escritura, no se presentará mayor dificultad al usar otra plataforma, aplicación o calculadoras avanzadas en general.
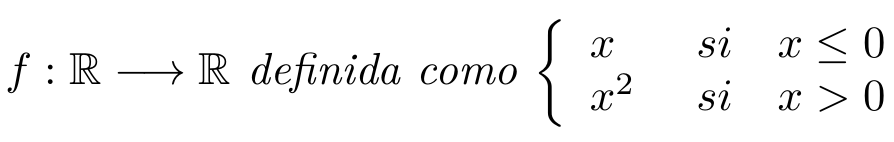

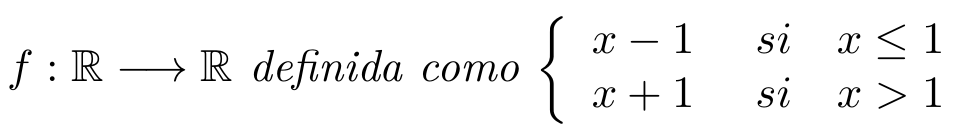
que la imagen no está incluida en el extremo y denotamos con un punto relleno
que la imagen sí está incluida en el extremo de la siguiente manera:

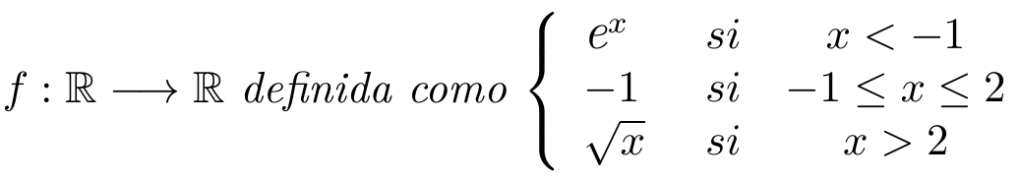

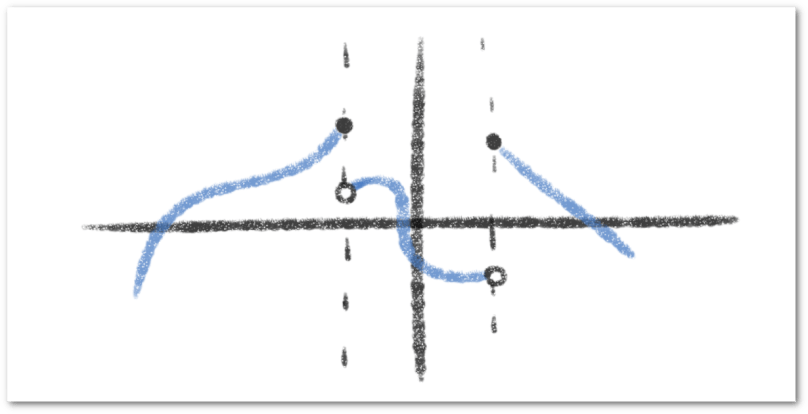


























Debe estar conectado para enviar un comentario.