Categoría: Matemáticas

Suma de Fracciones

Anthonny Arias-García6 comentarios

Sean a, b, c y d números enteros tales que b y d son distintos de cero. Definimos la suma de las fracciones \frac{a}{b} más \frac{c}{d}, sumando el producto de a por d más el producto de b por c y dividiendo todo esto entre el producto de b por d, de la siguiente forma:

Una forma fácil de recordar esta suma para aquellos a los que se les presenta dificultad, es notar que al efectuar las operaciones se hace la forma de una copa tal como veremos a continuación

Veamos con algunos ejemplos como efectuar la suma entre fracciones.

Ejemplos

Ejemplo 1

Efectúe la suma de \frac{1}{2} más \frac{3}{4}.

\frac{1}{2} + \frac{3}{4} = \frac{1 \cdot 4 + 2 \cdot 3}{2 \cdot 4} = \frac{4 + 6}{8} = \frac{10}{8} = \frac{5}{4}

Ejemplo 2

Efectúe la suma de \frac{7}{3} más \frac{2}{5}.

\frac{7}{3} + \frac{2}{5} = \frac{7 \cdot 5 + 3 \cdot 2}{3 \cdot 5} = \frac{35 + 6}{15} = \frac{41}{15}

Ejemplo 3

Efectúe la suma de 1 más \frac{4}{9}. Para efectuar esta suma debemos notar primero que el número 1 se puede escribir como la fracción \frac{1}{1}, entonces tenemos que

\frac{1}{1} + \frac{4}{9} = \frac{1 \cdot 9 + 1 \cdot 4}{1 \cdot 9} = \frac{9 + 4}{9} = \frac{13}{9}

Ejemplo 4

Efectúe la suma de \frac{3}{11} más 6. Para efectuar esta suma debemos notar primero que el número 6 se puede escribir como la fracción \frac{6}{1}, entonces tenemos que

\frac{3}{11} + \frac{6}{1} = \frac{3 \cdot 1 + 11 \cdot 6}{11 \cdot 1} = \frac{3 + 66}{11} = \frac{69}{11}

Fracciones

Anthonny Arias-García6 comentarios
  1. Propiedades de las Fracciones
  2. Ley de los Signos para las Fracciones
  3. Fracciones propias e impropias
    1. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2
      3. Ejemplo 3
      4. Ejemplo 4
      5. Ejemplo 5
      6. Ejemplo 6
      7. Ejemplo 7
      8. Ejemplo 8
  4. Fracciones Mixtas
    1. Ejemplos
      1. Ejemplo 9
      2. Ejemplo 10
      3. Ejemplo 11
      4. Ejemplo 12
      5. Ejemplo 13

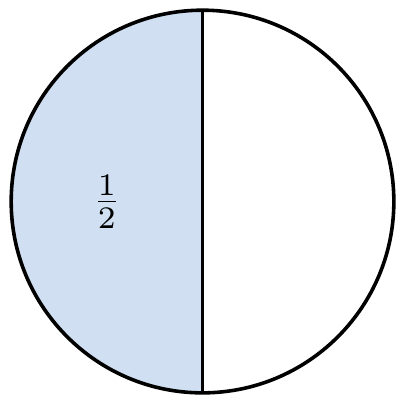
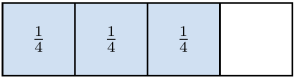
Las fracciones son una forma alternativa para denotar la división entre dos números y generalmente se usan para expresar proporciones, por ejemplo, para expresar las tres cuartas partes de una cantidad escribimos 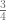\frac{3}{4} o por ejemplo, para denotar la mitad de una torta simplemente escribimos \frac{1}{2}. Es posible representar las fracciones de forma gráfica para facilitar su entendimiento.

Fracciones | totumat.com
Fracciones | totumat.com

Formalmente, si consideremos dos números enteros a y b \neq 0, entonces diremos que a es el numerador de la fracción y b es el denominador de la fracción, y así, la división a \div b estará representada por la siguiente expresión

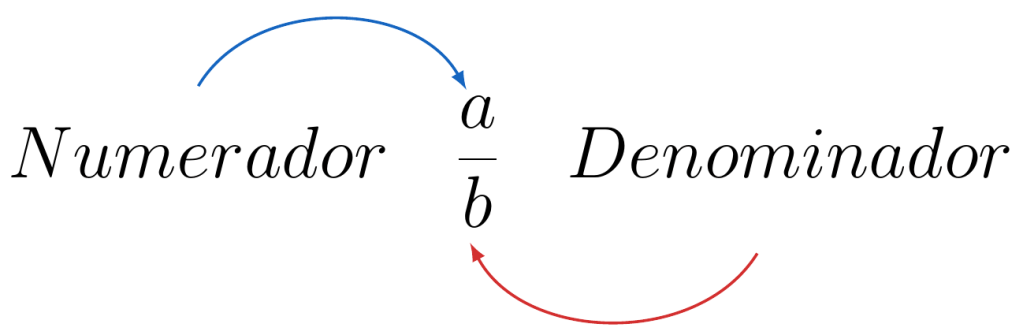
Fracciones | totumat.com

La raya entre ambos números usualmente es llamada raya de fracción, el número sobre la raya se conoce como numerador y el número bajo la raya se conoce como denominador.

También pudiera interesarte

Propiedades de las Fracciones

Cuando trabajamos con fracciones, encontraremos expresiones muy particulares que podemos identificar cuando queremos simplificar operaciones matemáticas. Consideremos a un número entero distinto de cero y veamos a continuación cuales son estas fracciones.

Uno dividio entre uno, es igual a uno. De forma general, si consideramos cualquier número real distinto de cero, la división de este número por él mismo, es igual a uno, entonces,

\dfrac{1}{1} = 1.

\dfrac{a}{a} = 1.

Cualquier número entero se puede expresar como la división de él mismo con uno, esta información será últil cuando se nos presenten operaciones entre números expresados en fracciones y números enteros.

\dfrac{a}{1} = a.

Al dividir cero por cualquier número real distinto de cero, el resultado siempre será el mismo, cero.

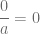
\dfrac{0}{a} = 0

Por el contrario, si tomamos cualquier número real, este no podrá ser dividio por cero pues esta operación no está definida, es decir, la división por cero no está definida.

\dfrac{a}{0}

no está definida.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ley de los Signos para las Fracciones

Ya que las fracciones representan divisiones, podemos también establecer la ley de los signos para la división, si a y b son números enteros positivos tal que b es distinto de cero, entonces

El resultado de dividir un número positivo entre un número positivo, es positivo.

\displaystyle \frac{a}{b} = \frac{a}{b}

El resultado de dividir un número positivo entre un número negativo, es negativo.

\displaystyle \frac{-a}{b} = -\frac{a}{b}

El resultado de dividir un número negativo entre un número positivo, es negativo.

\displaystyle \frac{a}{-b} = -\frac{a}{b}

El resultado de dividir un número negativo entre un número negativo, es positivo.

\displaystyle \frac{-a}{-b} = \frac{a}{b}

La ventaja en el uso de las fracciones es que nos proveen rigidez en los resultados y así evitamos errores de aproximación o redondeo al efectuar divisiones, es por esto que es necesario dominar las operaciones de suma, resta, multiplicación y división entre las fracciones.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Fracciones propias e impropias

Una forma de clasificar las fracciones es considerando el tamaño de su numerador y su denominador, pues estos determinarán la porción que realmente representan. Si a y b son dos enteros tal que b \neq 0, tenemos que

  • Si a < b, diremos que la fracción es \frac{a}{b} es propia, es decir, si el numerador es menor que el denominador.
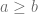  • Si a \geq b, diremos que la fracción es \frac{a}{b} es impropia, es decir, si el numerador es mayor o igual que el denominador.

Para aclarar esta idea, veamos algunos ejemplos.

Ejemplos

Ejemplo 1

La fracción \frac{1}{2}, es una fracción propia, pues su numerador es menor que su denominador.

Ejemplo 2

La fracción \frac{7}{15}, es una fracción propia, pues su numerador es menor que su denominador.

Ejemplo 3

La fracción 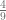\frac{4}{9}, es una fracción propia, pues su numerador es menor que su denominador.

Ejemplo 4

La fracción 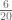\frac{6}{20}, es una fracción propia, pues su numerador es menor que su denominador.

Ejemplo 5

La fracción \frac{5}{3}, es una fracción impropia, pues su numerador es mayor que su denominador.

Ejemplo 6

La fracción 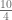\frac{10}{4}, es una fracción impropia, pues su numerador es mayor que su denominador.

Ejemplo 7

La fracción \frac{20}{12}, es una fracción impropia, pues su numerador es mayor que su denominador.

Ejemplo 8

La fracción 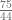\frac{75}{44}, es una fracción impropia, pues su numerador es mayor que su denominador.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Fracciones Mixtas

Al leer una receta de cocina es común encontrarse con medidas para los ingredientes como una taza y media de azúcar o, es por esto que podemos encontrar recipientes con medidas de 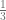\frac{1}{2}, \frac{1}{3}, \frac{1}{4} o \frac{1}{8}. Esto también ocurre cuando se compran alimentos que deben ser pesados, como un kilo y cuarto de queso o tres kilos y medios de carne.

Las fracciones son ideales para expresar este tipo de medidas, justamente están diseñadas para medir porciones, por ejemplo, para escribir una taza y media se puede escribir 1 + \frac{1}{2} que a su vez es igual a \frac{3}{2}. Sin embargo, la forma en que se escriben pueden no presentar comodidad o claridad en la práctica, es por esto que se definen las fracciones mixtas (o números mixtos), entonces, que en vez de escribir 1 + \frac{1}{2}, se escribe

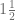
1\tfrac{1}{2}

De esta forma, definimos las fracciones mixtas para separar la parte entera de su parte no entera, esta última usualmente representada con una fracción propia. Cualquier fracción mixta se puede reescribir como una fracción impropia, pues si a, b y c son números enteros positivos, entonces la siguiente fracción mixta

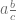
a\tfrac{b}{c}

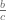se reescribe como una fracción impropia sumando a con \frac{b}{c}, es decir,

a + \frac{b}{c} = \frac{a \cdot c + b}{c}

Veamos algunos ejemplos de cómo reescribir fracciones mixtas.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ejemplos

Ejemplo 9

Reescriba la fracción mixta 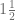1\tfrac{1}{2} como una fracción impropia.

1\tfrac{1}{2} = 1 + \frac{1}{2} = \frac{1 \cdot 2 + 1}{2} = \frac{3}{2}

Ejemplo 10

Reescriba la fracción mixta 1\tfrac{1}{8} como una fracción impropia.

1\tfrac{1}{8} = 1 + \frac{1}{8} = \frac{1 \cdot 8 + 1}{2} = \frac{9}{2}

Ejemplo 11

Reescriba la fracción mixta 2\tfrac{3}{4} como una fracción impropia.

2\tfrac{3}{4} = 2 + \frac{3}{4} = \frac{2 \cdot 4 + 3}{4} = \frac{11}{4}

Ejemplo 12

Reescriba la fracción mixta 2\tfrac{3}{4} como una fracción impropia.

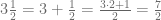
3\tfrac{1}{2} = 3 + \frac{1}{2} = \frac{3 \cdot 2 + 1}{2} = \frac{7}{2}

Ejemplo 13

Reescriba la fracción mixta 5\tfrac{9}{16} como una fracción impropia.

5\tfrac{9}{16} = 5 + \frac{9}{16} = \frac{5 \cdot 16 + 9}{16} = \frac{89}{16}

Curvas de Indiferencia y TMS

Anthonny Arias-García1 comentario

En la economía, la utilidad estudia el nivel de satisfacción de un individuo respecto a la forma en que este clasifica distintas situaciones, sin embargo, este tipo de funciones no se pueden cuantificar de forma rigurosa pues la satisfacción es algo muy subjetivo ya que la utilidad de una persona no sólo depende de los bienes materiales que consume, sino también de sus actitudes psicológicas, de las presiones de su grupo social, de sus experiencias personales y del entorno cultural en general según Walter Nicholson en su libro de Teoría Microeconómica, Principios básicos y ampliaciones, es por esto que se restringe el estudio de este tipo de funciones a variables que se puedan medir como las cantidades relativas de alimento, horas de trabajo semanales o tasas fiscales, las variables que no podemos medir se suponen como constantes, esto se le llama en los libros de texto económicos ceteris paribus.

También pudiera interesarte

Consideremos el caso particular en que una vez presentados n bienes distintos, un individuo debe escoger cantidades x_1, x_2, \ldots, x_n de dichos bienes. Entonces, representaremos la forma en que este individuo clasifica estos bienes definiendo una función de utilidad de la siguiente forma:

U(x_1, x_2, \ldots, x_n)

Cuando sólo se toman en consideración dos bienes, entonces la función de utilidad se expresa sólo para la cantidad de estos dos bienes x y y:

U(x,y)

La curva de nivel U(x,y) = U_0 representa todas las combinaciones de x y y que proveen al individuo un nivel de satisfacción igual a U_0. Esta curva de nivel se llama curva de indiferencia pues al ellas representar todas las combinaciones de las canastas del mercado que proveen al individuo el mismo nivel de satisfacción, este se mostrará indiferente entre una canasta y otra. De forma general, si la función U(x,y) es una función de Cobb-Douglas, su gráfica estará representada de la siguiente forma:

La curva de indiferencia además de mostrar las combinaciones de los bienes x y y, nos permiten observar que en que medida un individuo está dispuesto a intercambiar los bienes para obtener el mismo nivel de satisfacción. De forma que si tiene las cantidades x_0 y y_0 de un bien, la cantidad de unidades de y que intercambia para obtener una unidad de x está definida como la tasa marginal de sustitución (TMS) y está determinada por la pendiente negativa de la curva U_0 en el punto (x_0,y_0), es decir,

TMS = -\frac{dy}{dx}

Calculada a partir de la función implícita U(x,y)=U_0.

¿Cómo calcular la TMS?

Es posible determinar la tasa marginal de sustitución calculando derivadas parciales pues si tomamos en cuenta que el diferencial de la función de utilidad está dada por dU = \frac{\partial U}{\partial x} dx + \frac{\partial U}{\partial y} dy, entonces el diferencial de la curva de nivel U_0 será

\frac{\partial U}{\partial x} dx + \frac{\partial U}{\partial y} dy = 0 \ \Longrightarrow \ \frac{\partial U}{\partial y} dy = -\frac{\partial U}{\partial x} dx

A partir de esta igualdad, podemos obtener la derivada \frac{dy}{dx} haciendo un abuso de la notación para despejar los diferenciales de x y y de la siguiente forma

\dfrac{dy}{dx} = -\dfrac{\frac{\partial U}{\partial x}}{\frac{\partial U}{\partial y}} \ \Longrightarrow \ -\dfrac{dy}{dx} = \dfrac{\frac{\partial U}{\partial x}}{\frac{\partial U}{\partial y}} \ \Longrightarrow \ TMS = \dfrac{\frac{\partial U}{\partial x}}{\frac{\partial U}{\partial y}}

Ejemplos

Reduzcamos una situación en la que un individuo de la sociedad sólo puede dedicar su tiempo a dos usos respecto al mercado: horas de trabajo y horas de no trabajo.

Denotaremos las horas de trabajo con la variable l (labor en inglés) y si por cada hora de trabajo obtiene un ingreso de w, entonces, considerando que este individuo puede adquirir bienes si trabaja, definimos la variable consumo c = l \cdot w.

Definiremos las horas de no trabajo como horas de ocio y las denotaremos con la variable h, estas representan las horas que dedica a trabajar en casa (no en el mercado), ver televisión o navegar en las redes sociales.

Suponga que las preferencias de este individuo están determinadas a través de la siguiente función de utilidad:

U(C,H)=3\sqrt[5]{C^2} \cdot \sqrt[5]{H^3}

Para determinar la TMS. Debemos calcular ambas funciones de utilidad marginal. Previamente, debemos notar que U(C,H)=3\sqrt[5]{C^2} \cdot \sqrt[5]{H^3} = 3 C^{\frac{2}{5}} \cdot H^{\frac{3}{5}}, por lo tanto

\frac{\partial U}{\partial C} = 3 \cdot \frac{2}{5} \cdot C^{-\frac{3}{5}} \cdot H^{\frac{3}{5}} = \frac{6}{5} \cdot \frac{H^{\frac{3}{5}}}{C^{\frac{3}{5}}} = \frac{6}{5} \cdot \frac{\sqrt[5]{H^3}}{\sqrt[5]{C^3}}

\frac{\partial U}{\partial H} = 3 \cdot \frac{3}{5} \cdot H^{-\frac{2}{5}} \cdot C^{\frac{2}{5}} = \frac{9}{5} \cdot \frac{C^{\frac{2}{5}}}{H^{\frac{2}{5}}} = \frac{9}{5} \cdot \frac{\sqrt[5]{C^2}}{\sqrt[5]{H^2}}

Luego,

TTS = \dfrac{\frac{\partial U}{\partial C}}{\frac{\partial U}{\partial H}} = \frac{ \frac{6}{5} \cdot \frac{\sqrt[5]{H^3}}{\sqrt[5]{C^3}}}{\frac{9}{5} \cdot \frac{\sqrt[5]{C^2}}{\sqrt[5]{H^2}}} = \frac{2}{3}\frac{H}{C}

Curva Isocuanta y TTS

Anthonny Arias-García1 comentario

Si una empresa decide fijar su producción en una cantidad P_0, una vez que ha determinado que su función de producción está dada de la forma P(L,K), podemos representar mediante una curva de nivel todas las combinaciones posibles de trabajo y capital que mantendrán la producción fija en P_0. Esta curva de nivel será llamada Curva Isocuanta (igual cantidad) y de forma general, si la función P(L,K) es una función de Cobb-Douglas, su gráfica estará definida de la siguiente forma:

También pudiera interesarte

La curva isocuanta además de mostrar las combinaciones de los bienes L y K, nos permiten observar que en que medida se puede intercambiar capital por trabajo manteniendo el mismo nivel de producción. De forma que si se trabajan L_0 horas semanales y se invierten K_0 unidades de capital, la cantidad de unidades de K que se intercambian por unidades de trabajo L está definida como la tasa técnica de sustitución (TTS) y está determinada por la pendiente negativa de la curva P_0 en el punto (L_0,K_0), es decir,

TTS = -\frac{dL}{dK}

Calculada a partir de la función implícita P(L,K)=P_0.

¿Cómo calcular la TTS?

Es posible determinar la tasa marginal de sustitución calculando derivadas parciales pues si tomamos en cuenta que el diferencial de la función de producción está dada por dP = \frac{\partial P}{\partial L} dL + \frac{\partial P}{\partial K} dK, entonces el diferencial de la curva de nivel P_0 será

\frac{\partial P}{\partial L} dL + \frac{\partial P}{\partial K} dK = 0 \ \Longrightarrow \ \frac{\partial P}{\partial K} dK = -\frac{\partial P}{\partial L} dL

A partir de esta igualdad, podemos obtener la derivada \frac{dK}{dL} haciendo un abuso del lenguaje para despejar los diferenciales de L y K de la siguiente forma

\dfrac{dK}{dL} = -\dfrac{\frac{\partial P}{\partial L}}{\frac{\partial P}{\partial K}} \ \Longrightarrow \ -\dfrac{dK}{dL} = \dfrac{\frac{\partial P}{\partial L}}{\frac{\partial P}{\partial K}} \ \Longrightarrow \ TTS = \dfrac{\frac{\partial P}{\partial L}}{\frac{\partial P}{\partial K}}

Ejemplo

Considerando una compañía que fabrica los plátano chips, ésta ha determinado que la función de producción es P(L,K)=\sqrt{L \cdot K}, donde L es el número de horas de trabajo por semana y K es el capital (expresado en miles de Perolitos por semana) requerido para la producción semanal de P gruesas de plátano chips (Una gruesa es una cantidad de artículos equivalente a doce docenas, es decir, 144 artículos.). Determine la Tasa Técnica de Sustitución.

Nota: Perolitos (Ps.) es la moneda oficial de totumat.

Debemos calcular ambas funciones de producción marginal, previamente, debemos notar que P(L,K)=\sqrt{L\cdot K} = (L \cdot K)^{\frac{1}{2}} = L^{\frac{1}{2}} \cdot k^{\frac{1}{2}}, por lo tanto

\dfrac{\partial P}{\partial L} = \frac{1}{2} \cdot L^{-\frac{1}{2}} \cdot K^{\frac{1}{2}} = \frac{1}{2} \cdot \frac{K^{\frac{1}{2}}}{L^{\frac{1}{2}}} = \frac{1}{2} \cdot \frac{\sqrt{K}}{\sqrt{L}}

\dfrac{\partial P}{\partial K} = \frac{1}{2} \cdot K^{-\frac{1}{2}} \cdot L^{\frac{1}{2}} = \frac{1}{2} \cdot \frac{L^{\frac{1}{2}}}{K^{\frac{1}{2}}} = \frac{1}{2} \cdot \frac{\sqrt{L}}{\sqrt{K}}

Luego,

TTS = \dfrac{\frac{\partial P}{\partial L}}{\frac{\partial P}{\partial K}} = \frac{\frac{1}{2} \cdot \frac{\sqrt{K}}{\sqrt{L}}}{\frac{1}{2} \cdot \frac{\sqrt{L}}{\sqrt{K}}} = \frac{K}{L}

Curvas de Nivel

Anthonny Arias-García2 comentarios

Hemos visto de forma muy superficial uno de los métodos para graficar funciones en varias variables, otro de los métodos para entender el comportamiento gráfico de este tipo de funciones es conocido como las curvas de nivel y se basa en el método que usan los cartógrafos para diseñar mapas de la superficie terrestre (y de otros cuerpos celestes). Este método consiste en dibujar los contornos que unen los puntos del mapa que representan las posiciones del terreno con la misma altitud sobre el nivel del mar, por ejemplo, el contorno de todos los puntos que se encuentran a 100 metros por encima del nivel del mar. Cuando estas curvas están muy juntas, esto indica que las pendientes están muy pronunciadas.

Veamos en la siguiente imagen tomada del mapa del relieve del Monte Everest que provee Google Maps, en las regiones donde las pendientes son menos empinadas es notorio que las curvas de nivel están bastante separadas en comparación con los alrededores de la cima del Monte Everest.

Recordemos que al definir las derivadas parciales, fijamos los valores de las variables x y y para generar curvas en planos paralelos a los planos YZ y XZ respectivamente. De esta forma, podemos representar geométricamente en una función fijando valores para la variable z para generar curvas en planos paralelos al plano XY.

Formalmente, si fijamos la variable z en un valor c, entonces la curva de nivel en c estará expresada de la forma z = f(x,y) = c.

Particularmente podemos cortar la gráfica de la función f(x,y) = x^2 + y^2 con el plano generado en z = 1 e incluso podemos estudiar sus curvas de nivel en distintos valores de z, por ejemplo, los valores enteros z=2,3,4,5,6 \ldots de la siguiente forma

Notando que a medida que crece el valor fijo de z las circunferencias están mas juntas, esto indica que a medida cada vez las pendientes están más pronunciadas y ya hemos comprobado que es así al calcular las derivadas parciales de estas funciones.

Referencias

Sydsaeter, K., & Hammond, P. J. (1998). Matemáticas para el Análisis Económico (1st ed.; A. Otero, ed.). Prentice Hall.