Al sumar números reales tenemos la libertad de asociar los números involucrados con ligereza y de igual forma, podemos asociar los números involucrados si estamos multiplicando números reales, sin embargo, debemos ser precavidos cuando nos topamos con operaciones mixtas, es decir, sumas y productos al mismo tiempo. A continuación veremos una propiedad que nos permite operar sumas y productos al mismo tiempo.
También pudiera interesarte
La propiedad distributiva establece que si un número multiplica a la suma de dos números, entonces el factor involucrado se distribuye entre cada uno de los sumandos. Formalmente, si ,
y
son números reales, entonces

Podemos también aplicar esta propiedad si dentro de los paréntesis está involucrada una resta en vez de una suma, de la siguiente forma:

Notamos que si observamos esta igualdad de derecha a izquierda, estamos tomando el factor común que hay en ambos sumandos y lo estamos sacando a multiplicar:
Esta es una de las propiedades más usadas en al cálculo de operaciones mixtas y a partir de ellas, se deducen algunos casos que facilitan la simplificación de expresiones matemáticas. Veamos algunos ejemplos para entender bien esta propiedad:
Ejemplos
Ejemplo 1
Use la propiedad distributiva para expandir la expresión . En este caso no es necesario usar la propiedad distributiva ya que podemos sumar los números que están dentro de los paréntesis y posteriormente multiplicar de la siguiente forma:
Ejemplo 2
Use la propiedad distributiva para expandir la expresión . Notemos que uno de los sumandos involucrados es la raíz cuadrada de 6, por lo tanto no se puede sumar con 1, entonces distribuimos el factor involucrado
Ejemplo 3
Use la propiedad distributiva para expandir la expresión . Notemos que uno de los sumandos involucrados es la raíz cuadrada de 10 y el otro es una incógnita, por lo tanto no se pueden restar, entonces distribuimos el factor involucrado
Ejemplo 4
Use la propiedad distributiva para expandir la expresión . Notemos que uno de los sumandos involucrados una incógnita y el otro es una incógnita elevada al cuadrado, por lo tanto no se pueden sumar, entonces distribuimos el factor involucrado
Ejemplo 5
Use la propiedad distributiva para sacar el factor común de la expresión . Notemos que
, entonces,
Ejemplo 6
Use la propiedad distributiva para sacar el factor común de la expresión . Notemos que uno de los sumandos involucrados es una incógnita elevada a la cuatro y el otro es 8 veces dicha incógnita, por lo tanto no se pueden restar, entonces
Ejemplo 7
Use la propiedad distributiva para sacar el factor común de la expresión . Estos dos elementos no se pueden sumar, entonces
Ejemplo 8
Use la propiedad distributiva para expandir la expresión . Notemos que podemos agrupar los elementos que están dentro de los paréntesis, para obtener
Sumamos los elementos que están multiplicando a y por otra parte, los términos independientes.
Finalmente, efectuamos la propiedad distributiva.
Ejemplo 9
Use la propiedad distributiva para expandir la expresión . Notemos que podemos agrupar los elementos que están dentro de los paréntesis, para obtener
Sumamos los elementos que están multiplicando a , por otra parte los elementos que están multiplicando a
y por otra parte, los términos independientes.
Finalmente, efectuamos la propiedad distributiva.
Ejemplo 10
Use la propiedad distributiva para expandir la expresión . Pese a que la variable
aparece como un factor en el lado derecho de la expresión, podemos distribuirlo en cada uno de los sumandos tal como si apareciera del lado izquierdo:
Notando que al multiplicar $q \cdot q$, ambos factores tienen la misma base, entonces obtenemos lo siguiente

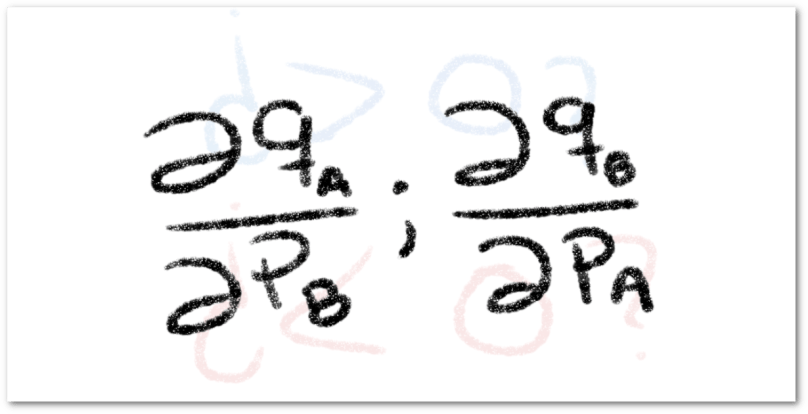
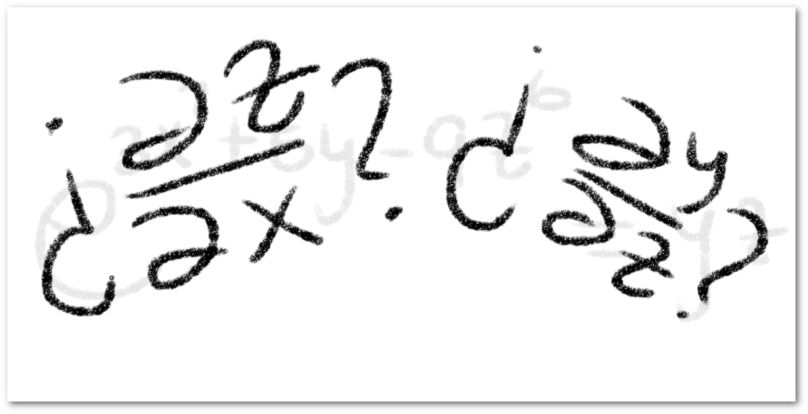





Debe estar conectado para enviar un comentario.