- Definición de Sucesión
- Ejemplos
- Ejemplo 1: Sucesión Constante
- Ejemplo 2: Sucesión de los Números Naturales
- Ejemplo 3: Sucesión de Proporcionalidad Inversa
- Ejemplo 4
- Ejemplo 5: Sucesión de los Números Pares
- Ejemplo 6: Sucesión de los Números Impares
- Ejemplo 7: Sucesión Alternante
- Ejemplo 8: Sucesión Recursiva
A menudo, en las matemáticas, es necesario proceder paso a paso, contando detalladamente lo que ocurre en cada paso. Es por esto que definimos las sucesiones, pues tomando en cuenta que el conjunto de los números naturales es un conjunto contable, podemos establecer una relación entre estos y cualquier conjunto para estudiar su comportamiento.
Las sucesiones sientan una base para el cálculo infinitesimal y además, permiten, estudiar fenómenos en distintos ámbitos de las ciencias básicas y ciencias sociales.
También pudiera interesarte
Definición de Sucesión
Definimos una sucesión de números reales como una regla de correspondencia que corresponde a cada número natural con un único número real, es decir, una sucesión es una función que parte de desde 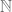 y llega hasta
y llega hasta 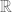 , entonces, si
, entonces, si  es una sucesión, tenemos que:
es una sucesión, tenemos que:
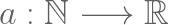
Al trabajar con sucesiones, la notación de función puede sobrecargar la nomenclatura, es por esto que la regla de correspondencia  para cada
para cada 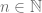 que define la sucesión usualmente se denota de la siguiente forma
que define la sucesión usualmente se denota de la siguiente forma

De esta forma, podemos expresar a las sucesiones como conjuntos, ya sea de forma comprensiva, definiendo la regla general que define a todos los elementos del conjunto o de forma extensiva, nombrando todos sus elementos como veremos a continuación:
Aunque también se puede expresar de forma comprensiva usando las notaciones  o
o  .
.
Al ser las sucesiones representadas como conjuntos, llamaremos elemento a cada número real que la compone, sin embargo, para ser más específicos, al hacer referencia a la posición que cada elemento en el orden de la sucesión, se le llamará término.
Veamos en los siguientes ejemplos algunas de las sucesiones básicas. Como ejercicio mental para el lector, vea primero el conjunto que define la sucesión y piense cual es la regla general que la define.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 1: Sucesión Constante
Si consideramos la sucesión  , notamos que esta sucesión se genera correspondiendo a cada número natural con el número
, notamos que esta sucesión se genera correspondiendo a cada número natural con el número 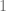 . De forma que
. De forma que
Esta sucesión será llamada sucesión constante uno y la regla general que define a esta sucesión es
 .
.
De forma general, la sucesión  definida por
definida por 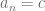 donde
donde  es un número real, será llamada sucesión constante
es un número real, será llamada sucesión constante  .
.
Ejemplo 2: Sucesión de los Números Naturales
Si consideramos la sucesión 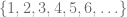 , notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo. De forma que
, notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo. De forma que
Esta sucesión será llamada sucesión de los números naturales y la regla general que define a esta sucesión es
 .
.
Ejemplo 3: Sucesión de Proporcionalidad Inversa
Si consideramos la sucesión  , notamos que esta sucesión se genera correspondiendo a cada número natural con el número
, notamos que esta sucesión se genera correspondiendo a cada número natural con el número 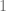 dividido el número natural correspondiente. De forma que
dividido el número natural correspondiente. De forma que
Esta sucesión será llamada sucesión de proporcionalidad inversa y la regla general que define a esta sucesión es
 .
.
Ejemplo 4
Si consideramos la sucesión  , notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo dividido entre el número natural siguiente. De forma que
, notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo dividido entre el número natural siguiente. De forma que
La regla general que define a esta sucesión es
 .
.
Ejemplo 5: Sucesión de los Números Pares
Si consideramos la sucesión  , notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo, multiplicado por dos. De forma que
, notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo, multiplicado por dos. De forma que
Esta sucesión será llamada sucesión de los números pares y la regla general que define a esta sucesión es
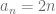
Ejemplo 6: Sucesión de los Números Impares
Si consideramos la sucesión  , notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo, multiplicado por dos menos uno, es decir, restando uno a cada número par. De forma que
, notamos que esta sucesión se genera correspondiendo a cada número natural con él mismo, multiplicado por dos menos uno, es decir, restando uno a cada número par. De forma que
Esta sucesión será llamada sucesión de los números impares y la regla general que define a esta sucesión es

Ejemplo 7: Sucesión Alternante
Si consideramos la sucesión  , notamos que esta sucesión se genera correspondiendo a cada número natural con el número
, notamos que esta sucesión se genera correspondiendo a cada número natural con el número 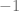 multiplicado por sí mismo la cantidad de veces correspondiente a dicho número natural. De forma que
multiplicado por sí mismo la cantidad de veces correspondiente a dicho número natural. De forma que
Esta sucesión será llamada sucesión alternante y la regla general que define a esta sucesión es

Ejemplo 8: Sucesión Recursiva
Si consideramos la sucesión 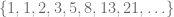 , notamos que esta sucesión se genera definiendo los dos primeros elementos, y de ahí en adelante, sumamos los dos elementos anteriores. De forma que
, notamos que esta sucesión se genera definiendo los dos primeros elementos, y de ahí en adelante, sumamos los dos elementos anteriores. De forma que
Esta sucesión es conocida como la Sucesión de Fibonacci y la regla general que define a esta sucesión es
 .
.
De forma general, todas aquellas sucesiones tales que su n-ésimo término es define a partir de términos anteriores, son conocidas como sucesiones recursivas.
es creciente si a medida que crece el valor de
, entonces crece su valor correspondiente. Formalmente, si
para todo par de números naturales
, y más aún, diremos que
es estrictamente creciente si
para todo par de números naturales
. Una forma de ver el comportamiento de una sucesión es observando su gráfica en el plano cartesiano, veamos algunos ejemplos de este tipo de sucesiones:
, esta sucesión es creciente, más aún, es estrictamente creciente.
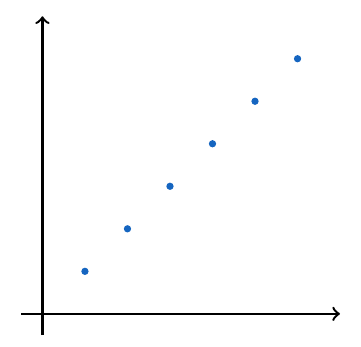
, esta sucesión es creciente, más aún, es estrictamente creciente.
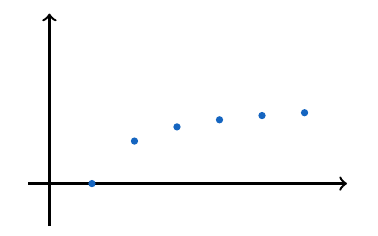
, esta sucesión es creciente, sin embargo, no es estrictamente creciente.
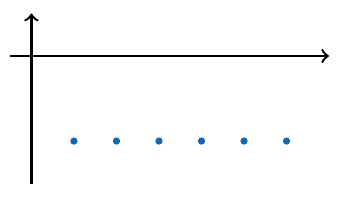
es \textbf{decreciente} si a medida que crece el valor de
, entonces decrece su valor correspondiente. Formalmente, si
para todo par de números naturales
, y más aún, diremos que
es estrictamente creciente si
para todo par de números naturales
. Una forma de ver el comportamiento de una sucesión es observando su gráfica en el plano cartesiano, veamos algunos ejemplos de este tipo de sucesiones:
, esta sucesión es decreciente, más aún, es estrictamente decreciente.

, esta sucesión es decreciente, más aún, es estrictamente decreciente.
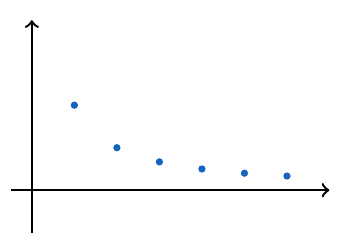
, esta sucesión es creciente, sin embargo, no es estrictamente creciente.
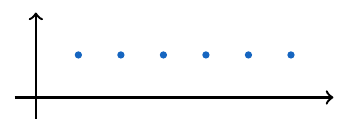
y veamos su comportamiento de forma gráfica:



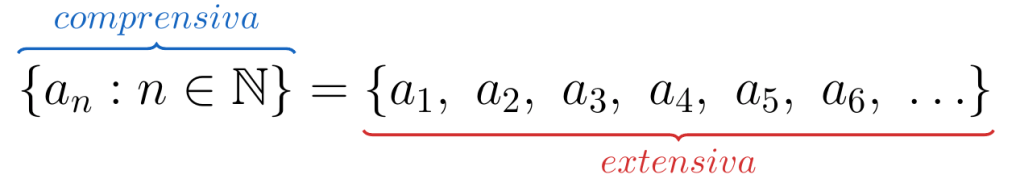
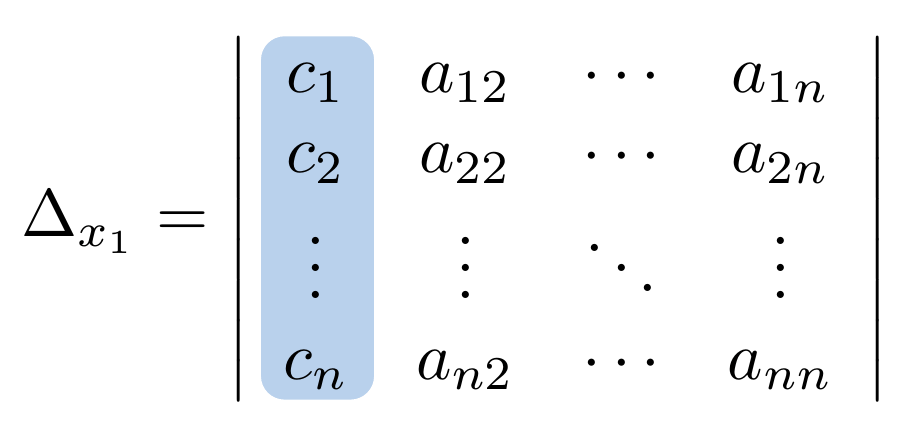
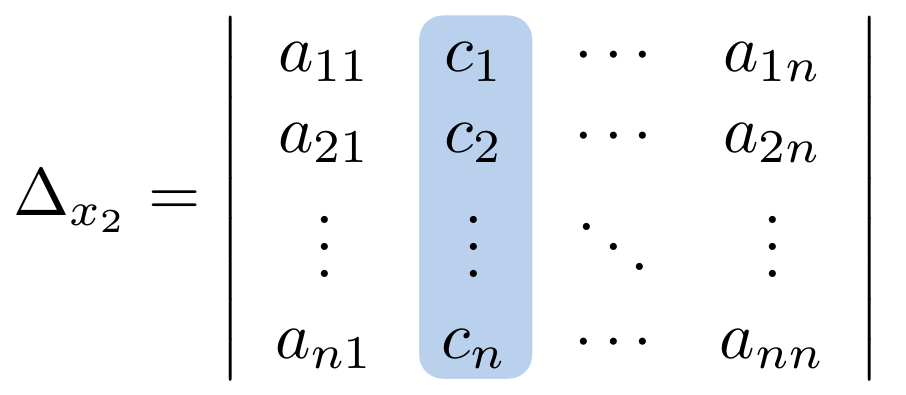
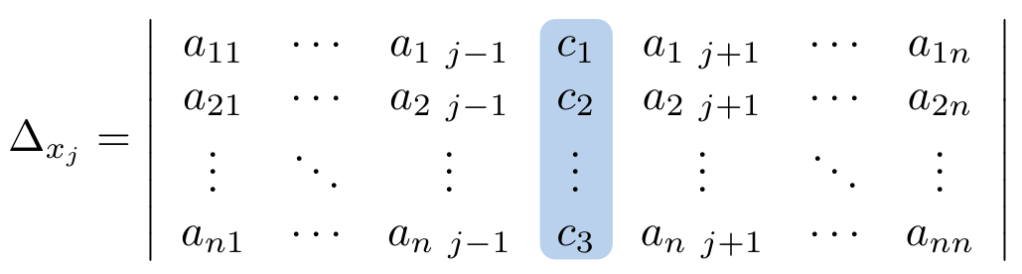
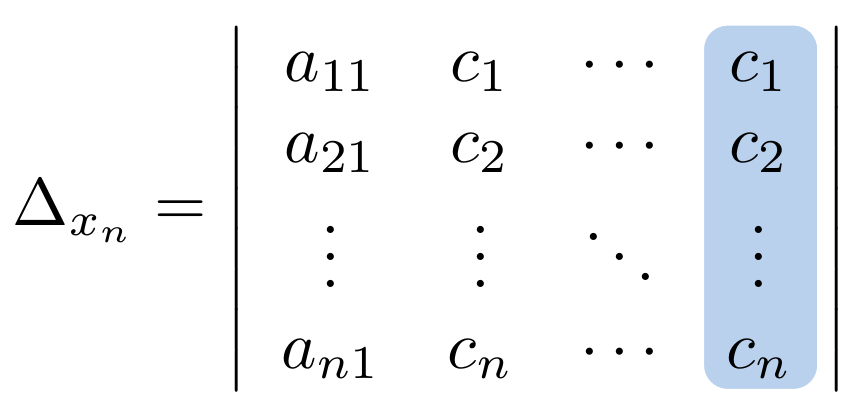
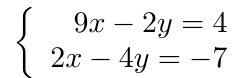
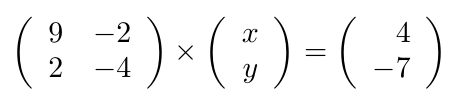
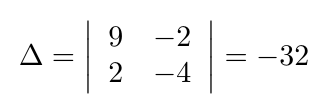
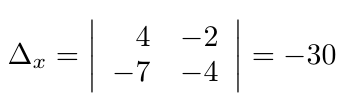

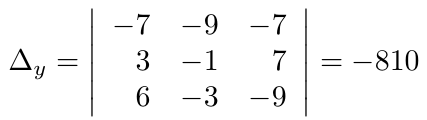
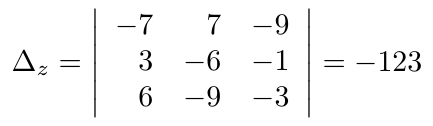

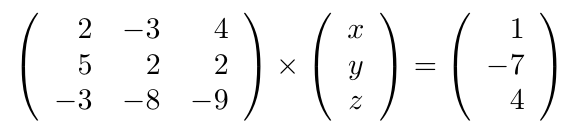
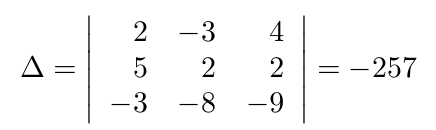
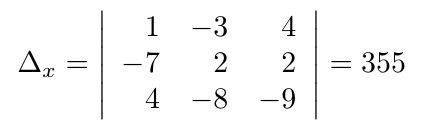
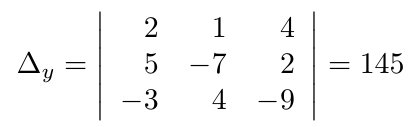
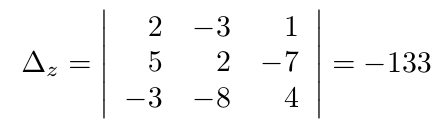
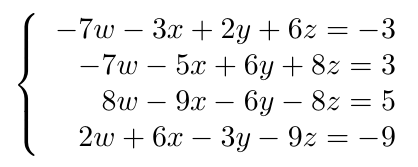



















Debe estar conectado para enviar un comentario.