Las ecuaciones diferenciales ordinarias de variables separables representan sólo una pequeña porción en el universo de las ecuaciones diferenciales, es por esto que debemos generalizar nuestras definiciones paso a paso para poder abordar ecuaciones diferenciales menos triviales.
También pudiera interesarte
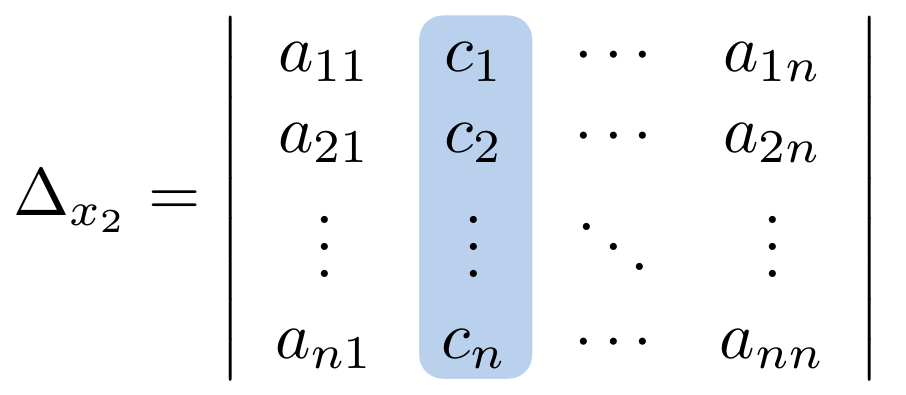
Definición
Entonces, definimos las Ecuaciones Diferenciales Ordinarias Lineales como aquellas que se expresan de la siguiente forma
Diremos que una ecuación diferencial ordinaria lineal es homogénea si , por otra parte, diremos que es no-homogénea si
. Podemos notar que toda ecuación diferencial ordinaria lineal homogénea es de variables separables pues
Sabiendo esto, en esta sección descartaremos las ecuaciones diferenciales ordinarias lineales homogéneas y nos enfocaremos en el caso en que éstas sean no-homogéneas.
Antes de explicar el procedimiento para calcular la solución de este tipo de ecuaciones, debemos tener claros algunos elementos: Diremos que una ecuación diferencial ordinaria lineal está expresada en su forma estándar si el coeficiente que multiplica a la derivada de mayor orden involucrada en la ecuación es exactamente igual a uno, es decir, que está expresada de la siguiente forma
Y decimos que estandarizar una ecuación diferencial ordinaria lineal es reescribirla en su forma estándar.
El Factor Integrante
El procedimiento que usaremos para calcular la solución de las ecuaciones diferenciales ordinarias lineales no-homogéneas se basa en encontrar factor tal que al multiplicarlo por cada sumando de la ecuación, ésta se reduce a una ecuación homogénea. A este factor lo llamaremos factor integrante y lo definimos como
Veamos con algunos ejemplos como calcular la solución de este tipo de ecuaciones diferenciales.
Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.
Ejemplos
Ejemplo 1
Calcule la solución de la siguiente ecuación diferencial ordinaria lineal no-homogénea:
Lo primero que debemos notar es que esta ecuación no está expresada en su forma estándar así que aún no podemos identificar la función para definir nuestro factor integrante, para estandarizarla debemos dividir cada uno de sus sumandos por 5 para obtener
Una vez estandarizada, podemos concluir que , así que nuestro factor integrante es
Ahora multiplicamos cada uno de los sumandos de nuestra ecuación estandarizada por el factor integrante
Notando que la suma expresada en el lado izquierdo de la ecuación es justamente de la derivada del producto , así que podemos reescribir la ecuación de la siguiente forma:
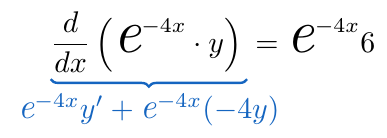
Expresados ambos elementos de la ecuación de esta forma, calculamos la integral de ambas expresiones respecto a la variable tal como se ha planteado al calcular la solución de ecuaciones diferenciales de variables separables.
Finalmente, despejamos para obtener la solución general de la ecuación diferencial.
Ejemplo 2
Calcule la solución de la siguiente ecuación diferencial ordinaria lineal no-homogénea:
Lo primero que debemos notar es que esta ecuación no está expresada en su forma estándar así que aún no podemos identificar la función para definir nuestro factor integrante, para estandarizarla debemos dividir cada uno de sus sumandos por
para obtener
Una vez estandarizada, podemos concluir que , así que nuestro factor integrante es
Ahora multiplicamos cada uno de los sumandos de nuestra ecuación estandarizada por el factor integrante
Cuyos sumandos podemos simplificar de la siguiente forma:
Notando que la suma expresada en el lado izquierdo de la ecuación es justamente de la derivada del producto , así que podemos reescribir la ecuación de la siguiente forma:
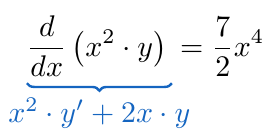
Expresados ambos elementos de la ecuación de esta forma, calculamos la integral de ambas expresiones respecto a la variable tal como se ha planteado al calcular la solución de ecuaciones diferenciales de variables separables.
Finalmente, despejamos para obtener la solución general de la ecuación diferencial.
Ejemplo 3
Calcule la solución de la siguiente ecuación diferencial ordinaria lineal no-homogénea con el problema de valor inicial indicado:
Lo primero que debemos notar es que esta ecuación no está expresada en su forma estándar así que aún no podemos identificar la función para definir nuestro factor integrante, para estandarizarla debemos dividir cada uno de sus sumandos por
para obtener
Una vez estandarizada, podemos concluir que , así que nuestro factor integrante es
Ahora multiplicamos cada uno de los sumandos de nuestra ecuación estandarizada por el factor integrante
Cuyos sumandos podemos simplificar de la siguiente forma:
Notando que la suma expresada en el lado izquierdo de la ecuación es justamente de la derivada del producto , así que podemos reescribir la ecuación de la siguiente forma:
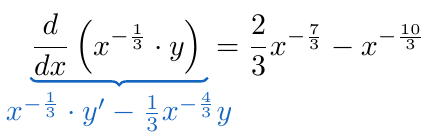
Expresados ambos elementos de la ecuación de esta forma, calculamos la integral de ambas expresiones respecto a la variable tal como se ha planteado al calcular la solución de ecuaciones diferenciales de variables separables.
Finalmente, despejamos para obtener la solución general de la ecuación diferencial.
Una vez que hemos calculado la solución general de esta ecuación diferencial, debemos encontrar la solución particular que cumple con el problema de valor inicial. Para esto, sustituimos los valores y
en la solución general para posteriormente despejar
De esta forma, concluimos que la solución que satisface el problema de valor inicial es
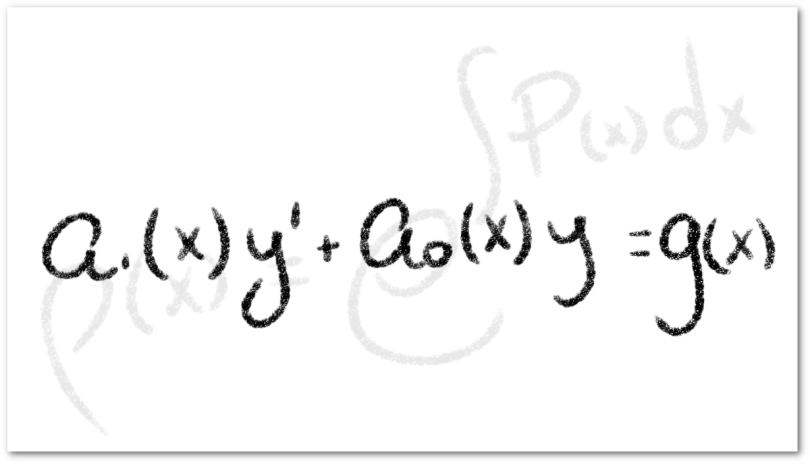
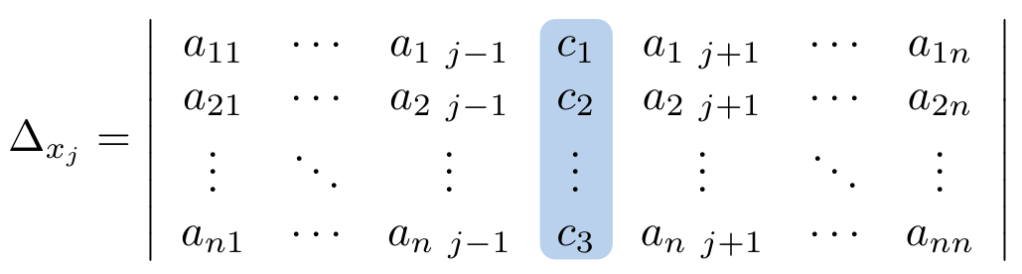
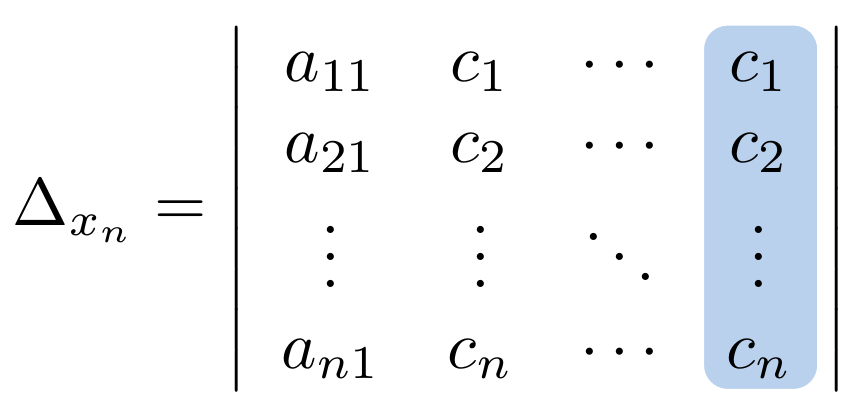
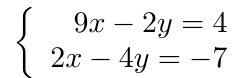
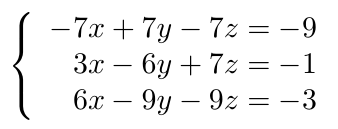

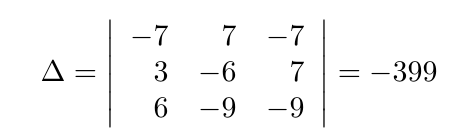
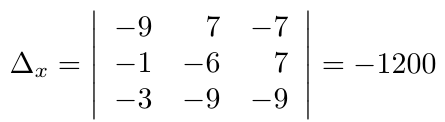
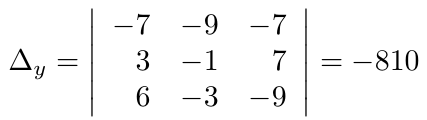
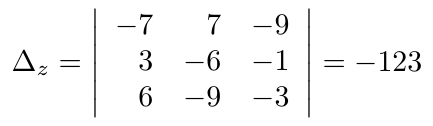

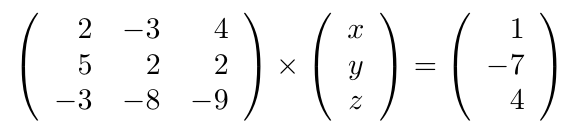
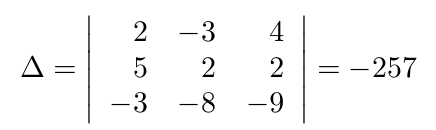
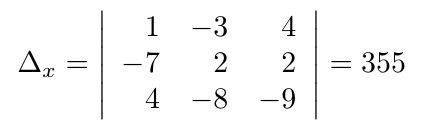
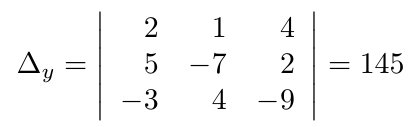
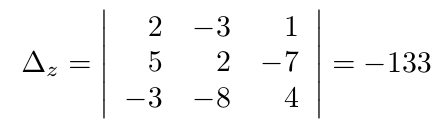
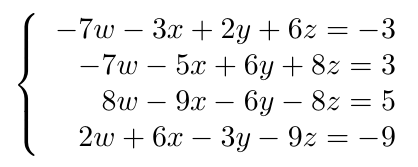
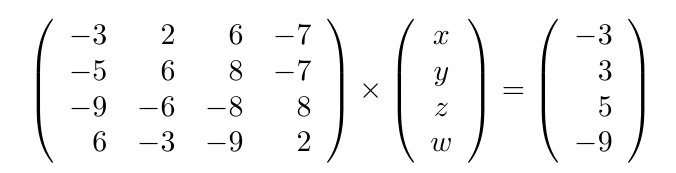
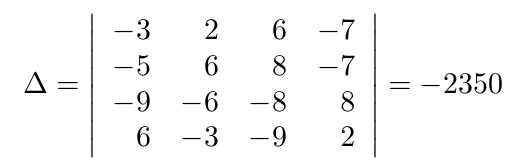
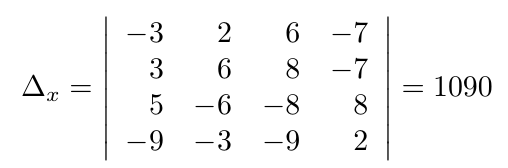
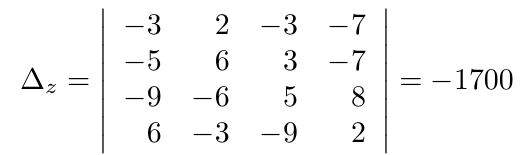
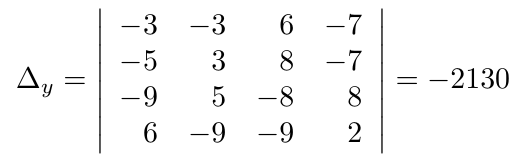






Debe estar conectado para enviar un comentario.