Etiqueta: Ecuaciones Homogéneas

Ejercicios Propuestos - Ecuaciones Diferenciales

Ejercicios Propuestos – Ecuaciones Diferenciales Ordinarias lineales homogéneas con coeficientes constantes

Anthonny Arias-GarcíaDeja un comentario

Calcule la solución de las siguientes Ecuaciones Diferenciales Ordinarias lineales homogéneas de segundo orden determinando la ecuación auxiliar.

  1. 10 y'' + 50 y'+ 60y = 0
  2. y'' + 5 y'+ 6y = 0
  3. 2 y'' - 12 y'+ 10y = 0
  4. - 5 y'' - 45 y'- 100y = 0
  1. 4 y''' - 12 y'' + 12 y'- 4y = 0
  2. 3 y''' + 12 y'' = 0
  3. 9 y''' + 108 y'' + 405 y'+ 450y = 0
  4. 5 y''' + 15 y'' - 5 y'- 15y = 0
  1. - 6 y^{(4)} + 6 y''' + 84 y'' - 144 y' = 0
  2. 3 y^{(4)} + 21 y''' + 18 y'' - 96 y'- 96y = 0
  3. - 3 y^{(4)} - 6 y''' + 9 y'' + 24 y'+ 12y = 0
  4. 5 y^{(4)} - 10 y''' - 15 y'' + 40 y'- 20y = 0
  1. 2 y^{(5)} + 8 y^{(4)} - 44 y''' - 200 y'' - 150 y' = 0
  2. 5 y^{(5)} - 145 y''' + 500 y' = 0
  3. 2 y^{(5)} - 6 y^{(4)} - 50 y''' + 166 y'' + 48 y'- 160y = 0
  4. - 10 y^{(5)} - 40 y^{(4)} + 130 y''' + 520 y'' - 360 y'- 1440y = 0

También pudiera interesarte

Ejercicios Propuestos - Ecuaciones Diferenciales

Ejercicios Propuestos – Ecuaciones Diferenciales Ordinarias Lineales Homogéneas con una solución conocida

Anthonny Arias-GarcíaDeja un comentario

Calcule la solución de las siguientes Ecuaciones Diferenciales Ordinarias de segundo orden tomando en cuenta la solución particular y_1 indicada.

  1. 8 x^{2} y'' + 4 x y' - 24 y = 0 con solución particular y_1 = - 9 x^{2}
  2. 10 x^{2} y'' - 20 y = 0 con solución particular y_1 = - 5 x^{2}
  3. - 9 x^{2} y'' + 6 x y' + 6 y = 0 con solución particular y_1 = - 7 x^{2}
  4. - 2 x^{2} y'' + 7 x y' - 10 y = 0 con solución particular y_1 = 2 x^{2}
  1. 5 x^{2} y'' + 3 x y' - 16 y = 0 con solución particular y_1 = 5 x^{2}
  2. - 3 x^{2} y'' + 3 x y' = 0 con solución particular y_1 = 6 x^{2}
  3. 4 x^{2} y'' - 4 x y' = 0 con solución particular y_1 = - 5 x^{2}
  4. 2 x^{2} y'' - 2 x y' = 0 con solución particular y_1 = - 6 x^{2}
  1. - 126 y - 2 y' + y'' = 0 con solución particular y_1 = - \textit{\Large e}^{9 x}
  2. - 280 y + y' + 9 y'' = 0 con solución particular y_1 = 4 \textit{\Large e}^{- 4 x}
  3. - 800 y - 2 y' + 6 y'' = 0 con solución particular y_1 = 7 \textit{\Large e}^{- 8 x}
  4. 20 y - 9 y' - 7 y'' = 0 con solución particular y_1 = 5 \textit{\Large e}^{- 2 x}
  1. - 8 y' + 4 y'' = 0 con solución particular y_1 = 6 \textit{\Large e}^{2 x}
  2. - 36 y + 9 y' + 9 y'' = 0 con solución particular y_1 = 7 \textit{\Large e}^{- 2 x}
  3. - 2 y - 9 y' - 8 y'' = 0 con solución particular y_1 = 5 \textit{\Large e}^{- x}
  4. 72 y - 6 y' - 6 y'' = 0 con solución particular y_1 = - 4 \textit{\Large e}^{- 3 x}

También pudiera interesarte

Ejercicios Propuestos - Ecuaciones Diferenciales

Ejercicios Propuestos – Ecuaciones Homogéneas de grado alpha ⍺

Anthonny Arias-GarcíaDeja un comentario

Una ecuación de la forma

M(x,y)dx + N(x,y)dy = 0

es homogénea si M(x,y) y N(x,y) son funciones homogéneas del mismo grado, es decir,

M(tx,ty) = t^\alpha M(x,y) \text{ y } N(tx,ty) = t^\alpha N(x,y), \, \alpha \in \mathbb{R}

En este caso, las sustituciones y=ux o x=vy reducen la ecuación diferencial homogénea de grado \alpha a una Ecuación Diferencial de Variables Separables.

Halle la función y que satisface las siguientes ecuaciones diferenciales. Halle además, la función que satisface el valor inicial donde corresponda.

  1. \left(- 65 x^{3} y^{2} + x^{2} y^{3}\right) dx + \left(210 x^{5} + 4 x^{3} y^{2}\right) dy = 0
  2. \left(5 x^{2} y^{4} - 24 y^{6}\right) dx + \left(- 3 x^{3} y^{3} + 2 x^{2} y^{4}\right) dy = 0
  3. \left(4 x^{2} y^{3} - 18 y^{5}\right) dx + \left(- 5 x^{3} y^{2} + 9 x^{2} y^{3}\right) dy = 0
  4. \left(- 6 x^{8} y^{2} - 15 x^{7} y^{3}\right) dx + \left(36 x^{10} + 9 x^{8} y^{2}\right) dy = 0
  1. \left(5 x^{2} y^{4} + 8 y^{6}\right) dx + \left(- x^{3} y^{3} - 12 x^{2} y^{4}\right) dy = 0
  2. \left(40 x^{5} y^{2} - 14 x^{4} y^{3}\right) dx + \left(- 48 x^{7} + 6 x^{5} y^{2}\right) dy = 0
  3. \left(9 x^{2} y^{8} - 84 y^{10}\right) dx + \left(- 15 x^{3} y^{7} + 54 x^{2} y^{8}\right) dy = 0
  4. \left(80 x^{6} y^{2} + x^{5} y^{3}\right) dx + \left(168 x^{8} + 7 x^{6} y^{2}\right) dy = 0
  1. \left(6 x^{2} y^{5} - 72 y^{7}\right) dx + \left(- 2 x^{3} y^{4} - 28 x^{2} y^{5}\right) dy = 0
  2. \left(- 8 x^{4} y^{2} - 6 x^{3} y^{3}\right) dx + \left(- 16 x^{6} + 5 x^{4} y^{2}\right) dy = 0
  3. \left(9 x^{2} y^{8} + 48 y^{10}\right) dx + \left(- 15 x^{3} y^{7} - 42 x^{2} y^{8}\right) dy = 0
  4. \left(2 x^{7} y^{2} - 9 x^{6} y^{3}\right) dx + \left(24 x^{9} + 8 x^{7} y^{2}\right) dy = 0
  1. \left(4 x^{2} y^{3} + 81 y^{5}\right) dx + \left(- 7 x^{3} y^{2} + 18 x^{2} y^{3}\right) dy = 0
  2. \left(52 x^{7} y^{2} - 4 x^{6} y^{3}\right) dx + \left(144 x^{9} + 8 x^{7} y^{2}\right) dy = 0
  3. \left(9 x^{2} y^{8} - 36 y^{10}\right) dx + \left(- 18 x^{3} y^{7} - 45 x^{2} y^{8}\right) dy = 0
  4. \left(77 x^{8} y^{2} - 16 x^{7} y^{3}\right) dx + \left(- 168 x^{10} + 9 x^{8} y^{2}\right) dy = 0
  1. \left(51 x y^{7} - 3 y^{8}\right) dx + \left(324 x^{4} y^{4} - 252 x^{3} y^{5}\right) dy = 0
  2. \left(- 46 x y^{3} + 70 y^{4}\right) dx + \left(- 2 x^{4} - 22 x^{3} y\right) dy = 0
  3. \left(- 120 x^{6} y^{3} - 6 x^{5} y^{4}\right) dx + \left(- 1296 x^{9} - 738 x^{8} y\right) dy = 0
  4. \left(531 y^{5} - \frac{630 y^{6}}{x}\right) dx + \left(9 x^{3} y^{2} - 126 x^{2} y^{3}\right) dy = 0
  1. \left(4 x^{6} y^{2} - 2 x^{5} y^{3}\right) dx + \left(- \frac{120 x^{9}}{y} + 46 x^{8}\right) dy = 0
  2. \left(27 y^{4} - \frac{54 y^{5}}{x}\right) dx + \left(3 x^{3} y + 24 x^{2} y^{2}\right) dy = 0
  3. \left(55 x^{6} y^{2} - 5 x^{5} y^{3}\right) dx + \left(\frac{80 x^{9}}{y} - 130 x^{8}\right) dy = 0
  4. \left(- 795 y^{5} + \frac{1890 y^{6}}{x}\right) dx + \left(- 5 x^{3} y^{2} + 110 x^{2} y^{3}\right) dy = 0

También pudiera interesarte

Ecuaciones Diferenciales Ordinarias lineales con coeficientes constantes (Homogéneas)

Anthonny Arias-GarcíaDeja un comentario
  1. Ecuaciones Diferenciales Ordinarias lineales homogéneas con coeficientes constantes de segundo orden
  2. La Ecuación Auxiliar
    1. Discriminante positivo
    2. Discriminante igual a cero
    3. Discriminante negativo
    4. Ejemplos
      1. Ejemplo 1
      2. Ejemplo 2
      3. Ejemplo 3
  3. Ecuaciones Diferenciales Ordinarias lineales homogéneas con coeficientes constantes de n-ésimo orden
    1. Ejemplos
      1. Ejemplo 4
      2. Ejemplo 5

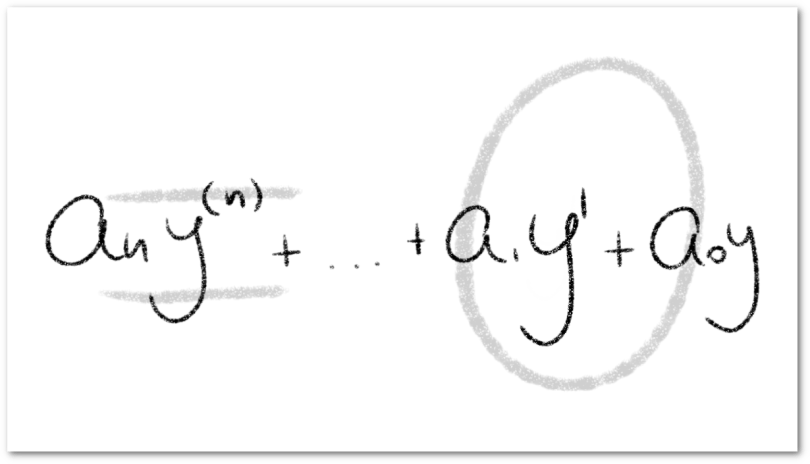
Los métodos para calcular al solución ecuaciones diferenciales ordinarias de orden superior dependen de la forma en que la ecuación esté expresada, considerando el caso lineal, es posible particularizarlo aún más, pues si consideremos una ecuación diferencial de la forma

a_n(x) y^{(n)} + \ldots + a_1(x) y' + a_0(x) y = g(x)

Las funciones a_0(x), a_1(x), \ldots, a_n(x) que definen los coeficientes de la ecuación, pueden considerarse como funciones constantes, de forma que la ecuación diferencial queda expresada como

a_n y^{(n)} + \ldots + a_1 y' + a_0 y = g(x)

Donde a_0, a_1, \ldots, a_n son números reales.

Más aún, será de vital importancia clasificar estas ecuaciones dependiendo del valor de g(x). Diremos que una ecuación de este tipo es homogénea si g(x)=0, y durante esta sección, este es el caso que desarrollaremos.

También pudiera interesarte

Ecuaciones Diferenciales Ordinarias lineales homogéneas con coeficientes constantes de segundo orden

Consideremos de forma particular, una ecuación diferencial ordinaria lineal con coeficientes constantes de segundo orden, de la cual no conocemos ninguna solución particular, expresada de la siguiente forma:

ay'' + by' + cy = 0

Notemos que al ser todos sus coeficientes constantes, entonces todos sus coeficientes son funciones continuas en cualquier intervalo I, por lo tanto podemos garantizar que existe una solución.

La Ecuación Auxiliar

La ecuación que hemos considerado se puede reescribir como y'' = \alpha y' + \beta y, esta expresión sugiere que la segunda derivada de la solución que estamos buscando es una combinación lineal de la primera y segunda derivada. Podemos intuir con certeza que una función de la forma y=\textit{\Large e}^{mx} cumple con esta propiedad pues

y=\textit{\Large e}^{mx}

y'=m\textit{\Large e}^{mx}

y''=m^2\textit{\Large e}^{mx}

Entonces, sustituyendo esta función y sus derivadas en la ecuación que hemos planteado, tenemos que

am^2\textit{\Large e}^{mx} + bm\textit{\Large e}^{mx} + c\textit{\Large e}^{mx} = 0

Podemos factorizar esta expresión, pues si sacamos \textit{\Large e}^{mx} como un factor obtenemos

\textit{\Large e}^{mx} ( am^2 + bm + c) = 0

Tomando en cuenta que la función exponencial siempre es distinta de cero, tenemos que \textit{\Large e}^{mx} \neq 0, entonces para que esta igualdad se satisfaga, necesariamente el otro factor involucrado debe ser igual a cero, es decir,

am^2 + bm + c = 0

Esta última es una ecuación cuadrática y en este caso la llamamos ecuación auxiliar. Nuestro propósito será el calcular el valor m que la satisface pues de esta forma hallamos la función y, para esto usamos el método del discriminante del cual obtenemos dos valores.

m_1 = \frac{-b + \sqrt{b^2-4ac}}{2a} \text{ y } m_2 = \frac{-b - \sqrt{b^2-4ac}}{2a}

A partir de aquí debemos tener tres consideraciones antes de que expresar nuestra solución:

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Discriminante positivo

Si b^2-4ac > 0, entonces m_1 y m_2 son dos números reales distintos, obtenemos dos soluciones particulares y_1 = \textit{\Large e}^{m_1 x} y y_2 = \textit{\Large e}^{m_2 x} por lo que la solución general está definida como

y = c_1 \textit{\Large e}^{m_1 x} + c_2 \textit{\Large e}^{m_2 x}

Discriminante igual a cero

Si b^2-4ac = 0, entonces m_1 y m_2 son dos números reales exactamente iguales \frac{-b}{2a}, por lo que la una solución particular está definida como y_1=\textit{\Large e}^{m_1x}, sin embargo, ¿cómo determinamos la otra solución particular?

Considerando la ecuación ay'' + by' + cy = 0, entonces estandarizamos la ecuación

y'' + \frac{b}{a}y' + \frac{c}{a}y = 0

Y recordemos que si conocemos una solución particular y_1 de una ecuación, la otra solución particular y_2 se puede calcular aplicando la siguiente fórmula

y_2(x) \ = \ y_1(x) \int \frac{\textit{\Huge e}^{\tiny - \int P dx}}{ \left( y_1(x) \right)^2} dx

= \ \textit{\Large e}^{m_1 x} \int \frac{\textit{\Huge e}^{\tiny - \int \frac{b}{a} dx}}{ \left( \textit{\Large e}^{m_1 x} \right)^2} dx

= \ \textit{\Large e}^{m_1 x} \int \frac{\textit{\Huge e}^{\tiny - \int \frac{b}{a} dx}}{ \left( \textit{\Large e}^{\frac{-b}{2a} x} \right)^2} dx

= \ \textit{\Large e}^{m_1 x} \int \frac{\textit{\Large e}^{\tiny - \frac{b}{a} x}}{ \textit{\Large e}^{- \frac{b}{a} x} } dx

= \ \textit{\Large e}^{m_1 x} \int dx

= \ x \textit{\Large e}^{m_1 x}

Por lo tanto, la solución general está definida como

y = c_1 \textit{\Large e}^{m_1x} + c_2 x \textit{\Large e}^{m_1x}

Discriminante negativo

Si b^2-4ac < 0, entonces m_1 y m_2 son dos números complejos distintos de la forma m_1=\alpha + i\beta y m_2=\alpha-i\beta donde \alpha,\beta<0 e i^2=-1. Formalmente no hay diferencia entre este y el primer caso, por lo que la solución será

y = c_1 \textit{\Large e}^{(\alpha + i\beta)x} + c_2 \textit{\Large e}^{(\alpha + i\beta)x}

Sin embargo, será necesario reescribir esta función en términos de números reales, por esta razón recurrimos a una serie de artilugios matemáticos que al final nos darán como resultado

y = c_1 \textit{\Large e}^{\alpha x} cos(\beta x) + c_2 \textit{\Large e}^{\alpha x} sen(\beta x)

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ejemplos

Ejemplo 1

Calcule la solución de la siguiente ecuación diferencial ordinaria lineal homogénea con coeficientes constantes

2y'' - 5y' -3y = 0

Empezamos escribiendo la ecuación auxiliar correspondiente a esta ecuación diferencial

2m^2 - 5m - 3 = 0

Y aplicando el método del discriminante obtenemos que

m = \frac{-(-5) \pm \sqrt{(-5)^2-4(2)(-3)}}{2(2)}

Por lo tanto, m_1=\frac{1}{2} y m_2=3 son las raíces de este polinomio y así, la solución general es esta ecuación diferencial viene dada por

y = c_1 \textit{\Large e}^{-\frac{1}{2}x} + c_2 \textit{\Large e}^{3x}

Ejemplo 2

Calcule la solución de la siguiente ecuación diferencial ordinaria lineal homogénea con coeficientes constantes

y'' - 10y' + 25y = 0

Empezamos escribiendo la ecuación auxiliar correspondiente a esta ecuación diferencial

m^2 - 10m - 25 = 0

Y aplicando el método del discriminante obtenemos que

m = \frac{-(-10) \pm \sqrt{(-10)^2-4(1)(-25)}}{2(1)}

Por lo tanto, m_1=5 y m_2=5 son las raíces de este polinomio y notando que ambas son la misma raíz, decimos que esta tiene multiplicidad igual a 2, por lo tanto la solución general es esta ecuación diferencial viene dada por

y = c_1 \textit{\Large e}^{5x} + c_2 x \textit{\Large e}^{5x}

Ejemplo 3

Calcule la solución de la siguiente ecuación diferencial ordinaria lineal homogénea con coeficientes constantes

y'' + 4y' + 7y = 0

Empezamos escribiendo la ecuación auxiliar correspondiente a esta ecuación diferencial

m^2 + 4m + 7 = 0

Y aplicando el método del discriminante obtenemos que

m = \frac{-(4) \pm \sqrt{(4)^2-4(1)(7)}}{2(1)} = \frac{-4 \pm \sqrt{-12}}{2} = \frac{-4 \pm 2\sqrt{3}i}{2} = -2 \pm \sqrt{3}i

Por lo tanto, m_1= -2 + \sqrt{3}i y m_2= -2 - \sqrt{3}i son las raíces de este polinomio y así, la solución general es esta ecuación diferencial viene dada por

y = c_1 \textit{\Large e}^{-2x} cos(\sqrt{3}x) + c_2 \textit{\Large e}^{-2x} sen(\sqrt{3}x)

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ecuaciones Diferenciales Ordinarias lineales homogéneas con coeficientes constantes de n-ésimo orden

Habiendo estudiado el caso para ecuaciones diferenciales de segundo orden, veremos ahora que el caso para ecuaciones de mayor orden no será muy diferente pues simplemente generalizamos las ideas. Formalmente, al considerar una ecuación de la forma

a_{n} y^{(n)} + a_{n-1} y^{(n-1)} + \ldots + a_{1} y' + a_0 y = 0

Nuevamente consideraremos una función de la forma y=\textit{\Large e}^{mx} y al sustituirla en la ecuación, hacemos un desarrollo análogo al caso de segundo orden para obtener la siguiente ecuación

a_n m^n + a_{n-1} m^{n-1} + \ldots + a_1 m + a_0

Que nuevamente llamaremos ecuación auxiliar y, si esta tiene n soluciones distintas, entonces la solución general de la ecuación diferencial viene dada por

y = c_1 \textit{\Large e}^{m_1 x} + c_2 \textit{\Large e}^{m_2 x} + \ldots + c_n \textit{\Large e}^{m_n x}

Sin embargo, cuando no todas las n soluciones son iguales, debemos «combinar» los otros dos casos, de forma que si m_p tiene multiplicidad k, es decir, es una solución que se repite k veces, entonces la expresión

c_{p_1} \textit{\Large e}^{m_p x} + c_{p_2} x \textit{\Large e}^{m_p x} + c_{p_3} x^{2} \textit{\Large e}^{m_p x} + \ldots + c_{p_k} x^{k-1} \textit{\Large e}^{m_p x}

Se encuentra como una combinación lineal que forma parte de la solución.

Ejemplos

Ejemplo 4

Calcule la solución de la siguiente ecuación diferencial ordinaria lineal homogénea con coeficientes constantes

y''' + 3y'' - 4y = 0

Empezamos escribiendo la ecuación auxiliar correspondiente a esta ecuación diferencial

m^3 + 3m^2 - 4 = 0

Y aplicando el Método de Ruffini podemos hallar las raíces de este polinomio,

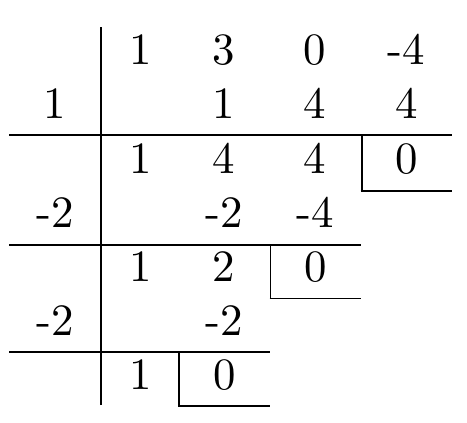
De esta forma, tenemos que m_1=1, m_2=-2 y m_3=-2. Notamos que -2 es una raíz multiplicidad dos, pues se repite dos veces. Así, la solución general es esta ecuación diferencial viene dada por

y = c_{1} \textit{\Large e}^{x} + c_{2} \textit{\Large e}^{-2x} + c_{3} x \textit{\Large e}^{-2x}

Ejemplo 5

Supongamos ahora que al plantear una ecuación diferencial ordinaria lineal homogénea con coeficientes constantes, su ecuación auxiliar se factoriza de la siguiente forma

(m-3)^2(m+7)^3(m-5)(m-(4+i9))(m-(4-i9))

Entonces, tomando en cuenta la multiplicidad de algunas raíces y que otras son complejas, la solución general es esta ecuación diferencial viene dada por

y =

c_1 \textit{\Large e}^{3x} + c_2 x \textit{\Large e}^{3x}

+ c_3 \textit{\Large e}^{-7x} + c_4 x \textit{\Large e}^{-7x} + c_5 x^2 \textit{\Large e}^{-7x}

+ c_6 \textit{\Large e}^{5x}

+ c_7 \textit{\Large e}^{4x} cos(9x) + c_8 \textit{\Large e}^{4x} sen(9x)

Ecuaciones Diferenciales Ordinarias Lineales Homogéneas con una solución conocida

Anthonny Arias-García1 comentario
  1. Introducción
  2. Reducción de Orden
    1. Ejemplos
      1. Ejemplo 1

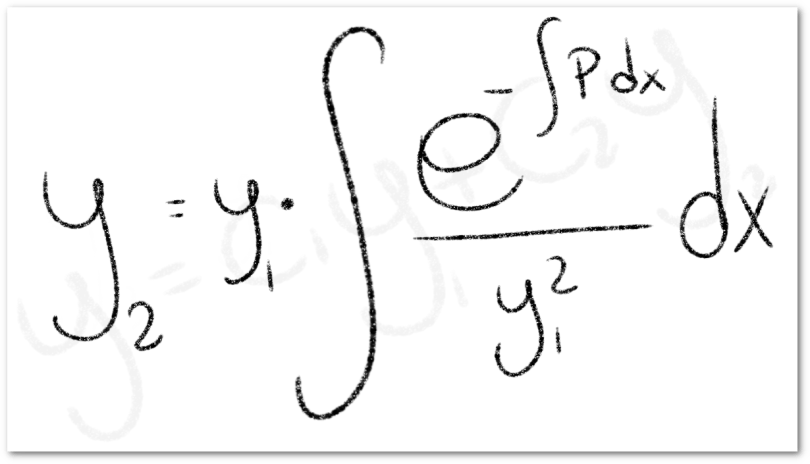
Veamos ahora el desarrollo de un método que nos permitirá reducir el orden de una ecuación diferencial ordinaria lineal homogénea una vez que hemos encontrado una de sus soluciones.

Diremos que una ecuación diferencial ordinaria lineal está expresada en su forma estándar si el coeficiente que multiplica a la derivada de mayor orden involucrada en la ecuación es exactamente igual a uno. Entonces, si consideramos una ecuación diferencial ordinaria lineal homogénea de segundo orden, diremos que esta está estandarizada si se encuentra expresada de la siguiente forma:

y'' + P(x) y' + Q(x) y = 0

Donde P(x) y Q(x) son funciones continuas en un intervalo I, pues de esta forma podemos garantizar que existe un conjunto fundamental de soluciones de esta ecuación en el intervalo I. Supongamos que y_1(x) es en efecto una solución conocida y que y_1(x) \neq 0 para todo x en el intervalo I.

También pudiera interesarte

Introducción

Partiremos del hecho de que al considerar una ecuación diferencial ordinaria lineal homogénea de segundo orden, existirá un conjunto fundamental de soluciones que consta de exactamente dos soluciones para esta ecuación.

Formalmente, si consideramos y_1 y y_2, dos soluciones linealmente independientes de una ecuación diferencial ordinaria homogénea de orden dos en un intervalo I, el principio de superposición para ecuaciones homogéneas establece que cualquier otra solución será combinación lineal de éstas, entonces la solución general estará definida en un intervalo I de la siguiente forma

y = c_1 y_1 + c_2 y_2

Nuestro propósito es encontrar una segunda solución y_2(x) tal que y_1(x) y y_2(x) son linealmente independientes, es decir, tal que y_2(x) \neq c_1 \cdot y_1(x). Consideramos entonces, una función auxiliar u(x) tal que y_2(x) = u(x) \cdot y_1(x).

La función y_2 debería satisfacer la ecuación y'' + P(x) y' + Q(x) y = 0, entonces, debemos calcular la primera y la segunda derivada de y_2 para posteriormente sustituirla en la ecuación.

y_2 = u \cdot y

y_2' = u \cdot y'_1 + y_1 \cdot u'

y_2'' = u \cdot y''_1 + 2 \cdot y'_1 \cdot u' + y_1 \cdot u''

Entonces al sustituir las funciones y_2, y_2' y y_2'' en la ecuación estandarizada, obtenemos

(u y''_1 + 2y'_1 u' + y_1 u'') + P (uy'_1 + y_1u') + Q (uy_1) = 0

Expandimos las expresiones distribuyendo P y posteriormente agrupamos los elementos que multiplican a u, u' y u''

u y''_1 + 2y'_1 u' + y_1 u'' + P uy'_1 + P y_1u' + Q uy_1 = 0

\Rightarrow \; y_1 u'' + 2y'_1 u' + P y_1u' + u y''_1 + P uy'_1 + Q uy_1 = 0

\Rightarrow \; y_1 u'' + (2y'_1 + P y_1 ) u' + (y''_1 + Py'_1 + Qy_1)u = 0

Debemos notar que al ser y_1 una solución de la ecuación, entonces y''_1 + Py'_1 + Qy_1 = 0, por lo tanto, tenemos que

y_1 u'' + (2y'_1 + P y_1 ) u' + (0)u = 0

\Rightarrow \; y_1 u'' + (2y'_1 + P y_1 ) u' = 0

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Reducción de Orden

Notemos que esta última ecuación involucra sólo la primera y segunda derivada de la variable u, entonces, si recurrimos a una nueva variable auxiliar w(x)=u'(x), podemos reducir el orden la ecuación diferencial como sigue

y_1 w' + (2y'_1 + P y_1 ) w = 0

Esta ecuación es precisamente una ecuación diferencial ordinaria de primer orden con variables separables, entonces podemos calcular su solución de la siguiente manera

\displaystyle y_1 w' + (2y'_1 + P y_1 ) w = 0

\displaystyle \Rightarrow \; y_1 w' = - (2y'_1 + P y_1 ) w

\displaystyle \Rightarrow \; \frac{w'}{w} = \frac{- (2y'_1 + P y_1 )}{y_1}

\displaystyle \Rightarrow \; \int \frac{w'}{w} = \int \frac{- (2y'_1 + P y_1 )}{y_1} dx

\displaystyle \Rightarrow \; \int \frac{w'}{w} dx = - \int \left( \frac{2y'_1}{y_1} + \frac{P y_1 }{y_1} \right) dx

\displaystyle \Rightarrow \; \ln(w) = - 2 \ln(y_1) - \int P dx + C

\displaystyle \Rightarrow \; \ln(w) + 2 \ln(y_1) = - \int P dx + C

\displaystyle \Rightarrow \; \ln(w) + \ln(y_1^2) = - \int P dx + C

\displaystyle \Rightarrow \; \ln(w y_1^2) = - \int P dx + C

\displaystyle \Rightarrow \; \textbf{\textit{\huge e}}^{\ln(w y_1^2)} = \textbf{\textit{\huge e}}^{- \int P dx + C}

\displaystyle \Rightarrow \; w y_1^2 = \textbf{\textit{\huge e}}^{- \int P dx + C}

Y considerando que w es una variable auxiliar, tenemos que

\displaystyle w y_1^2 = \textbf{\textit{\huge e}}^{\tiny - \int P dx + C}

\displaystyle \Rightarrow \; u' y_1^2 = \textbf{\textit{\huge e}}^{\tiny - \int P dx + C}

\displaystyle \Rightarrow \; u' = \frac{C_1 \textbf{\textit{\huge e}}^{\tiny - \int P dx}}{y_1^2}

\displaystyle \Rightarrow \; u = \int \frac{C_1 \textbf{\textit{\huge e}}^{\tiny - \int P dx}}{y_1^2} dx + C_2

Para simplificar esta última expresión, podemos escoger de forma conveniente los valores c_1=1 y c_2=0, y así, esta última expresión se convierte en

u = \displaystyle \int \frac{\textbf{\textit{\huge e}}^{\tiny - \int P dx}}{y_1^2} dx

Finalmente, como y_2(x) = u(x) \cdot y_1(x), entonces u(x) = \frac{y_2(x)}{y_1(x)}, de esta forma obtenemos

\displaystyle \frac{y_2(x)}{y_1(x)} = \int \frac{\textbf{\textit{\huge e}}^{\tiny - \int P dx}}{\left( y_1(x) \right)^2} dx \Rightarrow y_2(x) = y_1(x) \int \frac{\textbf{\textit{\huge e}}^{\tiny - \int P dx}}{ \left( y_1(x) \right)^2} dx

Esta última igualdad nos provee una fórmula para calcular una solución y_2 de una ecuación diferencial ordinaria lineal homogénea de segundo orden conociendo una solución particular y_1 y en consecuencia, la solución general de la ecuación. Veamos con algunos ejemplos como aplicar esta fórmula.

Si te ha parecido útil la información que hemos presentado en totumat y quieres ayudar a mantener este sitio en línea puedes mirar nuestros anuncios publicitarios o donar dinero a través de PayPal.

Ejemplos

Ejemplo 1

Calcule la solución general de la siguiente ecuación diferencial ordinaria lineal homogénea de segundo orden

x^2y'' - 3xy' + 4y = 0

en el intervalo (0,+\infty), sabiendo que y_1=x^2 es una solución particular de ésta.

Se verifica que en efecto es una solución de esta ecuación diferencial, pues si y=x^2, entonces

x^2(x^2)'' - 3x(x^2)' + 4(x^2) = x^2(2) - 3x(2x) + 4x^2 = 2x^2 - 6x^2 + 4x^2 = 0

Para hallar la otra solución particular, empezamos estandarizando la ecuación, en este caso dividimos cada sumando de la ecuación por x^2 para obtener

y'' - \frac{3}{x}y' + \frac{4}{x}y = 0

Así, identificando P(x)=\frac{3}{x} podemos calcular la otra solución de esta ecuación sustituyendo en la fórmula, obtenemos que

\displaystyle y_2(x) = x^2 \int \frac{\textbf{\textit{\huge e}}^{\tiny - \int \frac{3}{x} dx}}{(x^2)^2} dx = x^2 \int \frac{x^3}{(x^2)^2} dx = x^2 \ln(x)

De esta forma, contamos con las dos soluciones particulares y_1=x^2 y y_2(x) = x^2 \ln(x) y en consecuencia, podemos expresar la solución general de la ecuación, pues cualquier otra solución se expresa como combinación lineal de estas dos de la siguiente forma:

y(x) = c_1 x^2 + c_2 x^2 \ln(x)